Оценки разброса

Для оценки разброса значений вариационного ряда используются показатели размаха, отклонений и коэффициента вариации.

Размах вариациипредставляет собой разность между наибольшим и наименьшим значениями вариант.

Например, для таблицы 4 размах RсоставилR= 5 – 2,5 = 2,5 (балла). Для таблиц 5 и 6R= 5 – 2 = 3 (балла).

Среднее линейное отклонениепредставляет собой среднее арифметическое модулей отклонений вариант от своего среднего арифметического; рассчитывается по формуле:

Для примера из таблицы 5 d= (|2 – 4,02|*3 + |3 – 4,02|*25 + + |4 – 4,02|*39 + |5 – 4,02|*33)/100 = 0,6468 (балла), т.е. в среднем оценка студента отличается от среднего балла примерно на 0,6 балла.

Отметим, что если в этой формуле убрать знак модуля, то отклонения в разные стороны компенсируют друг друга, и результат окажется равным нулю (по соответствующему свойству среднего арифметического, аналогичного свойству математического ожидания).

Если вместо взятия по модулю возвести отклонение в квадрат, получим дисперсиювариационного ряда.

Для примера из таблицы 5 = 0,6996. Единицы измерения этой величины (баллы в квадрате) не имеют смысла, поэтому из нее извлекают корень квадратный и получаютсреднеквадратическое отклонение. В том же примере(балла). Столько составляет корень квадратный из среднего квадрата отклонения оценки каждого студента от среднего балла.

Свойства дисперсии для вариационного ряда аналогичны свойствам дисперсии в теории вероятностей. Для ее расчета можно вывести аналогичную формулу: .

Кроме того, если ряд состоит из нескольких отдельных групп наблюдений (пусть их число равно k), то его дисперсию можно рассчитать по следующей формуле:

где – средняя внутригрупповая дисперсия;

– дисперсияi-й группы;

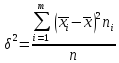-межгрупповая дисперсия.

Чтобы проиллюстрировать это правило, вернемся к примеру, в котором данные из таблицы 5 разбиты на две (k= 2) группы и представлены в таблицах 7 и 8.

Таблица 7– Оценки для специальности № 1

№	Балл (х)	Число студентов	х2
1	2	1	4
2	3	15	9
3	4	20	16
4	5	24	25
		n = 60	17,65

Рассчитаем групповую дисперсию для таблицы 7 по формуле = 17,65 – 4,12²= 0,7.

Таблица 8– Оценки для специальности № 2

№	Балл (х)	Число студентов	х2
1	2	2	4
2	3	10	9
3	4	19	16
4	5	9	25
		n = 40	15,675

Рассчитаем групповую дисперсию для таблицы 8 по формуле = 15,675 – 3,875²= 0,66.

Сведем расчеты в таблицу 9:

Таблица 8– Оценки для двух специальностей

Специальность	Число студентов	Средний балл	Дисперсия
№ 1	60	4,12	0,7
№ 2	40	3,875	0,66
		n = 40	15,675

Тогда межгрупповая дисперсия составит

((4,12 – 4,02)²*60 + (3,875 – 4,02)²*40)/100 = 0,01

Средняя внутригрупповых дисперсий составит

= (0,7*60 + 0,66*40)/100 = 0,68

Дисперсия всего вариационного ряда составит = 0,68 + + 0,01 = 0,69, что приблизительно совпадает с полученным ранее результатом. Незначительное расхождение объясняется погрешностью округления (при расчетах с помощью электронной таблицы совпадение получается точным).