Book2v1

31: + = 1/30;. Таким образом, при обнулении счетчика counter1 значение радиуса не уменьшается и далее продолжает рости.

Значение cRadius используется в строках 16 и 17 для формирования значения переменных координат nx и ny.

Листинг 46: Рисуем белый цветок на белом фоне

4smooth () ;

5 background (255) ;

6strokeWeight (1) ;

7}

8

9 float counter , counter1 ;

10float cx = 250;

11float cy = 250;

12float cRadius = 10;

13void draw () {

14stroke (0 , 50) ;

27counter = 0;

28}

29

33if ( counter1 > 2* PI ) {

34counter1 = 0;

35}

36}

37

101

В результате выполнения кода Листинга 46 мы получаем спиралевидное изображение, показанное на рисунке 56.

Рис. 56: Результат выполнения Листинга 46. Белый цветок на белом фоне.

Модифицируем код Листинга 46 так, как показано в Листинге 47. Изменение коснулось формирования значения счетчика counter1 в 32-й строке. Теперь значение счетчика зависит от горизонтального положения курсора мыши, таким образом мы добавили в наше приложение элемент интерактивного взаимодействия: пользователь может управлять свойствами отрисовки и получать результаты, как, например, на Рисунке 57.

Листинг 47: Рисуем симметрию на белом

102

7}

8

9 float counter , counter1 ;

10float cx = 250;

11float cy = 250;

12float cRadius = 100;

13

14void draw () {

15stroke (0 , 30) ;

29counter = 0;

30}

31

32 counter1 = counter1 + mouseX /(( float ) width *2) ;

33

34if ( counter1 > 2* PI ) {

35counter1 = 0;

36}

37}

Результат работы кода Листинга 47 показан на рисунке 57.

Задание 4. Измените код Листинга 46 так, чтобы вместо линий отрисовывались эллипсы разных оттенков и цветов.

Задание 5. Измените код Листинга 46 так, чтобы степень «закрученности» спирали зависела от положения курсора мыши на горизонтальной оси.

103

Рис. 57: Результат выполнения Листинга 47. Симметрия на белом.

В этом параграфе мы рассмотрели варианты работы с тригонометрическими функциями, разобрали примеры построения спиралей. В последующих главах мы еще вернемся к функциям синуса и косинуса для демонстрации интересных художественных решений с использованием синусоидальных траекторий движения.

7.2Кривые Безье

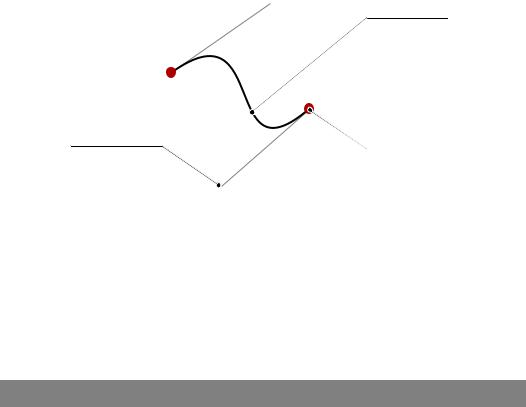
Кривые Безье часто используются в компьютерной графике: например, векторная графика (о которой мы еще будем говорить отдельно) активно использует их для описания геометрии. Математический аппарат кривых Безье мы рассматривать не будем, лишь взглянем на Рисунок ??. На нем можно увидеть, что кривая Безье состоит из опорных точек и кривой (путем). В Processing опорные точки для упрощения разделили на якоря (anchors), через которые кривая проходит, и контрольные точки (control points), которые задают форму кривой. На Рисунке 58 видно, что кривая начинается в якоре А и стремиться к якорю B, аформа кривой задается положением контрольных точек C и D.

В редакторах растровой графики всегда есть схожие элементы управления визуальной настройкой кривой Безье. В Processing нам придется указывать координаты для каждой опорной точки, т.е. 8 цифр.

Рассмотрим пример отрисовки кривой Безье. В коде Листинга 48 отрисовываем кривую Безье в 23-й строке с помощью вызова метода bezier(). Этот метод принимает 8 аргументов. Первые два аргумента –

104

D

Рис. 58: Визуализация кривой Безье с опорными точками.

это X и Y координаты первой якорной точки, вторая пара X и Y – координаты первой контрольной точки, третья пара, соответственно, – вторая контрольная точка и, наконец, четвертая пара аргументов – координаты второй якорной точки.

Листинг 48: Управляем опорными точками кривой Безье

1void setup () {

3smooth () ;

4}

5

6void draw () {

7 background (255) ;

8stroke (100) ;

9strokeWeight (5) ;

10

11float anc1X = mouseX ;

12float anc1Y = mouseY ;

20noFill () ;

21bezier ( anc1X , anc1Y , cont1X , cont1Y , cont2X , cont2Y , anc2X ,

anc2Y );

105

22

23stroke (50) ;

24strokeWeight (1) ;

25line ( anc1X , anc1Y , cont1X , cont1Y );

26line ( anc2X , anc2Y , cont2X , cont2Y );

27

28fill (150) ;

29noStroke () ;

30rectMode ( CENTER );

31rect ( cont1X , cont1Y , 6 ,6) ;

32rect ( cont2X , cont2Y , 6 ,6) ;

33

34fill (170 ,0 ,0) ;

35noStroke () ;

36ellipseMode ( CENTER );

37ellipse ( anc1X , anc1Y ,10 ,10) ;

38ellipse ( anc2X , anc2Y ,10 ,10) ;

39}

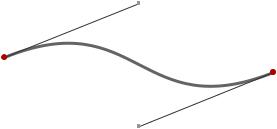
Координаты опорных точек мы определяем в строках с 11-й по 18-ю. Первый якорь будет располагаться в месте курсора мыши, второй якорь будет зеркально отражен (см. строку 17 и 18) по горизонтали и вертикали. Контрольные точки будут зафиксированы в центре по горизонтали и равноудалены от центральной горизонтальной оси. Кроме отрисовки самойсобственно кривой (пути), мы отрисуем и опорные точки, и управляющие линии. Результат работы кода Листинга 48 можно увидеть на Рисунке 59.

Рис. 59: Результат выполнения Листинга 48. Управление опорными точками кривой Безье.

106

http://www.openprocessing.org/sketch/159891), который разработал приложение и опубликовал исходные коды под открытой лицензией. Кривые Безье в коде Листинга 49 слагают симметричный ансамбль формы.

Листинг 49: http://www.openprocessing.org/sketch/159891

1

2 float num , pathR , pathG , pathB ;

3

4void setup () {

6}

7

8void draw () {

9fill (0 , 30) ;

29stroke ( pathR , pathG , pathB , 50) ;

30fill ( pathR , pathG , pathB , 30) ;

33}

34num += 0.01;

35}

Результат работы кода Листинга 49 показан на Рисунке 60.

В коде Листинга 49 за каждый вызов метода draw() происходит отрисовка 180 (360 c шагом 2) кривых Безье в цикле for (см. строку 17).

107

Кривая Безье строится по двум якорным точками, координаты которых определяются в 19-й – 20-й и 22-й – 23-й строках соответственно. В вычислении координат участвует свойство num, которое определено во 2-й строке и увеличивается на 0.01 в 34-й строке с каждым вызовом метода draw(). Таким образом происходит не только синусоидальное изменение координат из-за переменной i, но и изменение угла (строка 18).

Рис. 60: Результат выполнения Листинга 49.

Изменение цвета кривых и заливки происходит в строках 25–27. Значения трех цветовых каналов меняются также в зависимости от переменной num. Изменения каналов происходят со сдвигом на PI, TWO_PI и HALF_PI.

Одной из вариаций на тему этого кода является следующий пример: Михаэль Пинн опубликовал его так же под открытой лицензией (Michael Pinn, http://www.openprocessing.org/sketch/160305).

Листинг 50: http://www.openprocessing.org/sketch/160305

7}

8

9void draw () {

10fill (0 , 40) ;

11rect ( -1 , -1, width +1 , height +1) ;

108

27ellipse (x2 , y2 , 5, 5) ;

28}

29num += 0.5;

30}

Результат работы кода Листинга 50 показан на Рисунке 61. В этой работе нет изменения цвета. В отличие от предыдущего кода, здесь отрисовываются две кривые Безье (строки 23 и 24) и эллипсы (строки 26 и 27).

Рис. 61: Результат выполнения Листинга 50.

Первый эллипс (строка 26) отрисовывается в координатах первой якорной точки кривой Безье (строка 23), второй эллипс – во второй. Причем якорные точки обеих кривых совпадают на координатной плоскости, однако положение контрольных точек симметрично.

109

Задание 6. Измените код Листинга 47 так, чтобы вместо линий отрисовывались кривые Безье.

Можно отметить, что плавность линий и изящество построений кривых Безье расширяют возможности создания простых геометрических фигур. Конечно, кривые Безье требуют много параметров: необходимо думать о расположении якорей и контрольных точек. Тем не менее эти кривые – уникальное средство в руках цифрового художника. Мы будем использовать кривые Безье в дальнейшем, так что у вас еще появится возможность увидеть их «в действии».

В этой главе мы рассмотрели применение тригонометрических функций и работу с кривыми Безье в Processing. Удобство использования этих функций и кривых позволяет включать их в работу на любом этапе. Особенно интересным представляется использование их для отрисовки не собственно линий, а путей, по которым будут отрисовываться объекты и формироваться художественные произведения. Фундаментальному вопросу о том, какие вообще объекты могут отрисовываться на ваших полотнах будет посвящена следующая глава.

110