4.1. Приведённые инерционные параметры

Приведённые инерционные параметры расчитываются из условия сохранения киннетических энергий инерционных масс действительной динамической системы и преденной динамической модели.

=++++++

- Потенциальная энергия действительной динамической системы

- Потенциальная энергия приведенной динамической системы

=+++

=

- потенциальная энергия приведенной ременной системы

=

=

=

=+++

=×=(i)²

===72,327·14²=2,835·

=·(i)=2,835··2²=1,134·

=*()²=6,921··2²=2,768·кг·см/рад

==6,351·кг·см/рад

=*(i)²=6,351··1²=6,351·

5. Математическое описание приведенной динамической модели

Для вывода математической модели используем прямой метод. Прямой метод заключается в отделении инерционных масс от упругого скелета уравнения равновесия динамической модели и составления для каждой из них уравнения равновесия всех обобщенных сил, действующих на них. Вследствие этого обобщенная движущая сила, приложенная к каждой массе со стороны ее входа, затрачивается на преодоление силы сопротивления, действующей со стороны входа, а также инерционной силы, развивающейся при колебательном движении этой массы. J

1 масса

2 масса

3 масса

4 масса

5 масса

Запишем колебания ПДМ в виде системы линейных неоднородных дифференциальных уравнений второго порядка:

(1)

Перейдем к относительным обобщенным координатам для минимального количества степеней свободы:

(2)

Разделим каждое уравнение системы (1) на коэффициент, стоящий перед производной второго порядка, с учетом (2) получим:

(3)

Вычитая попарно уравнения системы (3) получим:

(4)

Решение системы (4) складывается из решения системы однородных уравнений и частных решений, соответствующих правым частям дифференциальных уравнений данной системы.

В итоге уменьшилось число дифференциальных уравнений, следовательно, систему легче решать. Теперь число дифференциальных уравнений точно соответствует числу степеней свободы.

Запишем однородную систему в виде:

(4)

6. Исследование системы линейных уравнений

Исследуем систему однородных дифференциальных уравнений(4):

(4)

Представим приведенную модель (4) в виде двух массовых парциальных контуров:

Рис.6.1. Парциальные контуры

парциальные частоты парциальных контуров

коэффициенты связей инерционных масс в парциальных системах

Введем обозначения:

(5)

(6)

Запишем систему (4) с учётом (5):

(7)

Приведём выражение всех коэффициентов в системе (7) к однородному виду, введя обозначение:

(8)

Запишем систему (7) с учётом (8) и получим:

(9)

Найдём решение системы уравнений (9), введя обозначения:

(10)

- неизвестная амплитуда колебаний на определённой частоте;

k- собственная частота колебний.

Найдём вторую производную обозначений системы (10). Она примет вид:

(11)

Подставим (10) и (11) в (9) и получим:

(12)

Для нахождения собственных частот составим частотный определитель

Раскроем частотный определитель в следующем виде:

(13)

- миноры соответствующих элементов первой строки частотного определителя.

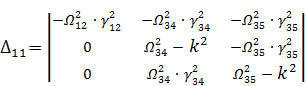
С учётом (13) получим частотное уравнение в аналитическом виде:

Вычислим значения парциальных частот и коэффициентов связей инерционных масс между парциальными контурами:

Вычислим коэффициенты частотного уравнения:

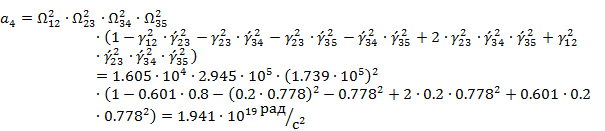
Обозначим:

В итоге получим уравнение 4-й степени:

Сократим уравнение на общий член 10²⁰. В итоге получим:

Найдем корни уравнения с помощью метода последовательного перебора предполагаемых значений от 0 до значений, при котором Так как уравнений 4-й степени, следовательно, процесс перебора произведём 4 раза:

p₁=0.064

p₂=0.386

p₃=1.823

p₄=4.34

Проверка:

p₁+p₂+p₃+p₄=a₁=6.583

p₁∙p₂∙p₃∙p₄=a₄=0.194

Так как

Следовательно,

Рисунок 6.2. Значения угловых частот, парциальных частот и собственных частот колебаний валов

В системе (21) количество уравнений 5, а неизвестных форм колебаний 4, следовательно, одно уравнение можно не использовать для нахождения коэффициентов. Целесообразно не использовать самое сложное уравнение, а применить его для проверки полученных результатов.

Выразим из 1-го, 2-го, 4-го и 5-го уравнений системы (21) коэффициенты :

Рассчитаем значения коэффициентов форм собственных колебаний на каждой частоте:

Первая форма собственных колебаний:

Вторая форма собственных колебаний:

;

3. Третья форма собственных колебаний.

4. Четвертая форма собственных колебаний

Рисунок 7.3. Формы крутильных колебаний

ВЫВОДЫ

В данной курсовой работе был произведен динамический расчет привода ротационной печатной машины. В качестве расчета была выбрана линейная динамическая система, в которой все рабочие органы совершают свое вращательное движение с постоянной скоростью.

В задании были указаны основные параметры элементов привода. На основе их численных значений были рассчитаны основные силовые и скоростные параметры. Затем были определены основные геометрические параметры основных элементов привода.

Затем были выбраны основные инерционные массы и упругие участки. Для них были рассчитаны инерционные моменты и жесткости.

Шкивы, цилиндры имеют сложную форму, следовательно, моменты инерции и жесткости для них рассчитывались как сумма значений элементарных деталей, соединенных последовательно.

Для динамической системы была составлена приведенная динамическая модель, где не учитываются зазоры в зубчатых передачах, нелинейные факторы в зоне печатного контакта печатной пары печатной секции.

Приведение заключалось в выборе звена приведения и выравнивания скоростей всех остальных звеньев относительно скорости звена приведения. Следовательно, возникла необходимость корректировки инерционных и жесткостных параметров производился из условия равенства кинематической и потенциальных энергий действительной и приведенной систем.

Для вывода дифференциальных уравнений, описывающих крутильные колебания динамической модели, применялся прямой метод.

После составления системы дифференциальных уравнений необходимо было ее исследовать. Исследовалась система в виде однородных уравнений. Система была представлена в виде 2-хмассовых парциальных контуров.

Для нахождения собственных частот решение искалось в виде

В итоге получили систему дифференциальных уравнений относительно неизвестных частот . Из этой системы был составлен частотный определитель. Затем было составлено частотное уравнение в аналитическом виде. Каждый корень данного уравнения равен квадрату собственных частот. Корни уравнения определялись методом последовательного перебора параметра частотного уравнения, при котором значение полинома равно 0.

В результате были получены 4 собственные частоты крутильных колебаний и для каждой из них найдены формы собственных колебаний и построены эпюры на каждой собственной частоте.

Анализируя полученные графики форм собственных колебаний можно сделать выводы:

- на 1-й форме колебаний инерционные массы колеблются незначительно, интенсивности колебаний каждой массы почти одинаковы;

- на 2-й форме колебаний массы колеблются интенсивнее, но с небольшой разницей в амплитудных значениях;

- на 3-1 форме колебания интенсивны и с большими амплитудными значениями;

- на 4-й форме самые значительные по интенсивности колебания. Необходимо рассчитать ведущий вал на прочность и долговечность.

Также из графиков можно сделать вывод, что ни одна узловая точка эпюр форм собственных колебаний не проходит через инерционные массы, содержащие зубчатые передачи, муфты с зазором и т.п., иначе это могло привести к раскрытию зазоров.

В итоге, в данной работе мы ознакомились с необходимым набором методик исследования динамических систем в весьма удобном и оригинальном виде.