Практикум №2

Практикум №2

Условные вероятности. Независимые события.

1. На клавиатуре компьютера 105 клавиш. Найдите вероятность того, что обезьяна, нажав поочередно 2 клавиши случайным образом, напишет слово «ОЙ».

2. Случайным образом выбираем натуральное число от 1 до 20. Являются ли события

А={ число четное} и B={ выбранное число делится на 5} независимыми?

3. Из колоды в 36 карт одну за другой вытаскивают 2 карты. Какова вероятность, что среди них 2 туза?

4. Автомат заряжен пятью патронами, два из которых холостые. Производится 2 выстрела. Какова вероятность того, что оба они будут холостые?

5. Случайным образом выбираем натуральное число от 1 до 25. Какова вероятность извлечь нечетное число, если известно, что выбранное число делится на 5.

6. Вероятность того, что при одном измерении некоторой физ. величины будет допущена ошибка, превышающая заданную точность, = 0,4. Произведены 3 независимых измерения. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность.

Формула полной вероятности. Формула Байеса.

1. Задача о туристе

2. В первом ящике 3 белых и 8 красных шаров, во втором 6 белых и 5 красных. Из первого во второй наудачу переложили один шар. Какова теперь вероятность вынуть из первого ящика черный шар?

3. Из 40 экзаменационных билетов студент выучил только 30. Каким выгоднее ему зайти на экзамен: первым или вторым?

4. С двух метеостанций в телецентр поступают сообщения о прогнозе погоды на завтра. Вероятность ошибочного прогноза для 1-й метеостанции равна 0,25, а для второй - 0,3. В телецентре с вероятностью 0,6 выбирают сообщение с 1-й метеостанции и с вероятностью 0,4 -со 2-й метеостанции и передают его по телевидению. Какова вероятность того, что переданный по TV прогноз будет ошибочным?

Ответ: 0,27

5. В условиях зад. 3 переданный по TV прогноз оказался ошибочным. Какова вероятность того, что он поступил с 1-й метеостанции?

Ответ: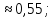

6. В некоторой местности 20% дней в году – дождливые и 80% - солнечные. Прогноз погоды дают два предсказателя. Первый ошибается в 30% случаев, 33 второй – в 10%. Первый утверждает, что завтра будет солнце, второй – что дождь. Чей прогноз сбудется с большей вероятностью?

Указание

Примените формулу Байеса, считая гипотезами солнечную или дождливую погоду на завтрашний день, а событием А – выданные прогнозы.

Решение

Пусть гипотеза Н1 заключается в том, что в выбранный день будет солнечная погода, а гипотеза Н2 – дождливая. Тогда при реализации первой гипотезы прогноз первого предсказателя верен, а второго – ошибочен, а при реализации второй гипотезы – наоборот.

Найдем полную вероятность события А (выдачи соответствующих прогнозов):

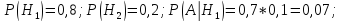
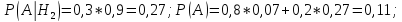
Итак, вероятность получения именно таких взаимоисключающих прогнозов равна 0,11. Переоценим вероятность первой гипотезы, зная, что событие А произошло. Если она окажется больше 0,5, то с большей вероятностью сбудется прогноз первого предсказателя, если меньше 0,5 – прогноз второго.

более вероятно, что сбудется прогноз первого предсказателя.

Ответ: прогноз первого.

Схема Бернулли.

1. Игральную кость бросают 7 раз. Какова вероятность того, что

1. « 6» выпадет 5 раз. Найти наивероятнейшее число выпадений « 6»;

2. число 3 выпадет 2 раза;

3. « 1» ни разу не выпадет.

2. На данной остановке данным маршрутом автобуса пользуются 20 человек, причем каждый из них, независимо от остальных, опаздывает с Р=1/7. Чему равно наиболее вероятное число пассажиров, заполняющих автобус на данной остановке.

3. Производится четыре независимых выстрела по цели. Вероятность попадания в цель при каждом выстреле равна 0.5. Для разрушения цели достаточно хотя бы одного попадания. Найти вероятность того, что цель будет разрушена.

4. Вероятность выхода из строя одного элемента в течение года равна 0,2. Какова вероятность того, что из 100 элементов в течение года выйдут из строя

а) 15 элементов?

2. От 10 до 20 элементов?

5. Вероятность прерывания телефонного соединения равна 0,03. Какова вероятность того, что среди 200 соединений будет не более двух прерываний?

6. В городе работают 10 коммерческих банков. Для каждого из них вероятность банкротства в течение года равна 0.1. Найдите вероятность того, что в течение года в данном городе количество обанкротившихся банков не превысит число 1.

Домашнее задание.

1. Подбрасывается игральная кость. Зависимы или нет события А= { появление четного числа } и В={ появление числа, большего 3 }?

2. Компьютерная фирма использует дисководы двух производителей. Для 1-го производителя вероятность выпуска бракованного дисковода равна 0,05, для 2-го – 0,02. Найти вероятность установки бракованного дисковода, если известно, что фирма закупила 200 дисководов 1-го производителя и 300 - 2-го производителя.

Ответ: 0,032

3. Используем условие зад. № 2 и поставим вопрос так: если установленный дисковод оказался бракованным, то какова вероятность того, что он поступил от 1-го производителя?

Ответ: 5/8

4. Один игрок бросает 6 игральных костей и выигрывает, если выпадет хотя бы одна « 6». А другой бросает 12 игральных костей и выигрывает, если выпадут хотя бы две « 6». У кого больше шансов выиграть?

5. Пассажир может обратиться за получением билета в одну из трёх касс (А,B,C). Вероятности обращения в каждую кассу зависят от их местонахождения и равны соответственно 0,4; 0,5 и 0,1. Вероятности того, что к моменту прихода пассажира, имеющиеся в кассе билеты распроданы равны соответственно 0,4; 0,3 и 0,1. Найдите вероятность того, что билет куплен. В какой из касс это могло произойти с наибольшей вероятностью?