Двухпроводная линия передачи (длинная линия)_2015_fin
.doc
Лабораторная работа
«Двухпроводная линия передачи (длинная линия)»
|
|
|
Рис. 1. Двухпроводная линия передачи. |
|
|
|
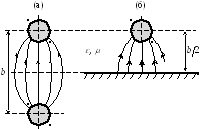
Рис. 2. Симметричная (а) и несимметричная (б) линии передачи. |
|
|
|
Рис. 3. Схема лабораторного макета длинной линии. |
В
лаборатории ничего похожего на Рис. 1
вы не увидите, т.к. растянуть достаточно
однородную линию длиной порядка 100 м
(такая длина железной линии необходима
для получения значимых эффектов, медная
линия должна быть в разы длиннее) нет
возможности. Поэтому, во-первых макет
реализован в виде так называемой
несимметричной линии. Несимметричная
линия («половина» от обычной) представляет
собой один провод, расположенный над
плоским проводящим экраном на расстоянии
![]() от него (Рис. 2). Если экран можно
считать идеально проводящим и бесконечным
(мы так и будем делать), то такая
несимметричная линия будет эквивалентна
симметричной (электрическое и магнитное
поля в верхних полупространствах будут
одинаковы).
от него (Рис. 2). Если экран можно
считать идеально проводящим и бесконечным
(мы так и будем делать), то такая
несимметричная линия будет эквивалентна
симметричной (электрическое и магнитное
поля в верхних полупространствах будут
одинаковы).
Во-вторых,
несимметричная линия для уменьшения
габаритов свернута в спираль на жестком
цилиндрическом каркасе длиной порядка
метра (Рис. 3). Заданное расстояние
между проводником и экраном (фольга)
поддерживается за счет диэлектрической
прокладки (полиэтилен) толщиной
![]() с
с
![]() .
Для подключения к линии на дискретных
расстояниях предусмотрен специальный
зонд.
Если
шаг намотки спирали много больше
.
Для подключения к линии на дискретных
расстояниях предусмотрен специальный
зонд.
Если
шаг намотки спирали много больше
![]() (это так и есть) и длина витка (порядка
1 м) не близка к длине волны (это не
так только на частотах порядка 200 МГц,
которые мы не используем), то взаимодействие
витков спирали можно не учитывать. В
целом, как показывает детальное
рассмотрение (которое здесь не приводится),
несмотря на отмеченные особенности
нашей установки, процессы распространения
волн в этом макете будут происходить
так же, как и в классической двухпроводной
линии, изображенной на Рис. 1.
(это так и есть) и длина витка (порядка
1 м) не близка к длине волны (это не
так только на частотах порядка 200 МГц,
которые мы не используем), то взаимодействие
витков спирали можно не учитывать. В
целом, как показывает детальное
рассмотрение (которое здесь не приводится),
несмотря на отмеченные особенности
нашей установки, процессы распространения
волн в этом макете будут происходить
так же, как и в классической двухпроводной
линии, изображенной на Рис. 1.
|
|
|
Рис. 4.
Эквивалентная
схема участка двухпроводной линии
длиной
|
![]() ,
,
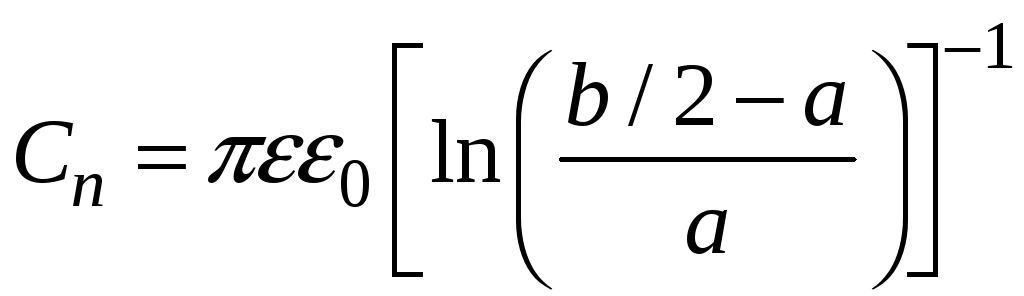 ,
,
![]() ,
,
![]() .
.
Здесь
![]() и
и
![]() – электрическая и магнитная постоянные.
– электрическая и магнитная постоянные.
Если
указанные 4 параметра известны, то ток
![]() и напряжение
и напряжение
![]() описываются системой так называемых
телеграфных уравнений. Они могут быть
выведены непосредственно из уравнений
Максвелла (при условии малости поперечных
размеров линии по сравнению с длиной
волны
описываются системой так называемых
телеграфных уравнений. Они могут быть
выведены непосредственно из уравнений
Максвелла (при условии малости поперечных
размеров линии по сравнению с длиной
волны
![]() ),
либо из рассмотрения эквивалентной
схемы, изображенной на Рис. 4. Телеграфные
уравнения имеют следующий вид:
),
либо из рассмотрения эквивалентной
схемы, изображенной на Рис. 4. Телеграфные
уравнения имеют следующий вид:
![]() ,
,
![]() .
.
Отметим,
что при отсутствии потерь (![]() ,
,
![]() )
система сводится к волновому уравнению,
решениями которого являются волновые
возмущения, распространяющиеся вдоль
линии в обе стороны со скоростью
)
система сводится к волновому уравнению,
решениями которого являются волновые
возмущения, распространяющиеся вдоль
линии в обе стороны со скоростью
![]() без искажения формы.
без искажения формы.
Для
гармонических процессов, когда
![]() и
и
![]() ,
из получим одномерные уравнения
Гельмгольца
,
из получим одномерные уравнения
Гельмгольца
![]() ,
,
![]() ,
,
где
![]() – постоянная распространения,
– постоянная распространения,
![]() – постоянная затухания,
– постоянная затухания,
![]() – волновое число. Уравнения легко
решаются, и для напряжения и тока получаем
– волновое число. Уравнения легко
решаются, и для напряжения и тока получаем
![]() ,
,
![]() ,
,
|
|
|
Рис. 5.
Схема
подключения двухпроводной линии
длиной
|
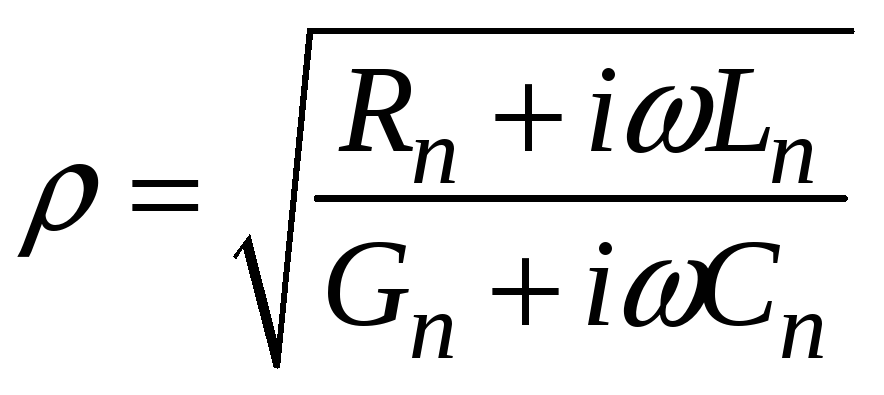 называется волновым сопротивлением
линии. Для линии без потерь
называется волновым сопротивлением
линии. Для линии без потерь
На
Рис. 5 приведена используемая в работе
схема возбуждения линии длиной
![]() .
Волну, бегущую от генератора (с
коэффициентом
.
Волну, бегущую от генератора (с
коэффициентом
![]() ,
определяемым напряжением генератора
,
определяемым напряжением генератора
![]() и его внутренним сопротивлением
и его внутренним сопротивлением
![]() ),
называют прямой или падающей. Другую
волну называют отраженной, в данном
случае она возникает из-за наличия
нагрузки
),
называют прямой или падающей. Другую
волну называют отраженной, в данном
случае она возникает из-за наличия
нагрузки
![]() (также отраженная волна возникает на
других неоднородностях: открытый конец
линии, изгибы, разветвления, изменения
размеров
(также отраженная волна возникает на
других неоднородностях: открытый конец
линии, изгибы, разветвления, изменения
размеров
![]() или
или
![]() ).
Коэффициент
).
Коэффициент
![]() при отраженной волне можно найти и
записать в виде
при отраженной волне можно найти и
записать в виде
![]() ,
где
,
где
![]() .
.
Величина
![]() называется коэффициентом отражения от
нагрузки. Выбирая нагрузку
называется коэффициентом отражения от
нагрузки. Выбирая нагрузку
![]() получаем
получаем
![]() ,
отраженная волна отсутствует, в линии
остается только прямая волна
,
отраженная волна отсутствует, в линии
остается только прямая волна
![]() .
Отсюда можно получить комплексный
коэффициент передачи отрезка линии
длиной
.
Отсюда можно получить комплексный
коэффициент передачи отрезка линии
длиной
![]() :
:
![]() .
.
Как
показывают расчеты величины
![]() ,
отрезок двухпроводной линии является
фильтром нижних частот с частотой
отсечки в районе 1 МГц для значений
,
отрезок двухпроводной линии является
фильтром нижних частот с частотой
отсечки в районе 1 МГц для значений
![]() порядка десятков метров. С увеличением
длины отрезка частота отсечки уменьшается.
порядка десятков метров. С увеличением
длины отрезка частота отсечки уменьшается.
Задания и указания.
1.
Понятие длинной линии.
Постройте график зависимости
![]() (взять
(взять
![]() ,
,
![]() )
от
)
от
![]() в диапазоне 100 Гц – 10 МГц (в
логарифмическом масштабе как по
в диапазоне 100 Гц – 10 МГц (в
логарифмическом масштабе как по
![]() ,
так и по
,
так и по
![]() ).
Укажите, на каких частотах лабораторный
макет является длинной линией.
).
Укажите, на каких частотах лабораторный
макет является длинной линией.
2.
Согласование линии. Вычислите
волновое сопротивление линии без потерь
![]()
![]() .
Помните, что
.
Помните, что
![]() – расстояние от центра провода до
экрана. Детально изучите клеммы макета
(см. Рис. 6) и соберите схему согласно
Рис. 5. Подключайте «землю» приборов
к «земле» линии. Предварительно с помощью
омметра установите сопротивление
нагрузки
– расстояние от центра провода до
экрана. Детально изучите клеммы макета
(см. Рис. 6) и соберите схему согласно
Рис. 5. Подключайте «землю» приборов
к «земле» линии. Предварительно с помощью
омметра установите сопротивление
нагрузки
![]() (переменного резистора) максимально
близкое к
(переменного резистора) максимально
близкое к
![]() .
.
|
|
|
Рис. 6. Вид макета сверху, расположение и назначение клемм. |
3.
Исследование частотных характеристик
линии. Подключите
параллельно нагрузке осциллограф (в
режиме внутренней синхронизации) и
измерьте зависимость
![]() в диапазоне 100 Гц – 200 кГц для полной
линии. Далее переключите осциллограф
на зонд и измерьте ту же зависимость
для двух отрезков линии меньшей длины
(например, 88 м и 65 м). Контролируйте
постоянство амплитуды сигнала на входе
линии, подав входной сигнал на второй
луч осциллографа. Спад до нуля увидеть
не удастся, но начало этого спада должно
быть видно. Если удастся, определите
частоту отсечки по уровню
в диапазоне 100 Гц – 200 кГц для полной
линии. Далее переключите осциллограф
на зонд и измерьте ту же зависимость
для двух отрезков линии меньшей длины
(например, 88 м и 65 м). Контролируйте
постоянство амплитуды сигнала на входе
линии, подав входной сигнал на второй
луч осциллографа. Спад до нуля увидеть
не удастся, но начало этого спада должно
быть видно. Если удастся, определите
частоту отсечки по уровню
![]() .
На каждой кривой напишите значение
.
На каждой кривой напишите значение
![]() и вычислите максимальное ослабление в
Дб по формуле
и вычислите максимальное ослабление в
Дб по формуле
![]() .
.
4.
Исследование ослабления и запаздывания
импульсных сигналов. Отключите
от входа линии звуковой генератор и
подключите туда генератор прямоугольных
импульсов. Длительность импульса
![]() выберите пол микросекунды (
выберите пол микросекунды (![]() ).
Используя известный результат, что
спектр такого импульса пропорционален
величине
).
Используя известный результат, что
спектр такого импульса пропорционален
величине
![]() ,
вычислите частоту
,
вычислите частоту
![]() первого нуля спектра и ее примите за
ширину спектра.
первого нуля спектра и ее примите за
ширину спектра.
На один луч осциллографа подайте сигнал со входа линии, на второй – с нагрузки. Осциллограф переведите в режим синхронизации по внешнему импульсу, а этот импульс подайте на осциллограф со специального выхода генератора прямоугольных импульсов. В результате вы должны увидеть два импульса, входной и прошедший через линию. С помощью вольтметров осциллографа измерьте отношение амплитуд в максимуме (ослабление) и выразите его в Дб.
Измерьте
запаздывание прошедшего импульса (в
![]() ).
Имейте в виду, что форма импульса очень
сильно искажается. Если на входе импульс
еще похож на прямоугольный, то после
прохождения отрезка линии его фронты
существенно сглаживаются. Поэтому
необходимо привязаться к какой-то
характерной точке, которую можно
идентифицировать как на исходном
импульсе, так и на пропущенном через
линию. Например, это может быть точка
максимума, тогда запаздывание импульса
будет определяться запаздыванием его
максимума. Возможны и другие варианты,
например привязка к фиксированному
уровню сигнала (относительно максимума)
на переднем или заднем фронте.
).
Имейте в виду, что форма импульса очень
сильно искажается. Если на входе импульс
еще похож на прямоугольный, то после
прохождения отрезка линии его фронты
существенно сглаживаются. Поэтому
необходимо привязаться к какой-то
характерной точке, которую можно
идентифицировать как на исходном
импульсе, так и на пропущенном через
линию. Например, это может быть точка
максимума, тогда запаздывание импульса
будет определяться запаздыванием его
максимума. Возможны и другие варианты,
например привязка к фиксированному
уровню сигнала (относительно максимума)
на переднем или заднем фронте.
Измерьте время нарастания (от нуля до максимума) и время спада (от максимума до нуля) для входного и прошедшего импульсов, вычислите отношения этих времен (они характеризуют степень расплывания фронтов).
Теперь
проделайте те же измерения (ослабление,
запаздывание, размытие фронтов) для
двух меньших длин линии (например, 88 м
и 65 м), подав на второй луч осциллографа
сигнал с зонда. По трем точкам постройте
графики зависимости ослабления,
запаздывания, и отношения времен размытия
фронтов от длины линии. Вычислите
скорость распространения импульса
(групповую скорость), соотнесите ее с
![]() .
.
После
этого установите длительность импульса
![]() ,
определите ширину спектра, снова измерьте
ослабление, запаздывание и размытие
фронтов для трех длин линии (108 м и,
например, 88 м и 65 м), постройте
графики и вычислите групповую скорость.
,
определите ширину спектра, снова измерьте
ослабление, запаздывание и размытие
фронтов для трех длин линии (108 м и,
например, 88 м и 65 м), постройте
графики и вычислите групповую скорость.
5.
Исследование отраженного сигнала.
Разомкните
линию (отключите нагрузку), подключите
зонд примерно в середину линии (например,
66 м) и подайте сигнал с него на
осциллограф. Вы должны увидеть основной
импульс и через доли
![]() – отраженный от конца линии импульс.
По времени задержки и пройденному пути
(у вас есть график) убедитесь, что это
действительно отраженный от конца линии
импульс. Подключите назад нагрузку и
наблюдайте исчезновение отраженного
импульса. Варьируйте сопротивление
нагрузки и наблюдайте изменения в
амплитуде отраженного импульса.
– отраженный от конца линии импульс.
По времени задержки и пройденному пути
(у вас есть график) убедитесь, что это
действительно отраженный от конца линии
импульс. Подключите назад нагрузку и
наблюдайте исчезновение отраженного
импульса. Варьируйте сопротивление
нагрузки и наблюдайте изменения в
амплитуде отраженного импульса.
1 Столяров О.И., Яневич Ю.М. Распространение и формирование сигналов в линиях передачи. Учебное пособие. СПб, 2004 (есть в библиотеке).