Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Literatura / Книга18_МОСТУ_АМПС_ПослВерстка / Главы_6_10.doc

Скачиваний:

113

Добавлен:

21.03.2016

Размер:

2.54 Mб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

6. Функции от матриц. Матричная экспонента и ее свойства. Кронекеровские матричные структуры

Рассматривается – квадратная матрицаA, на которой конструируются функции от матрицы трех типов:скалярная функция от матрицы, векторная функция от матрицы и матричная функция от матрицы.

Определение 6.1 (О6.1). Скалярной функцией (СФМ) от квадратной матрицы A называется функция , которая реализует отображение:Rⁿ^×ⁿR, где R – множество действительных чисел.

Примерами скалярных функций от матрицы явля-ются:– детерми-нант, след, число обусловленности и норма матрицы соответственно, СФМ является квадратичная форма .

Определение 6.2 (О6.2). Векторной функцией от квадратной матрицы A называется функция , которая реализует отображение :Rⁿ^×ⁿRⁿ, где Rⁿ – n-мерное действительное пространство.

Примерами векторных функций от матрицы (ВФМ) являются такие, как – векторы, построенные на элементах алгебраических спектров соответственно собственных значенийи сингулярных чисел матрицы A.

Матричная функция от матрицы (МФМ) реализует отображение :Rⁿ^×ⁿRⁿ^×ⁿ. Исходное определение матричной функции от матрицы задается следующим образом.

Определение 6.3 (О6.3). Пусть– скалярный степенной ряд (многочлен) относительно скалярной переменной .

. (6.1)

Тогда скалярный ряд порождает матричную функциюот матрицыв виде матричного ряда, если в представлении (6.1) дляскалярную переменнуюзаменить на матрицутак, чтозапишется в форме

(6.2)

Поставим задачу построения перехода от исходного представления МФМ в форме (6.2) к ееминимальному представлению, то есть к представлению матричным многочленом минимальной степени. Начнем решение этой задачи с теоремы Гамильтона–Кэли.

Утверждение 6.1 (У6.1) (Теорема Гамильтона–Кэли).

Квадратная - матрицас характеристическим полиномом

, обнуляет свой характеристический полином так, что выполняется матричное соотношение

, (6.3)

где 0 – нулевая матрица. □

Доказательство справедливости сформулированного утверждения осуществим для случая матрицы простой структуры, характеризующейся алгебраическим спектром вещественных и некратных собственных значений так, что на нем может быть сконструирована диагональная матрица. Если теперь воспользоваться матричным соотношением подобия (2.30), то матрицуможно представить в форме, что в свою очередь для (6.3) позволяет записать

■

Теорема Гамильтона-Кэли позволяет ввести следующие определения.

Определение 6.4 (О6.4). Многочлен (степенной ряд) относительно скалярной переменнойназываетсяаннулирующим многочленом квадратной матрицы , если выполняется условие

(6.4)

Очевидно, аннулирующим многочленом матрицы в силу теоремы Гамильтона-Кэли является в первую очередь еехарактеристический полином. Ясно, что существует множество аннулирующих многочленов матрицы степени большей, чем. Но могут существовать аннулирующие многочлены степени .

Определение 6.5 (О6.5). Аннулирующий многочлен наименьшей степенисо старшим коэффициентом при, равным единице, называетсяминимальным многочленом матрицы .

Построим разложение многочлена (6.1), задающего матричную функциюот матрицы в форме (6.2), по модулю минимального многочленаматрицы, представив его выражением

, (6.5)

где многочлен имеет степеньменьше степениминимального многочленаматрицы. Выражение (6.5) позволяет дать следующее определение матричной функции от матрицы.

Определение 6.6 (О6.6). Пусть многочлен относительно скалярной переменнойдопускает представление в форме (6.5), тогда матричная функцияможет быть задана вминимальной форме

. (6.6)

Заметим, что основной проблемой при задании матричной функции от матрицы в форме (6.6) является вычисление многочлена .

Основной способ вычисления многочлена в силу (6.5) опирается на то, чтоявляется остатком от деленияна минимальный многочлен

. (6.7)

Если не является рядом или многочленом вида (6.1), а является произвольной аналитической функцией со значениями на алгебраическом спектре собственных значений матрицы , то формирование матричной функцииот матрицы, опирается на представлениев соответствии с интерполяционной схемой Лагранжа в виде мультипликативной структуры из двучленовили в соответствии с интерполяционной схемой Ньютона в виде ряда по степеням двучленов, число членов которых определяется минимальным многочленомДля реализации интерполяционной схемы Лагранжа, которая в случае размещения интерполяционных узлов на собственных значенияхматрицы, приобретает название интерполяционной схемы Лагранжа–Сильвестра, требуется знание значений. Для реализации интерполяционной схемы Ньютона требуется знание значений.

Если минимальный многочлен степенив силу его определения записать в форме

, (6.8)

где ,,

то можно построить представление для функции в форме

=, (6.9)

где –интерполяционный многочлен Лагранжа–Сильвестра или Ньютона, сформированный на алгебраическом спектре собственных значенийматрицы, характеризующийся степенью меньшей степениминимального многочлен, а потому удовлетворяющий условиям (6.5), (6.7).

Рассмотрим случай, когда нули минимального многочлена (6.8) являются простыми, т.е. при , минимальный многочлен и характеристический совпадают так, что выполняются равенстваи, тогда представлениев формеинтерполяционного многочлена Лагранжа–Сильвестра принимает вид

. (6.10)

Матричная функция от матрицы для случая некратных собственных значений матрицы принимает с использованием (6.10) вид

. (6.11)

Теперь допустим, что характеристический многочлен имеет кратные корни, номинимальный многочлен , являясь делителем, имеет только простые корни

В этом случае интерполяционный многочлен совпадает с точностью до замены числа членовнас представлением (6.10). Как следствие, матричная функцияот матрицыпринимает вид

. (6.12)

В заключение рассмотрим общий случай, когда минимальный многочлен матрицы имеет вид (6.8). Для случая кратных нулей минимального многочлена, то есть когда он имеет вид (6.8), представлениев формеинтерполяционного многочлена Лагранжа-Сильвестра, содержащего элементы интерполяционной схемы Ньютона, принимает вид

(6.13)

где для компактности записи использовано обозначение

Если ввести обозначение

, (6.14)

то выражение (6.13) для принимает вид

. (6.15)

Если воспользоваться представлением (6.15), то для МФМ можно записать

. (6.16)

Если матрица представляет собойжорданову клетку, порождаемую собственным значениемкратности, так что матрицапринимает вид

, (6.17)

то интерполяционный многочлен , так как минимальный многочлен матрицы(6.17) имеет вид, для функцииполностью строится по интерполяционной схеме Ньютона и определяется выражением

. (6.18)

В силу (6.18), (6.5), (6.7) матричная функция от матрицыпринимает вид

(6.19)

Рассмотрим теперь случай, когда матрица имеет вид, где–жорданова клетка, порождаемая собственным значением кратности, так что матрицапринимает вид

, (6.20)

тогда в силу (6.18) и (6.19) матричная функция от матрицы(6.20) принимает вид

. (6.21)

Из определения матричной функции от матрицы во всех формах следуют ее основные свойства:

Свойство 6.1 (СВ6.1). Матричная функция от матрицы f() сохраняет геометрический спектрсобственных векторовматрицы: , так что выполняется соотношение

, (6.22)

где – собственные значения матрицы f(), удовлетво-ряющие ее характеристическому уравнениюи вычисляемые как функцияна спектресобственных значений матрицыf().

Свойство 6.2 (СВ6.2). Матричная функция от матрицы f() сохраняет матричное отношение подобие в том смысле, что если матрицыиподобны, т.е., то

. (6.23)

Свойство 6.3 (СВ6.3). Матричная функция от матрицы f() сохраняет блочно-диагональную форму матрицыв том смысле, что, если, то

. (6.24)

Теперь распространим полученные результаты на задачи формирования способов аналитического представления и вычисления матричной экспоненты , параметризованной непрерывным временем, исходное задание которой в форме (6.1) порождено скалярной экспонентойили, записанной в форме бесконечного скалярного ряда

и принимает вид

. (6.25)

Следует заметить, что аналогичным образом может быть задана любая матричная функция от матрицы, для скалярного прототипа которой известен ряд ее представляющий.

В связи со сказанным и проведенными выше исследованиями, а также упомянутыми свойствами матричных функций от матриц, перечислим основные способы вычисления и построения аналитических представлений матричной экспоненты.

1. Численный способ, основанный на переходе от непрерывного времени к дискретному, выраженному в числе интервалов дискретности длительноститак, что, в результате чего матричная экспонентаполучает представление

, (6.26)

где матрица при правильном выборе интервала дискретностизадается конечным числомчленов степенного матричного представления

. (6.27)

При чем, если , то с помощью (6.7) ряд (6.27) может быть приведен кминимальной форме т.е. матричному ряду степени , а в случаек матричному ряду степениДля вычисления интервала дискретностиможно воспользоваться соотношением

. (6.28)

2. Способ диагонализации матрицы , именуемый иначе способом собственных значений. Способ применим к матрицампростой структуры так, что ее спектр собственных значений имеет вид, а потому оказывается справедливым матричное соотношение приведения подобия, где.

Тогда матричная экспонента принимает вид

, (6.29)

где

, (6.30)

то есть – матрица собственных векторов матрицы .

3. Способ, основанный на приведении к нормальной форме Жордана матрицы . Способ применим к матрицам , спектр собственных значений которых содержиткратных собственных значенийкратностикаждый. Для этого случая оказывается справедливым матричное соотношение приведения подобия, где

здесь ξ_i – собственный вектор матрицы , соответствующий собственному значению:; (*)⁺ – операция псевдообращения матрицы (*).

В результате для матричной экспоненты можно записать

, где матричная экспонента имеет вид

. (6.31)

4. Способ преобразования Лапласа заключается в вычислении обратного преобразования Лапласа от резолвенты в форме

. (6.32)

Способ поддерживается алгоритмом Фаддеева–Леверье разложения резольвенты без ее обращения на основе представления

где – матрицыи коэффициенты характеристического уравнения вычисляются с помощью рекуррентной процедуры алгоритма Фаддеева–Леверье:

. (6.33)

С использованием матриц для резолвентыможно записать в форме

=. (6.34)

Матричная экспонента (6.32) с использованием (6.34) получает представление

. (6.35)

Запишем характеристический многочлен в форме

тогда становится справедливым представление

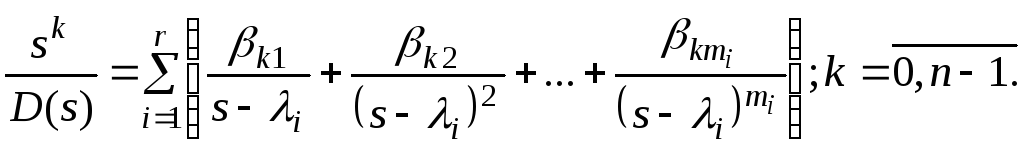(6.36)

Тогда

. (6.37)

Подставляя (6.37) в (6.35) окончательно получим

5. Способ Лагранжа–Сильвестра. Интерполяционный многочлен Лагранжа–Сильвестра в зависимости от свойств минимального многочлена определяется выражениями (6.11),(6.12),(6.16) которые после замены функциина,на,надают представлдение матричной экспоненты.

Решение вариантов задач

Задача 6.1. Найти матричную экспоненту способом, основанным на приведении к нормальной форме Жордана для матрицы;

Решение. Характеристический многочлен матрицыимеет видтак, что собственное значениехарактеризуется кратностьюВ свою очередь, характеристическая матрицаобладает нуль–пространствомразмерности, которому принадлежит один собственный вектор. В связи со сказанным нормальная форма Жордана матрицыпринимает канонический вид (6.17) и записывается в форме. Матрицаотношения подобия, так что, имеет представление

Тогда в силу свойства 6.2, а также представления (6.31) искомая матричная экспонентапринимает вид

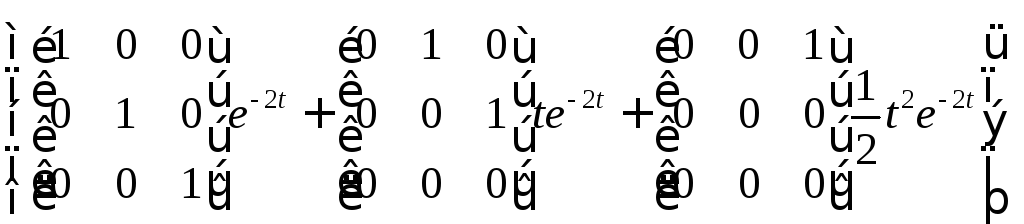
Раздел завершим рассмотрением кронекеровских (прямых) матричных структур, которые используются при решении матричных уравнений и описании процессов с перемножением переменных. Если компоненты кронекеровских матричных структур квадратные, то квадратной является и сама кронекеровская матричная структура, вычисление собственных значений которой осуществляется на основе свойств матричной функции от матрицы. Последнее обстоятельство стало определяющим для размещения приводимого материала в настоящем разделе.

Определение 6.7(О6.7). Кронекеровским произведением двух векторов и , , называется вектор , составленный из сепаратных произведенийих элементов так, что становится справедливым представление

, . (6.38)

Примечание 6.1(П6.1). Очевидно, кроме кронекеровского произведения двух векторов может быть построено также произведение этих же векторов, причем, в общем случае эти произведения оказываются не коммутативными так, что , хотя наборы компонентов у них одинаковые.

Определение 6.8(О6.8). Если размерности векторов и одинаковы, то на их кронекеровском произведении может быть построено согласованноесужение этого произведения , задаваемого представлением:

. (6.39)

Примечание 6.2(П6.2). Согласованное сужение кронекеровского векторного произведения может быть осуществлено с помощью оператора сужения с матрицейS вида

(6.40)

так, что становится справедливой запись:

. (6.41)

В качестве свойств кронекеровского произведения векторов рассмотрим правила дифференцирования кронекеровских векторных произведений по скалярному параметру, причем в основном сосредоточимся на случае, когда скалярным параметром является время.

Свойство 6.4(СВ6.4). Дифференцирование векторной кронекеровской структуры в виде их кронекеровского произведения осуществляется по правилам дифференцирования сложной функции, представленной в мультикативной форме так, что:

. (6.42)

Определение 6.9 (О6.9). Кронекеровским произведением прямоугольных матриц называется матрицаразмерности, составленная в силу соотношения

. (6.43)

Примечание 6.3(П6.3). Кронекеровское произведение произвольных прямоугольных матриц не обладает свойством коммутативности так, что

(6.44)

Определение 6.10 (О6.10). Кронекеровской суммой квадратных матриц и называется матрица , размерности, составленная в силу соотношения

, (6.45)

где - единичные матрицы, согласованные по размерности соответственно с матрицами А и В.

Примечание 6.4(П6.4). Для кронекеровской суммы квадратных матриц А и В, а в общем случае произвольного числа матриц, существует альтернативное название – преобразование Сильвестра матриц, что записывается в форме

. (6.46)

Для случая трех квадратных матриц А, В, С кронекеровская сумма или их преобразование Сильвестра будет записано в форме:

. (6.47)

Отметим, что как и кронекеровское произведение матриц кронекеровская сумма не коммутативна.

Кронекеровские матричные структуры, введенные выше, обладают следующими свойствами.

Свойство 6.5(СВ6.5). Алгебраический спектр собственных значений кронекеровского произведения квадратных матрицикакматричной функции от матриц обладает тем свойством, что его элементы образованы попарными произведениями собственных значений кронекеровски перемножаемых матриц:

.(6.48)

Свойство 6.6 (СВ6.6). Алгебраический спектр собственных значений кронекеровской суммы квадратных матрицикакматричной функции от матрицы обладает тем свойством, что его элементы образованы попарными суммами собственных значений кронекеровски суммируемых матриц:

. (6.49)

В (6.48) и (6.49) исобственные значения соответственно матриц А и В.

Сделаем следующее примечание к свойствам (СВ6.5) и (СВ6.6).

Примечание 6.5(П6.5). Алгебраические спектры собственных значений кронекеровских произведений ив силу (6.48) совпадают, аналогичным свойством в силу (6.49) обладают и спектры кронекеровских сумми.

Свойство 6.7(СВ6.7). Определитель кронекеровского произведения квадратных матриц удовлетворяет соотношению

, (6.50)

где и.

Свойство 6.8(СВ6.8). След кронекеровской суммы квадратных матриц удовлетворяет соотношению

, (6.51)

где и.

Свойство 6.9 (СВ6.9). Ранг кронекеровского произведения квадратных матриц удовлетворяет условию:

, (6.52)

где и.

Приведем без доказательств полезные свойства кронекеровских произведений произвольных матриц, в справедливости которых читатель может убедиться самостоятельно.

Свойство 6.10 (СВ6.10).

. (6.53)