fopi / Лабы по ФОИ - Изучение затухающих электромагнитных колебаний

Изучение затухающих электромагнитных колебаний

Приборы и принадлежности: электронный осциллограф, экспериментальная установка

Цель работы; изучение влияния емкости и активного сопротивления колебательного контура на параметры затухающих колебаний

Реальный колебательный контур состоит из конденсатора емкостью , Катушки индуктивности и обладает активным сопротивлением (рис. 22.1).

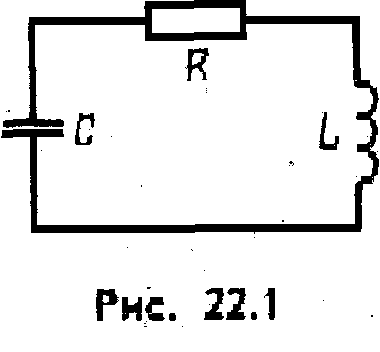
Если зарядить конденсатор, а затем предоставить ему возможность разряжаться через катушку и резистор, то в контуре возникнут затухающие электромагнитные колебания. При этом в катушке будет возникать э.д.с. самоиндукции

которая по закону Ома для замкнутой цепи равна сумме напряжений на конденсаторе и на резисторе .

Следовательно,

(22.1)

так как , то выражение (22.1) можно преобразовать:

Введя замену , можно записать:

(22.2)

Выражение-(22.2) является дифференциальным уравнением затухающих электромагнитных колебаний, .где -— коэффициент затухания, — круговая частота собственных колебаний системы.

Период собственных колебании системы определяется формулой Томсона:

Решение уравнения (22.2) зависит от знака разности ,

где — круговая частота затухающих колебаний. Если , то — действительное число и решением уравнения (22.2) будет выражение

(22.3)

где — максимальный заряд на обкладках конденсатора.

График функции (22.3) показан на рис. 22.2. Функция представляет собой закон изменения амплитуды. На рис. 22.2 график этой функции изображен пунктиром. Если , то колебаний нет и разряд конденсатора будет апериодическим.

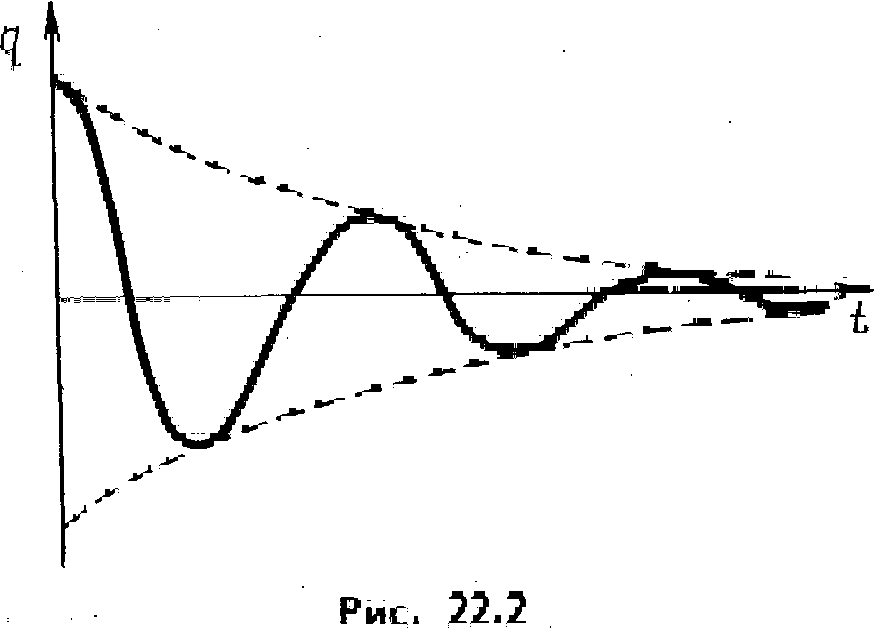
Из уравнений (22.3) можно получить законы изменения напряжения и силы тока в контуре:

(22.4)

(22.5)

Так как ,

где — период затухающих колебаний, то

,

,

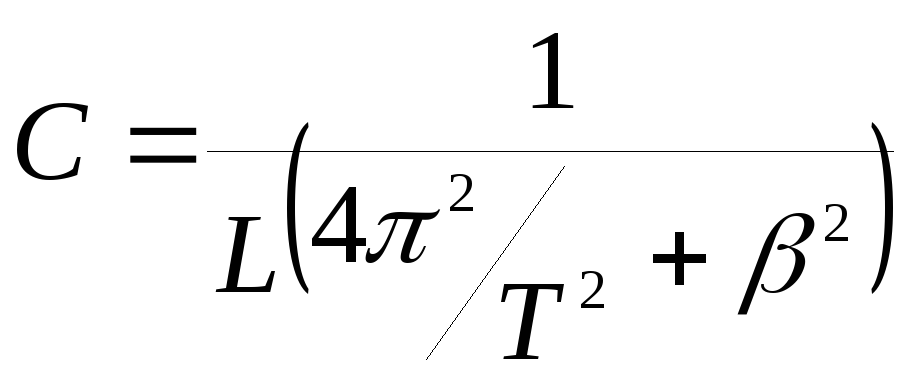(22.6)

Быстрота затухания колебаний определяется коэффициентом затухания : чем больше , тем быстрее уменьшается амплитуда колебаний. Степень затухания характеризуется также и логарифмическим декрементом затухания . Значение и связь его с коэффициентом затухания определяется выражениями

(22.7)

где - амплитуда сигнала в момент времени ,

и

. (22.8)

Подставив (22.7) и (22.8) в формулу (22.6), получим

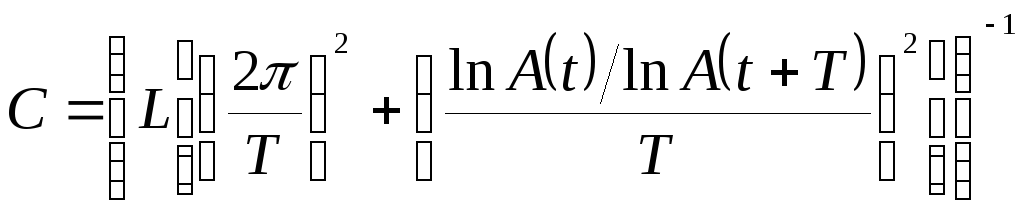(22.9)

Описание установки

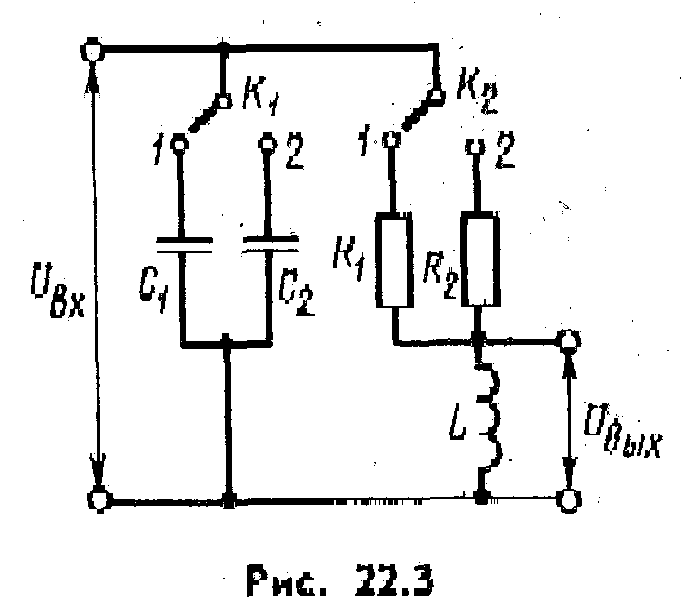
Схема установки изображена на рис. 22.3. Установка состоит из катушки индуктивности , конденсаторов и и резисторов и .

Переключателем можно включать в колебательный контур поочередно конденсаторы и , а переключателем — резисторы и . Таким образом, данная установка позволяет получить четыре колебательных контура с различными параметрами.

На конденсатор подастся пилообразное напряжение с генератора развертки электронного осциллографа. Выходной сигнал снимается с катушки индуктивности и подается на вход осциллографа. На экране осциллографа получается график затухающих электромагнитных колебаний.

Порядок выполнения работы

1. Установите переключатели и в положение 1, получите колебательный контур .

2. Включите осциллограф и добейтесь на экране устойчивой картины затухающих колебаний. Полученную кривую зарисуйте на миллиметровой бумаге.

3. Измерив расстояние и длительность развертки , определите период колебаний .

4. Измерив величину нескольких пар последовательных амплитуд и , определите, для каждой пары логарифмический декремент затухания , коэффициент затухания и емкость конденсатора [см. (22.7), (22.8), (22.9)] и вычислите и -

6. Результаты измерений и вычислений занесите в табл. 22.1.

6. Изменяя положение переключателей и , проведите аналогичные измерения и вычисления для колебательных контуров, и .

7. Вычислите и и найдите погрешности и измерения емкости конденсаторов с доверительной вероятностью .

Таблица 22.1

Контур	, см	, мкс/см	, с	, мм	, мм		, с-1	, Ф	, Ф

Вопросы и упражнения

1. Выведите дифференциальное уравнение затухающих электромагнитных колебаний и запишите его решение.

2. Что называется коэффициентом затухания и логарифмическим декрементом затуханий? Как они связаны?

3. Выведите формулу для определения емкости конденсатора в данной работе.