itmo373

Передний фокальный отрезок SF – это расстояние от вершины передней поверхности до переднего фокуса.

Если f ′ > 0 , то система называется собирающей или положительной.

Если f ′ < 0, то система рассеивающая или отрицательная.

Переднее и заднее фокусные расстояния не являются абсолютно независимыми, они связаны между собой соотношением:

Выражение (5.2.5) можно переписать в виде:

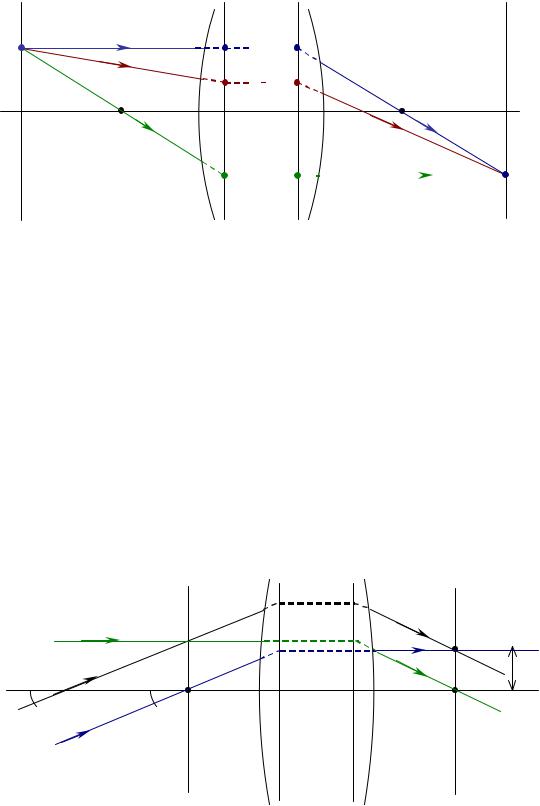
бы два вспомогательных луча, на пересечении которых и будет находиться точка A′ (рис.5.2.5). Вспомогательный луч 1 можно провести через точку A параллельно оптической оси. Тогда в пространстве изображений луч 1′ пройдет через задний фокус оптической системы. Вспомогательный луч 2 можно провести через точку A и передний фокус оптической системы. Тогда в пространстве изображений луч 2′ пойдет параллельно оптической оси. На пересечении лучей 1′ и 2′ будет находиться изображение точки A . Теперь в точке A′ пересекаются все лучи (1 - 2 - 3), выходящие из точки A.

70

H H′

Рис.5.2.5. Построение изображения точки.

Построим теперь ход луча r (рис.5.2.6).

1 способ. Можно построить вспомогательный луч, параллельный данному и проходящий через передний фокус (луч 1). В пространстве изображений луч 1′ будет идти параллельно оптической оси. Так как лучи r и 1 параллельны в плоскости предметов, то в пространстве изображений они должны пересекаться в задней фокальной плоскости. Следовательно, луч r′ пройдет через точку пересечения луча 1′ и задней фокальной плоскости.

2 способ. Можно построить вспомогательный луч, идущий параллельно оптической оси и проходящий через точку пересечения луча r и передней фокальной плоскости (луч 2 ). Соответствующий ему луч в пространстве изображений (луч 2′) будет проходить через задний фокус. Так как лучи r и 2 пересекаются в передней фокальной плоскости, в пространстве изображений они должны быть параллельными. Следовательно, луч r′ пойдет параллельно лучу 2′.

5.3. Основные соотношения параксиальной оптики

Основные соотношения параксиальной оптики связывают между собой фокусные расстояния, положение и размеры предмета и изображения, угловое, линейное и продольное увеличения.

71

5.3.1. Вывод зависимости между положением и размером предмета и изображения

Рис.5.3.1. Схема для вывода основных соотношений параксиальной оптики.

Для вывода зависимости между положением и размером предмета и

Выразим z и z′ через фокусные расстояния и передний (−a) и задний (a′) отрезки:

z′ = a′− f ′

72

z = a − f

Тогда выражение (5.3.3) можно записать в виде:

(a − f ) (a′− f ′)= f f ′

После преобразований получим выражение, связывающее фокусные расстояния и передний и задний отрезки (формула отрезков или формула Гаусса):

5.3.2. Угловое увеличение и узловые точки

Теперь рассмотрим угловое увеличение, воспользовавшись снова рис.5.3.1. Из OK1H , видно, что:

tg(−α)= −ya =α , отсюда −α = −ya

Аналогично можно вывести выражение:

α′ = ay′

Теперь можно выразить угловое увеличение через соответствующие отрезки (а и а’, z и z’):

в пространстве предметов (изображений) угловое увеличение равно единице. Такие точки называются узловыми точками.

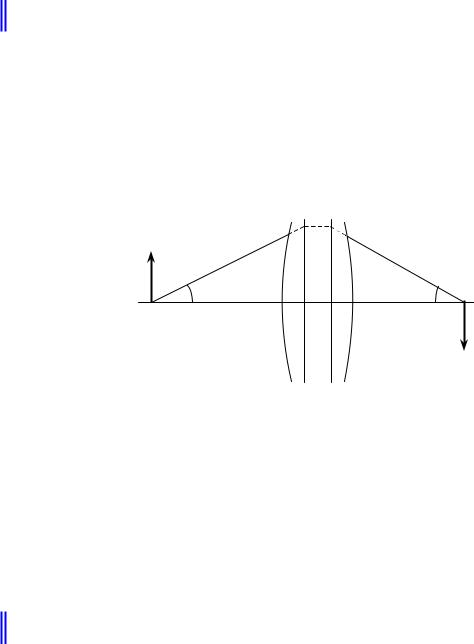
Чтобы найти узловые точки N и N ′, от переднего фокуса откладывается заднее фокусное расстояние, а от заднего фокуса откладывается переднее фокусное расстояние (рис.5.3.2). Отрезки NN ′ и HH ′ равны. Если − f ′= f ( n = n′), то узловые точки совпадают с главными точками.

Следствием выражений (5.3.2) и (5.3.7) является следующее соотношение:

73

Рассмотрим рис.5.3.3. Длину отрезков l и l′ можно выразить следующим образом:

l = z1 − z l′ = z′− z1′

По определению продольного увеличения (5.2.4):

Q = l′ = z′− z1′ l z1 − z

После преобразований, с учетом выражений (5.3.1) и (5.3.2), получим:

То есть продольное увеличение равно квадрату линейного увеличения, а угловое обратно пропорционально ему.

5.3.5. Диоптрийное исчисление

Диоптрийное исчисление – это измерение продольных отрезков в обратных единицах (диоптриях):

D= a −1 , [дптр]

n

где an – приведенная длина.

Одна диоптрия соответствует приведенному отрезку в 1м. Если отрезок измеряется в мм, то обратный отрезок измеряется в килодиоптриях.

75

Используя формулу отрезков (5.3.5) и выражение (5.2.5) можно получить важное соотношение для приведенных отрезков в пространстве предметов и изображений и оптической силы, измеряемых в диоптриях:

есть оптическая система увеличивает приведенный отрезок в пространстве изображений (в дптр) на величину оптической силы.

5.3.6. Инвариант Лагранжа-Гельмгольца

Инвариант Лагранжа-Гельмгольца связывает линейный размер предмета и угловой размер пучка лучей (рис.5.3.4). Эта величина инвариантна, то есть неизменна в любом пространстве.

Рис.5.3.4. Величины, которые связывает инвариант Лагранжа-Гельмгольца.

Для вывода этого инварианта воспользуемся выражением (5.3.8), связывающим угловое и линейное увеличения. Тогда воспользовавшись выражениями (5.2.1) и (5.2.3), определяющими линейное и угловое увеличения, получим следующее соотношение:

Выражение (5.3.15) можно преобразовать, и тогда получим инвариант Лагранжа-Гельмгольца:

Инвариант Лагранжа-Гельмгольца характеризует информационную емкость оптической системы, то есть величину пространства, которое может быть отображено оптической системой. Этот инвариант математически выражает закон сохранения информации в геометрической оптике.

76

Вместо угла α часто используют направляющий косинус Y оптического лучевого вектора:

Y = n cos βy = −n sinα = −n α

где βy – угол между лучом и осью y , n α – приведенный угол.

Для лучей в меридиональной плоскости направляющий косинус X = 0 , таким образом, в параксиальной оптике луч может быть однозначно определен через линейную координату y и угловую координату Y = −n α :

77

Аналогично, луч в пространстве изображений описывается линейной координатой y′ и угловой координатой Y ′ = −n′ α′:

6.1.2. Преобразование координат оптических лучей

Действие оптической системы заключается в преобразовании координат лучей:

Разложим выходные координаты луча в ряд: y′ = a0 + a1 y + a2Y + a3 y2 + a4 yY + a5Y 2 +...

Y ′ = b0 + b1 y + b2Y + b3 y2 + b4 yY + b5Y 2 +...

Если оптическая система является центрированной, то a0 = b0 = 0 . Все члены ряда, начиная с a3 и b3 , можно отбросить, так как они стремятся к нулю

на порядок быстрее, чем предыдущие. Таким образом, для идеальной оптической системы:

y′= Ay + BY

(6.1.3)

Y ′= Cy + DY

6.2.Матрица преобразования лучей

6.2.1.Общий вид матрицы преобразования (ABCD-матрица)

Выражение (6.1.3) для преобразования линейной и угловой координат луча, рассмотренные в параграфе 6.1, можно записать в матричной форме, тогда преобразование координат луча оптической системой можно представить в виде умножения некоторой матрицы вектора на вектор входных координат луча:

Все свойства идеальной оптической системы полностью описываются

матрицей преобразования лучей G , называемой также гауссовой матрицей

или ABCD-матрицей:

Выражение (6.2.1) можно также записать в виде:

78

где b – вектор-столбец входных координат, b′ – вектор-столбец выходных координат, G – матрица, описывающая оптическую систему.

6.2.2. Геометрический смысл элементов матрицы преобразования

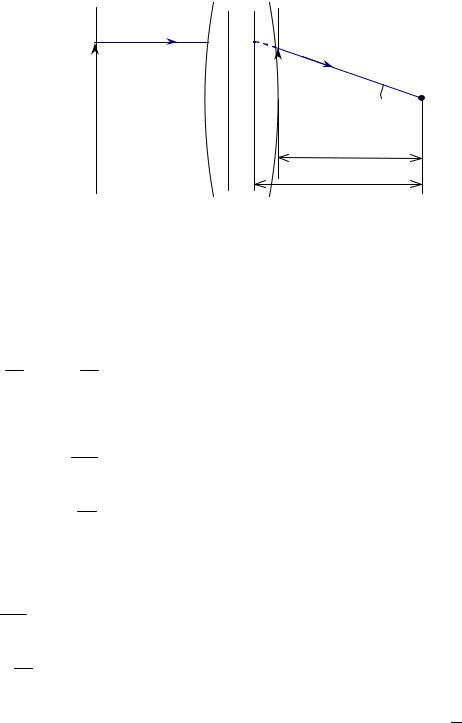
Рассмотрим луч с координатами y =1, Y = 0 (рис.6.2.1).

SF′ ′

f ′

Рис.6.2.1.Схема для нахождения элементов A и C матрицы преобразования.

Подставив в выражение (6.1.3) значения y и Y ′, получим:

y′= Ay + BY = A

(6.2.4)

Y ′= Cy + DY = C

Из рис.6.2.1 видно, что: f ′ = αy′, SF′ ′ = αy′′

Отсюда с учетом того, что y =1, можно получить выражения для y′ и Y ′:

y′= SF′ ′ α′= SfF′′′

(6.2.5)

Y ′= −n′α′ = − nf ′′

Таким образом, подставив выражения (6.2.5) в (6.2.4), мы получим два элемента матрицы преобразования:

A = SfF′′′

(6.2.6)

C = − nf ′′ = −Φ

Теперь рассмотрим луч с входной координатой Y =1 (α = − n1 ) и выходной координатой Y ′= 0 (α′ = 0 ) (рис.6.2.2).

79