itmo373

z

dЩ dS

θ dθ

dϕ

x

Рис. 2.4.1. Телесный угол в полярных координатах.

2.4.1. Сферический ламбертовский излучатель

Для сферического ламбертовского излучателя сила света постоянна во всех направлениях: I (ϕ,θ) = I0 = const .

Поток в телесном угле Ω0 определяется из выражения (2.4.2):

z

Щ0

2у

у

y

x

Рис.2.4.2. Телесный угол, получаемый вращением плоского угла.

Найдем телесный угол Ω0 , определяемый плоским углом 2σ (рис.2.4.2):

Таким образом, телесный угол, который получается вращением плоского угла можно выразить следующим образом:

30

Тогда полный поток от сферического ламбертовского излучателя в телесном угле Ω0 определяется выражением:

Таким образом, полный поток от плоского ламбертовского излучателя в телесном угле Ω0 , определяемым плоским углом 2σ , можно выразить

следующим образом:

При малых углах выражения (2.4.5) и (2.4.7) для потока излучения сферического и плоского источников дают одинаковый результат.

2.5. Яркость рассеивающей поверхности

Рассмотрим ламбертовское рассеяние: рассеяние света плоской поверхностью происходит по всем направлениям, и не зависит от телесного угла, в пределах которого падает световой поток. Световой поток выходит после такого рассеивателя равномерно распределенным в пределах телесного угла 2π . Примером может служить белая бумага или молочное стекло. Яркость такой поверхности постоянна по всем направлениям и не зависит от направления падающего света, то есть полностью подчиняется закону Ламберта. Кривая распределения силы света таких поверхностей имеет форму окружности (рис.2.5.1).

Рис.2.5.1. Ламбертовское рассеяние.

Часть падающего потока Φ поглощается поверхностью, и рассеивается поток Φ′:

31

Отсюда яркость идеального рассеивателя:

2.6.1. Освещенность, создаваемая точечным источником

Рассмотрим точечный источник.

Точечный источник – это источник, размерами которого можно пренебречь по сравнению с расстоянием до него, и который излучает поток, равномерный по всем направлениям.

Освещенность площадки dS , создаваемая точечным источником:

E = ddSΦ = IddSΩ = I cosr2 θ

32

N

r θ

dΩ dS

I

Рис.2.6.1. Освещенность, создаваемая точечным источником.

Закон обратных квадратов:

Освещенность, создаваемая точечным источником обратно пропорциональна расстоянию от источника до поверхности и прямо пропорционально косинусу угла, между направлением светового потока и нормалью к освещаемой поверхности:

где I – сила света источника в направлении освещаемой точки. Практические измерения показывают, что для соблюдения закона

обратных квадратов отношение размера источника к расстоянию до него должно быть меньше 0.1.

2.6.2. Освещенность от протяженного ламбертовского источника

dS

x

Рис.2.6.2 Освещенность от протяженного ламбертовского источника.

Для протяженного источника можно разбить поверхность источника на элементарные площадки dS (рис.2.6.2) и определить освещенность, создаваемой каждой из них по закону обратных квадратов (2.6.1):

33

Проинтегрируем теперь элементарную освещенность по всей площади источника:

Так как у ламбертовского источника яркость постоянна по всем направлениям, ее можно вынести за интеграл:

направляющие косинусы.

Можно показать, что выражения (2.6.4) и (2.6.5) эквивалентны, если учесть, что dqx = −sinαxdαx , dqy = −sinαydαy , dαxdαy = dΩ, а углы β и θ являются дополнительными к αx , αy .

34

3. Прохождение света через границу раздела двух сред

3.1. Отражение и преломление света на границе раздела двух сред

Рассмотрим падение плоской волны на границу, разделяющую две прозрачные однородные диэлектрические среды с показателями преломления n и n′. Будем считать, что граница представляет собой плоскость (так как в пределах бесконечно малой области любую поверхность можно считать плоской). Будем также считать, что сама граница раздела свет не поглощает.

После прохождения границы раздела двух сред падающая плоская волна (луч i ) разделяется на две волны: проходящую во вторую среду (луч t ) и отраженную (луч r ) (рис.3.1.1).

z

Рис.3.1.1. Преломление и отражение света на границе двух сред.

На рис.3.1.1 N – вектор нормали к поверхности в точке падения единичной длины (N =1). Поместим начало координат в точку падения. Определим

следующие величины:

Угол падения ε – это угол между лучом i , падающим на преломляющую или отражающую поверхность, и нормалью N к поверхности в точке падения.

Угол преломления ε′ – это угол между преломленным лучом t и нормалью N к поверхности в точке преломления.

Угол отражения ε – это угол между отраженным лучом r и нормалью N к поверхности в точке отражения.

3.1.1. Закон преломления

После прохождения светом границы раздела двух сред необходимо определить направление распространения преломленной волны t и отраженной волны r , и распределение энергии между отраженной и преломленной волной.

В соответствии с уравнением плоской волны (1.4.9) запишем выражения для комплексных амплитуд падающей, отраженной и преломленной волн:

уравнение падающей плоской волны

35

преломленной волн, k0 – волновое число, r – радиус-вектор произвольной точки.

Здесь мы используем соотношения скалярной теории, поскольку закон преломления одинаков для векторных и скалярных волн.

Из уравнений падающей и преломленной плоской волны следует, что на границе раздела двух сред у падающей и преломленной волн амплитуды могут быть различны, но должны совпадать значения эйконалов (этого требует условие физической реализуемости, так как иначе волна будет иметь разрыв на границе раздела):

Равенство (3.1.4) соблюдается на границе раздела, то есть для всех r , перпендикулярных вектору нормали. Таким образом, выражение (3.1.4) можно записать в виде:

(qt ,r)−(qi ,r)= 0 при (r, N)= 0

или:

((qt − qi ),r)= 0 при (r, N)= 0

То есть (qt −qi ) r , если N r . Выполнение этих условий возможно тогда и только тогда, когда (qt −qi )|| N . Таким образом, можно вывести

Закон преломления (refraction law):

качественная часть закона:

падающий луч, преломленный луч и нормаль к поверхности раздела двух сред в точке падения лежат в одной плоскости.

количественная часть закона:

36

произведение показателя преломления на синус угла между лучом и нормалью сохраняет свое значение при переходе в следующую среду:

Величина Γ имеет большое значение в математическом аппарате расчета лучей (ray tracing) на компьютере.

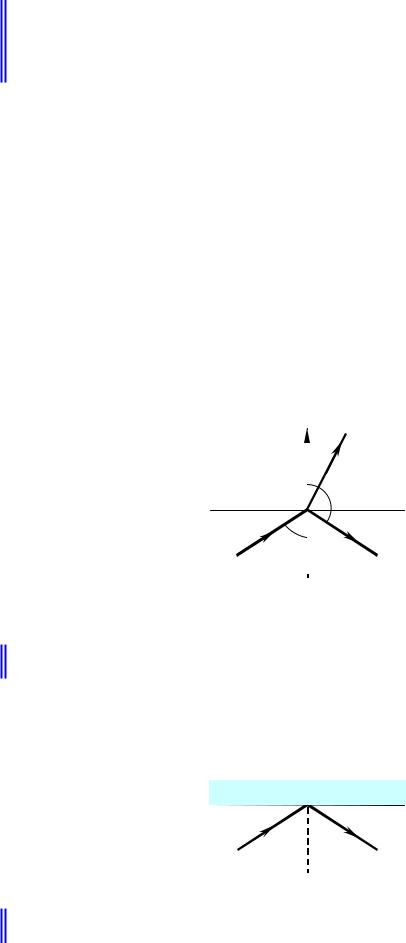
3.1.2. Закон отражения

Закон отражения можно вывести в векторной форме аналогично закону преломления, подставив вместо оптического вектора преломленного луча qt

оптический вектор отраженного луча qi (рис.3.1.2).

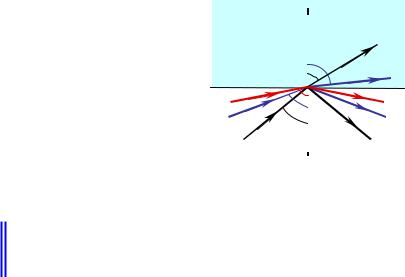
Закон отражения можно представить как частный случай закона преломления при n′ = −n (рис.3.1.3). Следует отметить, что в отрицательном значении показателя преломления нет никакого физического смысла, это просто прием для удобства расчета лучей в геометрической оптике.

Рис.3.1.3. Отражение света на границе двух сред.

37

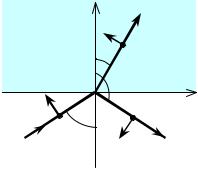
3.1.3. Полное внутреннее отражение

Если угол падения ε невелик, то часть поля отражается, а часть преломляется. Однако, при переходе из более плотной среды в менее плотную (n > n′), при некотором угле падения синус угла преломления по закону преломления должен быть больше единицы, что невозможно. Поэтому в таком случае преломления не происходит, а происходит полное внутреннее отражение (ПВО, entire inner reflection) (рис.3.1.4):

2

ПВО – это явление отражения электромагнитных волн от границы раздела двух прозрачных сред при условии, что волна падает из среды с большим́ показателем преломления и при условии, что угол падения превосходит некоторый критический угол. Коэффициент отражения при ПВО не зависит от длины волны. ПВО широко используется в оптической технике благодаря тому, что при ПВО падающая волна отражается полностью, то есть потерь энергии нет.

Нарушение полного внутреннего отражения (НПВО) заключается в том, что коэффициент отражения света от границы раздела сред становится меньше единицы вследствие поглощения света в приграничном слое отражающей среды. Степень ослабления отражённой волны зависит от поляризации падающей волны и пропорциональна показателю поглощения отражающей среды, а спектр НПВО подобен спектру поглощения этой среды. НПВО, несущественное для геометрической оптики, послужило основой для развития спектроскопии НПВО, имеющей ряд преимуществ перед традиционными методами исследования спектров отражения и поглощения. Особенно эффективен метод НПВО для исследований поверхностных оптических свойств объектов, а также для сильно поглощающих сред.

38

3.2. Формулы Френеля. Соотношение между амплитудами падающих, преломленных и отраженных волн

При выводе законов преломления и отражения (параграф 3.1) не принимались во внимание энергетические соотношения между падающим, преломленным и отраженным лучами. Для учета этих соотношений необходимо использование векторного описания падающего поля.

3.2.1. Формулы Френеля

Рассмотрим, какое количество света преломляется, а какое отражается, в зависимости от угла падения и показателей преломления сред. Эта задача была решена в первой половине XIX века Френелем (Fresnel).

Рассмотрим границу раздела двух сред с показателями преломления n и

n′. Разложим электрический вектор падающей плоской волны E(i ) на две составляющих: одна лежит в плоскости падения ( A|| ), другая перпендикулярна

плоскости падения (и плоскости рисунка) ( A ) (рис.3.2.1).

Рис.3.2.1. Отражение и преломление плоской волны. Формулы Френеля.

Тогда компоненты электрического вектора поля падающей плоской волны запишутся в виде:

Ez(i) = A|| sinε

Поскольку вектор H перпендикулярен вектору E , то его компоненты можно выразить следующим образом:

H x(i) = −A n cosε

Hz(i) = A nsinε

Аналогично можно разложить комплексную амплитуду отраженной волны R и преломленной волны T на параллельную и перпендикулярную составляющие.

Тогда поле прошедшей волны:

39