
itmo373
.pdfu = a e2πi ν b |
|
|
|
|
(9.1.6) |
||
Тогда интенсивность гармонической решетки в комплексной форме: |
|||||||
I (xθ )= u e |
2πi ν xθ |
|
|
|
|
(9.1.7) |
|
|
|
|
|
|
|||
Величину xθ можно |
выразить |
как |
xθ = x cosθ + y sinθ , тогда |
||||
интенсивность гармонической решетки будет зависеть от двух координат (x, y): |
|||||||
I (xθ )= u e |
2πi(x ν cosθ + y ν sinθ ) |
= u e |
2πi(ν x x +ν y y ) |
~ |
(9.1.8) |
||
|
|
|
|
= I (x, y) |
|||
где νx – частота в направлении x , νy |
– частота в направлении y . |
|
|||||
Любой объект, как было сказано выше, можно разложить на элементарные гармонические объекты, тогда изображение – это совокупность изображений элементарных объектов. Эти изображения для реальных оптических систем всегда имеют искажения, обусловленные выполнением закона сохранения энергии. Следует отметить, что идеальным оптическим системам свойственно нарушение закона сохранения энергии, так как они для сохранения неизменной структуры предмета должны передавать бесконечно большую энергию.
Изображение гармонического объекта можно описать, если в выражение (9.1.3) подставить в качестве распределения интенсивности на предмете функцию I~(x, y) (9.1.8):
~′ ′ ′ |
)= |
+∞ +∞~ |
(x, y) h(x |
′ |
−Vx, y |
′ |
−Vy) dxdy |
(9.1.9) |
I (x , y |
∫ ∫I |
|
|
−∞ −∞
Если выразить координаты предмета и изображения в едином масштабе, то V =1, следовательно:
~ |
|
|
|
+∞ +∞ |
|
2πi(ν x x +ν y y ) |
|
|
|
|
|
|
|
|
|
|
′ |
|
′ |
)= ∫ |
∫u e |
h(x |
′ |
|
|
|
′ |
− y) dxdy |
|
||||
′ |
|
|
− x, |
y |
|
|||||||||||
I (x , y |
|
|
|
|
|
|||||||||||
|
|
|
|
−∞ −∞ |
|
|
x′− x = v , |
dx = −dv |
, x = x′−v |
|
||||||
После замены переменных |
получим: |
|||||||||||||||
|
|
|
|
|
|
|
|
y′− y = w |
dy = −dw |
y = y′− w |
|
|||||
~ |
|
|
|
+∞+∞ |
|
2πi(νx (x′−v)+ν y (y′−w)) |
h(ν, w) dνdw |
|
|
|||||||
I ′(x′, y′) |
= ∫ ∫u e |
|
|
|
|
|||||||||||
|
|
|
|
−∞−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
или, после переобозначения ν = x , w = y : |
|
|
||||||||||||||
~ |
|
|
|
+∞ +∞ |
|
2πi(ν x (x′−x )+ν y (y′− y )) |
|
|
|
|
|
|
||||
′ |
′ |
)= ∫ |
∫u e |
h(x, y) dxdy = |
|
|||||||||||
′ |
|
|
|
|
|
|||||||||||
I (x , y |
|
|
|
|
|
|
||||||||||
|
|
|
|
−∞ −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
+∞ +∞ |
|
|
(ν x x′+ν y y′) e−2πi(ν x x +ν y y ) h(x, y) dxdy = |
|
|||||||||||
= |
∫ |
∫u e2πi |
(9.1.10) |
|||||||||||||
|
−∞ −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
=u e2πi(ν x x′+ν y y′) +∫∞ +∫∞h(x, y) e−2πi(ν x x +ν y y ) dxdy =
=u e2πi(ν x x′+ν y y′) −∞D(ν−∞x ,νy )
130

Двойной интеграл в выражении (9.1.10) – это некоторая функция D(νx ,νy ),
зависящая от пространственных частот.
Обозначим u′= u D(νx ,ν y ), и запишем распределение интенсивности на изображении гармонического объекта в следующем виде:
~ |
|
)= u |
′ |
|
2πi(ν x x′+ν y y′) |
|
′ ′ ′ |
e |
|
(9.1.11) |
|||
I |
(x , y |
|
|
|||
Как показывают соотношения (9.1.8) и (9.1.11), изображение от предмета отличается только комплексной амплитудой, то есть изображение гармонической решетки любой оптической системы есть гармоническая решетка с той же частотой. Поэтому гармоническую решетку удобно использовать для исследования и оценки передачи структуры изображения. Изменение комплексной амплитуды гармонической решетки – это и есть действие оптической системы.
9.1.4. Оптическая передаточная функция (ОПФ)
Оптическая передаточная функция (optical |
transfer function, OTF) |
D(νx ,ν y ) характеризует передачу структуры |
предмета оптической |
системой как функция пространственных частот: |
|
u′= u D(νx ,ν y ) |
(9.1.12) |
ОПФ связана с ФРТ интегральным преобразованием – преобразованием Фурье:
+∞ +∞ |
|
|
D(νx ,νy )= ∫ ∫h(x, y) e−2πi(ν x x+ν y y ) dxdy |
(9.1.13) |
|
−∞ −∞ |
|
|
или |
|
|
ОПФ = F[ФРТ] |
|
|
или |
|
|
F |
|
|
ФРТ ↔ОПФ |
|
|
где F – обозначение Фурье-преобразования: |
|
|
+∞ +∞ |
−2πi(ν x x +ν y y ) dxdy |
|
F[f (x, y)]= ∫ ∫ f (x, y) e |
(9.1.14) |
|
−∞ −∞
ФРТ показывает, как оптическая система изображает точку, а ОПФ показывает, как оптическая система изображает гармоническую решетку, то есть как меняется комплексная амплитуда решетки в зависимости от частоты.
Оптическая передаточная функция – это комплексная функция:
|
|
|
D(νx ,ν y )=T (νx ,ν y ) eiϕ(ν x ,ν y ) |
|
|
|
|
|
|
(9.1.15) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
Модуль |
ОПФ T (νx ,ν y )= |
|
D(νx ,ν y ) |
|
|
называется модуляционной |
||
|
|
|
|||||||||
|
|
|
|
|
|||||||
передаточной |
функцией |
(МПФ) |
или |
частотно-контрастной |
|||||||
131
характеристикой (ЧКХ). Аргумент (фаза) ОПФ ϕ(νx ,ν y )= arg[D(νx ,ν y )]
называется фазовой передаточной функцией (ФПФ) или частотно-фазовой характеристикой (ЧФК).
Частотно-контрастная характеристика показывает передачу вещественной амплитуды гармонического объекта:
ЧКХ = |
a′ |
|
|
|
|
|
|
|
|
|
(9.1.16) |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
где a – амплитуда на предмете, a′ |
– амплитуда на изображении. |
|||||||||||
Амплитуда изображения гармонического объекта тесно связана с |
||||||||||||
контрастом. |
Контраст для |
периодических (гармонических) |
изображений |
|||||||||
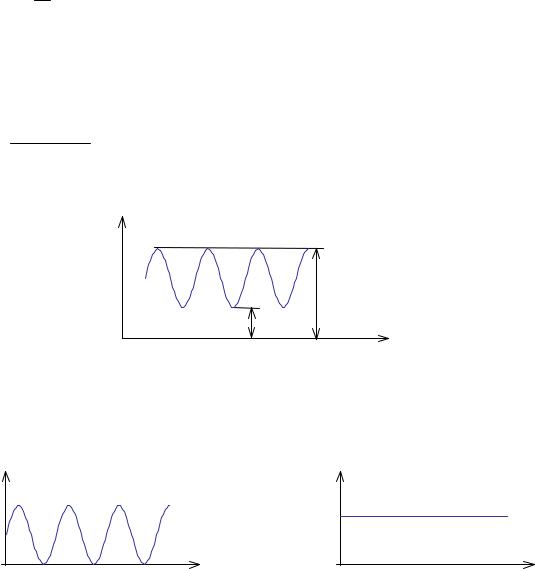
(рис.9.1.4) определяется выражением: |
|
|
|
|
|
|
||||||
|
′ |
′ |
|
|
|
|
|
|
|
|
|
|
k′ = |
Imax − Imin |
, |
|
|
|
|
|
|
|
|
(9.1.17) |
|
′ |
′ |
|
|
|
|
|
|
|
|
|||
|
Imax + Imin |
|
|
|
|
|
|
|
|
|
|
|
0 ≤ k′ ≤1. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
I ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
Imax |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
x′ |
|
|
|
|
|
|
|
|
|
|
|
Imin |
|
|
|
|
|
Рис.9.1.4. Контраст гармонического объекта. |
|
|||||||||
Абсолютный |
контраст |
k |
′ |
=1 |
получается, |
когда |
′ |
(рис.9.1.5.а). |
||||
|
Imin = 0 |
|||||||||||
Контраст |
в |
изображении нулевой |
k |
′ |
= 0 , когда |
′ |
′ |
этом случае |
||||
|
Imin = Imax , в |
|||||||||||
изображение практически отсутствует (рис.9.1.5.б).
I ′ |
I ′ |
x′ |
x′ |
а) абсолютный контраст |
б) нулевой контраст |
Рис.9.1.5. Абсолютный и нулевой контраст гармонического объекта.
Чем больше контраст, тем лучше различаются мелкие детали изображения. Изображение нельзя зарегистрировать или увидеть в случае, если:
k′<δk′ |
(9.1.18) |
где δk′ – порог контраста, зависящий от приемника изображения (например, для глаза δk′≈ 0.05 ).
132
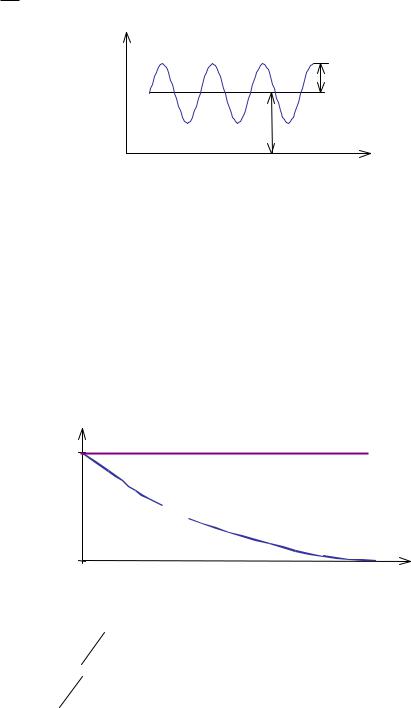
Контраст для изображения гармонического объекта может быть выражен через постоянную a0′ и переменную a′ составляющие изображения
гармонического объекта (рис.9.1.6):
k′ = a′ (9.1.19) a0′
I ′
a′
a′0 x′
Рис.9.1.6. Постоянная и переменная составляющие изображения гармонического объекта.
|
|
Если |
a0′ = a0 , то ЧКХ, как следует из выражения |
(9.1.16) будет |
||
определяться следующим соотношением: |
|
|||||
|
|
ЧКХ = |
|
k ′ |
|
(9.1.20) |
|
k |
|||||
|
|
|
|
|
||
|
|
где k′ – контраст изображения, k – контраст предмета. |
|
|||
|
|
Частотно-контрастная характеристика показывает зависимость контраста |
||||
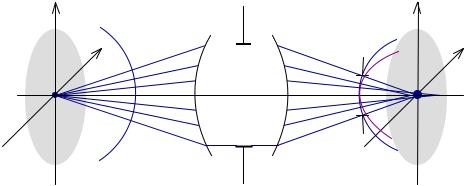
изображения гармонической решетки от частоты решетки, если считать, что на предмете контраст единичный (рис.9.1.7). Для идеальной оптической системы ЧКХ – прямая, параллельная оси.
k′
1
идеальная о.с.
 реальная о.с.
реальная о.с.
ν x
0
Рис.9.1.9. Частотно-контрастная характеристика.
Для ближнего типа предмета или изображения пространственная частота ν
измеряется в лин |
мм |
. Для дальнего типа пространственная частота |
|
|
измеряется в лин рад .
Итак, передача структуры изображения описывается ФРТ или ОПФ, которые связаны через взаимно однозначные преобразования Фурье. Наглядно отобразить двумерную функцию ОПФ можно в виде:
•графиков сечений T (νx ) или T (ν y ),
•изометрического изображения “поверхности” T (νx ,ν y ),
•карты уровней T (νx ,νy ).
133
9.2. Схема формирования оптического изображения
Существует два оптических явления, которые влияют на структуру и качество изображения в оптической системе - дифракция и аберрации. Эти явления действуют совместно. Если аберрации малы и преобладает дифракция, то такие системы называются дифракционно-ограниченными. Если аберрации велики, и дифракция становится незаметной на фоне аберраций, то такие системы называются геометрически-ограниченными (формирование изображения вполне корректно описывается с позиций геометрической оптики, без привлечения теории дифракции).
плоскость |
y |
|
|
y′ |
|
|
x |
|
вых. зр. |
x′ |
|
|
|
предметов |
|
|
|
|||
|
|
|
||||
U (x, y) |
|
|
|
U |
(x , y |
) |
|
|
|
|
|
′ ′ ′ |
|
A0 |
|
′ |
A0′ |
|
|
плоскость |
|
|
|
Sw |
|
S |
|
S′p |
изображений |
w |
|
||
|
А.Д. |
|
Рис.9.2.1. Схема формирования оптического изображения.
Рассмотрим формирование изображения некоторой точки (рис.9.2.1). Гомоцентрический пучок лучей выходит из точки A0 , и после идеальной
оптической системы сходится в точке A0′ . Наряду с пучками лучей можно также рассматривать сферические волновые фронты Sw и Sw′ . Действие реальной оптической системы сводится к следующим факторам:
•преобразование расходящегося пучка лучей (волнового фронта) в сходящийся,
•ограничение размеров проходящего пучка лучей или волнового фронта,
•ослабление интенсивности (энергии) проходящего поля,
•нарушение гомоцентричности пучка или сферичности волнового
фронта, то есть изменение фазы проходящего поля.
Рассмотрим поле U ′(Px′, Py′) на выходной сфере (в области выходного
зрачка). Волновой фронт близок к выходной сфере, но отличается от нее на величину волновой аберрации. Поле на волновом фронте U в′.ф. (Px′, Py′).
Оптический путь из центра предмета до волнового фронта для всех лучей одинаковый, так как волновой фронт – поверхность равного эйконала. Поскольку для формирования изображения важна разность фаз между выходной сферой и волновым фронтом, а не сама фаза, то можно принять, что фаза волнового фронта равна нулю ϕ = 0 . При отсутствии аберраций амплитуда поля единичная, следовательно поле на волновом фронте U в′.ф. (Px′, Py′)=1. Набег
фазы от выходной сферы до волнового фронта:
134

ϕ = e |
2πi |
l′ n′ |
(9.2.1) |
|
λ |
||
|
|
где l′ – расстояние между волновым фронтом и выходной сферы вдоль луча.
Поле на выходной сфере математически можно представить в виде:
U ′(Px′, Py′)= |
|
2πiW (Px′ ,Py′ ) |
, внутри зрачка = f (Px′, P′) |
|
||
e |
|
|
|
(9.2.2) |
||
|
|
|
|
|
|
|
|
0, вне зрачка |
|
||||
где W (Px′, Py′)= |
|
l′ n′ |
– волновая аберрация, f (Px′, P′) – зрачковая функция. |
|||
|
|
|||||
|
|
|
λ |
|
|
|
В выражении (9.2.2) учитывается одновременно ограничение пучков и наличие аберраций.
Зрачковая функция (pupil function, PF) показывает влияние оптической системы на прохождение электромагнитного поля от точки предмета до выходного зрачка и в общем случае в канонических координатах описывается выражением:
12 |
(ρx , ρy ) e |
2πiW (ρx ,ρy ) |
|
|
|
|
|
|
, внутри Ω0 |
(9.2.3) |
|
f (ρx , ρy )= τ |
|
|
|||
|
|
|
|
|
|
0, вне Ω0 |
|
|
|
|
|
где (ρx , ρy ) – |
канонические зрачковые координаты, τ(ρx , ρy ) – |
||||
функция пропускания по зрачку, |
Ω0 – область зрачка в канонических |
||||
координатах. |
|
|
|
|
|
Теперь нужно перейти от поля на выходном зрачке к полю на изображении. Вблизи изображения геометрическая оптика не применима, поэтому для описания поля на изображении следует использовать теорию дифракции.
U ′(Px′,Py′)
(x′p , y |
′p ) |
r′ |
rp′ = const
выходная
сфера
y′ |
U (x, y) |
|
′ |
(x′, y′)
x′
z′
плоскость
изображения
Рис.9.2.2. Формирование комплексной амплитуды в плоскости изображения.
Для вычисления комплексной амплитуды поля в плоскости изображения применим принцип Гюйгенса в форме интеграла Гюйгенса-Френеля. Рассматриваемая область находится вблизи центра выходной сферы (рис.9.2.2):
|
|
|
|
′ |
′ |
|
||
|
|
|
2πi |
n r |
|
|
|
|
′ ′ ′ |
′ ′ ′ |
e |
λ |
|
|
′ |
(9.2.4) |
|
|
|
|
||||||
|
|
|
|
|||||
|
|
|
|
|
||||
U (x , y |
)= ∫∫U (xp , yp ) |
|
r′ |
|
|
dSp |
||
|
S ′p |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
135

Используя зрачковую функцию, выражение (9.2.4) можно записать в виде:
|
|
|
|
|
|
|
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
2πi |
r n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∫∫ f (ρx , ρy ) |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U (x , y |
)= |
|
|
λ |
|
|
|
dρxdρy |
|
|
|
|
|
|
|
|
(9.2.5) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
′ ′ ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
′ |
|||
|
|
|
r′ = rp′ + |
|
r′ и |
|
|
r′ |
|
<< rp′, |
|
|
e2πi |
r n |
|
|
|
||||||||||||||
Поскольку |
|
|
|
|
|
то |
множитель |
|
λ |
|
|
можно |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
′ ′ |
|
|
|
|
|
|
r′ n′ |
|
|
′ ′ |
|
|
|
|
r′ |
n′ |
||||||||
|
|
|
|
2πi |
r n |
|
|
|
|
|
2πi |
p |
|
|
2πi |
r n |
|
|
2πi |
p |
|
|
|
||||||||
представить в |
виде e |
λ |
= e |
λ |
e |
λ . |
Множитель |
e |
λ = const , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
следовательно его можно вынести за интеграл, и не учитывать, так как нас интересует только относительное распределение комплексной амплитуды. Тогда выражение (9.2.5) преобразуется так:
|
|
|
|
2πi |
′ |
′ |
|
|
|
|
|
||
|
|
)= ∫∫ f (ρx , ρy ) |
e |
r n |
|
|
|
|
|
|
|
||
′ |
′ ′ |
|
λ |
|
dρxdρy |
|
(9.2.6) |
||||||
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||
U (x , y |
|
r′ |
|
|
|
||||||||
′ |
|
|
|
′ |
′ |
|
′ |
′ |
|
||||
можно выразить через |
и |
(рис.9.2.3). |
|||||||||||
r |
x |
, y |
|
xp |
, yp |
||||||||
|
y′ |
|
r′ |
А′ |
|
rp′ |
|
|
|
|
|
σ ′p |
О′ |
z′ |
|
r′ |
|
плоскость выходная изображения сфера
Рис.9.2.3. Связь r′ с радиусом выходной сферы rp′ и расстоянием r′ от выходной сферы до точки A′.
|
|
′ ′ |
′ ′ |
Отрезок OA = |
r′ ≈ − |
x xp + y yp |
|
|
|||
|
|
|
rp′ |
а для остальных лучей: n′x′p = ρx A′, rp′
записать так:
, причем n′sinσ′A = A′ – для крайнего луча,
n′y′p = ρy A′. Теперь интеграл (9.2.6) можно rp′
|
|
|
|
′ |
′ |
|
|
|
|
|
|
−2πi |
x ρx + y ρ y |
A′ |
|
||
′ ′ ′ |
)= ∫∫ f (ρx , ρy ) |
e |
|
λ |
|
|||
|
|
|
dρxdρy |
(9.2.7) |
||||
|
|
|
|
|||||
|
|
|
|
|
||||
U (x , y |
|
|
|
r′ |
|
|||
|
|
|
|
|
|
|
|
|
136

Введем канонические (приведенные) координаты на предмете и изображении:
|
|
A |
|
ηx′ |
= −x′ |
|
Ax′ |
|
|||
ηx = −x |
|
x |
|
|
|
|
|
|
|
||
|
|
|
|
λ |
|
||||||
|
λ |
|
|
(9.2.8) |
|||||||
|
|
A |
|
η′y |
= −y′ |
|
A′y |
||||
ηy = −y |
|
y |
|
|
|
|
|
|
|||
|
|
|
λ |
|
|||||||
|
λ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
Тогда в канонических координатах получим: |
|
||||||||||
|
|
|
|
′ |
′ |
ρ y )dρxdρy |
(9.2.9) |
||||
U ′(ηx′,η′y )= ∫∫ f (ρx , ρy ) e2πi(ηx ρx +ηy |
|||||||||||
Так как зрачковая функция вне зрачка равна нулю, интегрирование происходит внутри зрачка. Комплексная амплитуда в изображении точки в канонических координатах, как следует из выражения (9.2.9), связана со
зрачковой функцией через обратное преобразование Фурье: |
|
U ′(ηx′,η′y )= F −1[f (ρx , ρy )] |
(9.2.10) |
Комплексная амплитуда поля в изображении точки есть обратное Фурьепреобразование от зрачковой функции в канонических координатах.
Функция рассеяния точки – это распределение не амплитуды поля, а интенсивности, то есть квадрата модуля комплексной амплитуды U′(ηx′,η′y )2 . Тогда для ФРТ можно получить следующее выражение:
|
|
|
h(ηx′,η′y )= |
|
F −1[f (ρx , ρy )] |
|
2 |
(9.2.11) |
|||||||||||
|
|
||||||||||||||||||
|
|
|
Оптическую передаточную функцию также можно выразить в |
||||||||||||||||
|
|
||||||||||||||||||
канонических координатах: |
|
||||||||||||||||||
|
|
|
D(ωx ,ωy )= F[h(ηx ,ηy )] |
(9.2.12) |
|||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
где ωx ,ωy – канонические пространственные частоты: |
|
|||||||||||||||
|
|
|
ω |
|
= −ν |
|
|
λ |
= −ν′ |
|
λ |
= ω′ |
|
||||||
|
|
|
x |
x |
|
|
|
′ |
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|||||
|
|
|
|
|
|
|
|
Ax |
|
Ax |
|
|
|
|
|||||
|
|
|
ωy = −ν y |
|
λ |
= −ν′y |
λ |
=ω′y |
(9.2.13) |
||||||||||
|
|
|
|
A |
A |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
y |
|
|
|
|
|||
Канонические частоты безразмерные: линмм sinмм . В этих координатах
получаем простую связь зрачковой функции с оптической передаточной функцией:
D(ωx ,ωy )= F |
|
F −1 |
[f (ρx , ρy )] |
|
2 |
|
(9.2.14) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
137
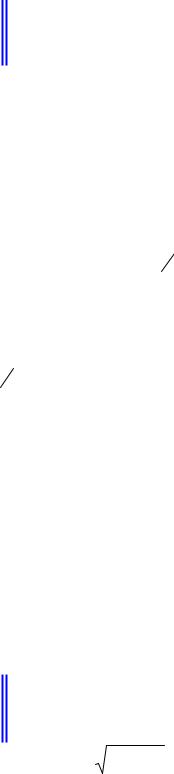
Это выражение в соответствии со свойством преобразования Фурье можно представить через автокорреляцию зрачковой функции:
D(ωx ,ωy )= |
1 |
∫∫ f (ρx , ρy ) f * (ρx −ωx , ρy −ωy ) dρx dρy |
(9.2.15) |
Ω |
|||
0 |
|
|
|
где Ω0 – площадь зрачка в канонических координатах.
9.3.Дифракционная структура изображения
9.3.1.Функция рассеяния точки в случае отсутствия аберраций
Предположим, что в оптической системе аберрации отсутствуют W (ρx , ρy )= 0 . Тогда зрачковая функция оптической системы в соответствии с
выражением (9.2.3) будет выглядеть следующим образом:
|
|
12 |
(ρx , ρy ), внутри Ω0 |
|
f0 |
|
|
(9.3.1) |
|
(ρx , ρy )= τ |
|
|||
|
|
|
0, внеΩ0 |
|
|
|
|
|
где Ω0 – область зрачка в канонических координатах.
Будем считать, что пропускание равномерно по зрачку, то есть τ 12 (ρx , ρy )=1. Тогда, поскольку в канонических координатах зрачок всегда круглый, выражение (9.3.1) можно записать следующим образом:
|
|
при |
2 |
2 |
)≤1 |
|
f0 (ρx , ρy )= |
1, |
(ρx |
+ ρy |
(9.3.2) |
||
0, |
при |
(ρ2 |
+ ρ2 )>1 |
|||
|
|
|
x |
y |
|
|
То есть зрачковая функция равна единице в пределах круга, и нулю на всей остальной области, и следовательно, математически описывается при помощи функции Circ(ρx , ρy ):
f0 (ρx , ρy )= Circ(ρx , ρy ) |
(9.3.3) |
Чтобы получить функцию рассеяния точки при отсутствии аберраций, нужно взять обратное преобразование Фурье от безаберрационной зрачковой функции, то есть от функции Circ(ρx , ρy ):
h (ρ |
|
, ρ |
|
)= |
|
F −1[Circ(ρ |
|
, ρ |
|
)] |
|
2 = |
|
J1 |
(2πη) 2 |
= Bessinc2 (η) |
(9.3.4) |
|
|
|
|
|
|
|
|||||||||||||
x |
y |
|
x |
y |
|
|
|
|
||||||||||
0 |
|
|
|
|
|
|
|
|
|
πη |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ηx2 +ηy2 , J1 (2πη ) |
|
|
|
|
||||||||||
где |
η = |
|
– |
функция Бесселя первого |
рода, первого |
|||||||||||||
порядка.
Картина ФРТ для безаберрационной оптической системы (рис.9.3.1) состоит из центрального максимума диаметром 1.22 канонических единиц и побочных максимумов – колец с шагом, постепенно приближающимся к 0.5 канонических единиц. Безаберационная ФРТ симметрично относительно оптической оси. Центральный максимум содержит 83.8% всей энергии (его
138
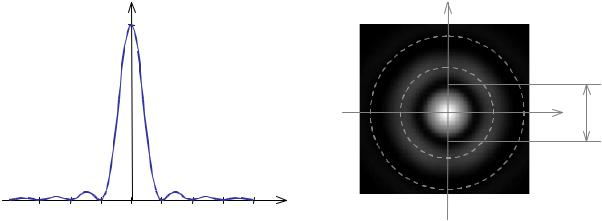
высота равна единице), первое кольцо – 7.2% (высота 0.0175), второе 2.8% (высота 0.0045), третье 1.4% (высота 0.0026), четвертое 0.9%.
h0 (η) |
ηy |
|
|
1.0 |
|
|
|
|
ηx |
1.22 |
λ |
|
|
Ay |
|
|
η |
|
|
-1.62 -1.12 -0.61 0 0.61 1.12 |
1.62 |
|
|
а) сечение |
б) общий вид распределения |
|
|
|
интенсивности (картина Эри) |
|
|
Рис.9.3.1. Функция рассеяния точки в отсутствие аберраций.
Центральный максимум ФРТ называется диском Эри (Airy). Диаметр диска Эри в реальных координатах на изображении:
D = |
1.22λ |
|
(9.3.5) |
|
|
||||
|
|
A0′ |
|
|
|
′ |
– апертура осевого пучка. |
|
|
где A0 |
|
|||
Диск Эри в общем случае может быть не круглым, если меридиональная A′y и сагиттальная Ax′ апертуры различны.
Из выражения (9.3.5) следует, что поскольку апертура для изображения ближнего типа не может быть больше показателя преломления, изображение точки для ближнего типа не может быть меньше длины волны.
9.3.2. Влияние неравномерности пропускания по зрачку на ФРТ
На рис.9.3.2 показан вид ФРТ для различных функций пропускания. Если пропускание уменьшается к краям зрачка (2), то центральный максимум ФРТ расширяется, а кольца исчезают. Если пропускание увеличивается к краям зрачка (3), то центральный максимум сужается, а интенсивность колец увеличивается. Эти изменения по-разному влияют на структуру изображения сложного объекта, и, в зависимости от требований, используются различные функции пропускания, “накладываемые” на область зрачка. Это явление называется аподизацией.
139
