1. Определение комплексных чисел.Алгебраическая форма комплексного числа. Действия над комплексными числами в алгебраической форме.

Комплексным числом z будем называть упорядоченную пару (a, b)

действительных чисел a, b ∈ R, условно записываемую в виде:

z = a + ib, a, b ∈ R,

при этом число a называется действительной частью числа z и обозначается a = Re (z),

число b называется мнимой частью числа z и обозначается b = Im (z), а символ i

называется мнимой единицей.

Множество всех комплексных чисел обозначается символом C.

Если мнимая часть числа z есть ноль, т.е. z = a + i · 0, то число z считают действительным,

совпадающим с a ∈ R, а если z = 0 + ib, то число z называют чисто мнимым.

Действия над комплексными числами:

• Сравнение

 означает, что  и  (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

• Вычитание

• Умножение

• Деление

2. Модуль и аргумент комплексного числа.Умножение и деление комплексных чисел в тригонометрической форме.

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа  обозначается  и определяется выражением . Часто обозначается буквой . (r=mad z= |z|)

Аргументом числа  -  это угол  (в радианах) радиус-вектора точки, соответствующей числу , называется  и обозначается .

z=x+iy=|z|(cosφ+isinφ) – тригонометрическая форма записи комплексного числа.

3. Извлечение корня из комплексного числа.

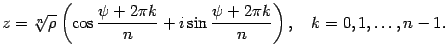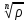, – арифметический корень из модуля числа z, а Ψ – одно из значений Arg z. Из основной теоремы алгебры следует, что корни n-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного n-угольника, вписанного в окружность радиуса  с центром в нуле.

4. Определители второго и третьего порядка. Свойства определителей. Определитель n-го порядка.

Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: 

Определителем третьего порядка называется следующее выражение: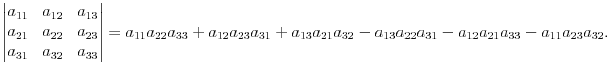

Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной из противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус.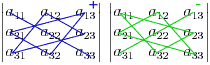 

Свойство 1. Определитель не меняется при транспонировании.

Это означает, что определитель матрицы равен определителю транспонированной матрицы (матрицы, в которой строки заменены соответствующими столбцами).(m×n=n×m)

Исходя из первого свойства, в остальных свойствах мы можем говорить только о строках, подразумевая, что эти свойства применимы также и к столбцам.

Свойство 2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

(это свойство вытекает из свойства 5 при k=0)

Свойство 3. От перестановки двух строк определитель меняет свой знак.

Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю.

Пусть ∆ - определитель матрицы с двумя одинаковыми строками. Если эти строки переставить местами, то определитель должен поменять знак. Но так как строки одинаковы, то определитель не изменится. Т.е. имеет ∆=-∆, откуда 2∙∆=0 или ∆=0.

Свойство 5. Если все элементы некоторой строки умножить на некое число, то сам определитель умножится на это число.

.

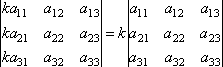Свойство 6. Определитель, содержащий две пропорциональные (одинаковые) строки, равен нулю.

(свойство 5, а затем свойство 4)

Свойство 7. Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей.

.
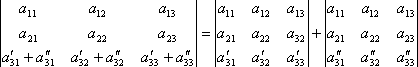