Кривая Безье (элементарная)

Теорию кривых Безье разработал П. де Кастело в 1959 году и, независимо от него, П. Безье в 1962 году. В общем случае кривая Безье — это частный случай В-СПЛАЙНОВ (NURBS-кривых), которые можно определить как взвешенная сумма п+ 1 контрольных точек, где весовыми коэффициентами являются полиномы Бернштейна.

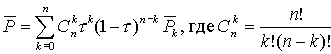
Рассмотрим определения первых трех степеней кривой Безье.

Линейная кривая, кривая первой степени (прямая), определяется следующей параметрической формулой:

B(t) = (1 - t)P₀+t P₁ где 0 < t < 1.

Это выражение представляет собой линейную интерполяцию между двумя точками.

Квадратичная кривая, кривая второй степени, определяется формулой:

B(t) = (1 - t)²P₀ + 2(1 - t)tP₁ + t²P₂ где 0 < t < 1.

Квадратичные кривые Безье используются, например, в шрифтах TrueType при определении контуров символов.

В графике используется кубическая кривая, кривая третьей степени, которая определяется формулой:

B(t) = (1 - t)³Р₀ + 3(1 - t)²tP₁ + 3(1 - t)t²P₂ + t³Р₃ где 0 < t < 1.

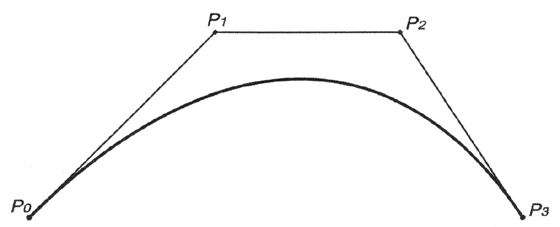
Четыре опорные точки P₀, P₁, P₂ и P₃, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P₀ направляясь к P₁ и заканчивается в точке P₃ подходя к ней со стороны P₂. То есть кривая не проходит через точки P₁ и P₂, они используются для указания её направления. Длина отрезка между P₀ и P₁ определяет, как скоро кривая повернёт к P₃.

В декартовых координатах это означает:

X(t) = (1 - t)³X₀ + 3(1 - t)²tX₁ + 3(1 - t)t²X₂ + t³X₃

Y(t) = (1 - t)³Y₀ + 3(1 - t)²tY₁ + 3(1 - t)t²Y₂ + t³Y₃.

Для прямого построения кривой задаемся конкретным значением параметра t в диапазоне от 0 до 1 и подставляем в формулы. Получаем координаты x и y одной точки на кривой. Затем задаемся следующим значением параметра t и получаем координаты x и y следующей точки на кривой. И так далее.

В матричной форме кубическая кривая Безье записывается следующим образом:

,

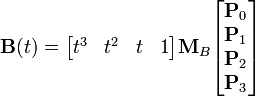где называется базисной матрицей Безье:

.

В современных графических системах, таких как PostScript, Metafont и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых.

Построение кривых Безье

Линейные кривые

Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P₀ до P₁ находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P₀ и P₁. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P₀ и P₁.

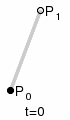
Построение отрезка

Квадратичные кривые

Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q₀ и Q₁ из условия чтобы параметр t изменялся от 0 до 1:

Точка Q₀ изменяется от P₀ до P₁ и описывает линейную кривую Безье. Q₀ = (1 - t)P₀+t P₁

Точка Q₁ изменяется от P₁ до P₂ и также описывает линейную кривую Безье. Q₁ = (1 - t)P₁+t P₂

Точка B изменяется от Q₀ до Q₁ и описывает квадратичную кривую Безье. B(t) = (1 - t)Q₀+t Q₁

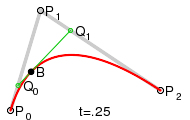
Построение квадратичной кривой Безье

Кубические кривые

Для кубической кривой строятся промежуточные точки Q₀, Q₁ и Q₂, описывающие линейные кривые, а также точки R₀ и R₁, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0

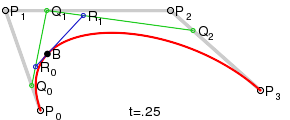
Построение кубической кривой Безье