3 Формирование дистанционного цифрового управления в режиме «online»

Исходные данные для формирования ДЦУ в режиме «online»:

1. Объект управления: непрерывный ТО с передаточной функцией:

, где;

2. канал связи: двоичный, с пропускной способностью ;

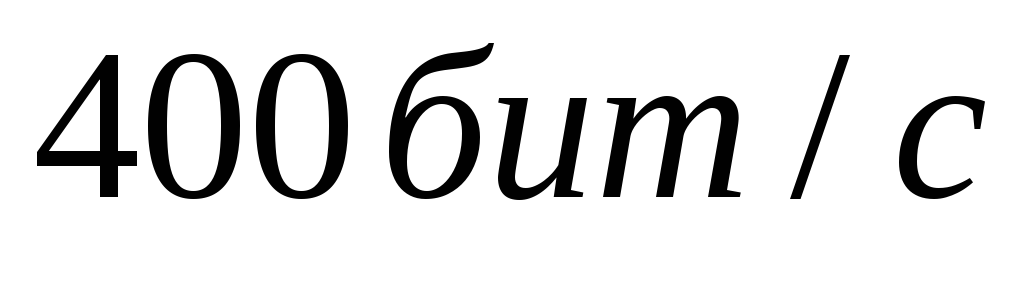3. вероятность искажения элементарного сигнала двоичного кода передачи управления по прямому каналу и кода сигналов измерения выхода по обратному каналу: ;

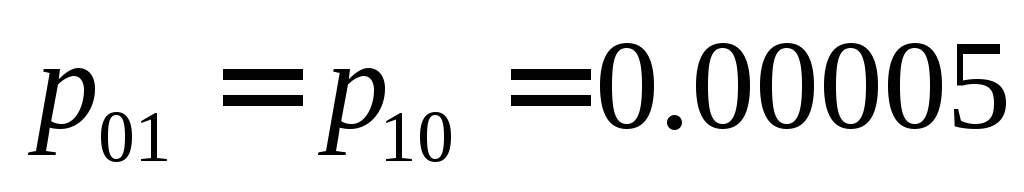4. число разрядов ЦАП и АЦП: ;

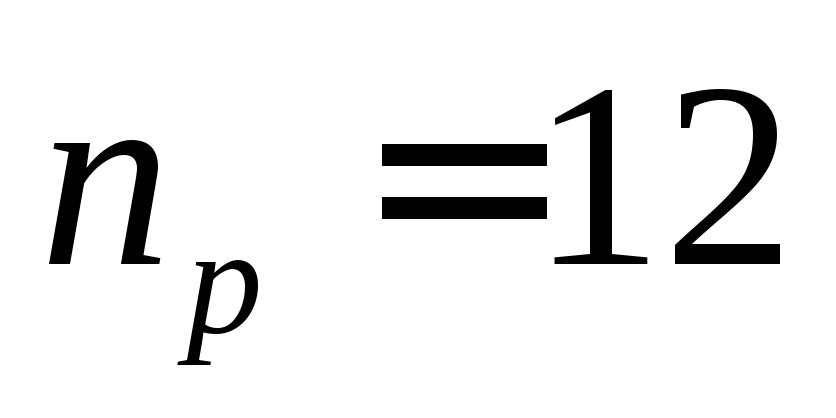5. перерегулирование: ;

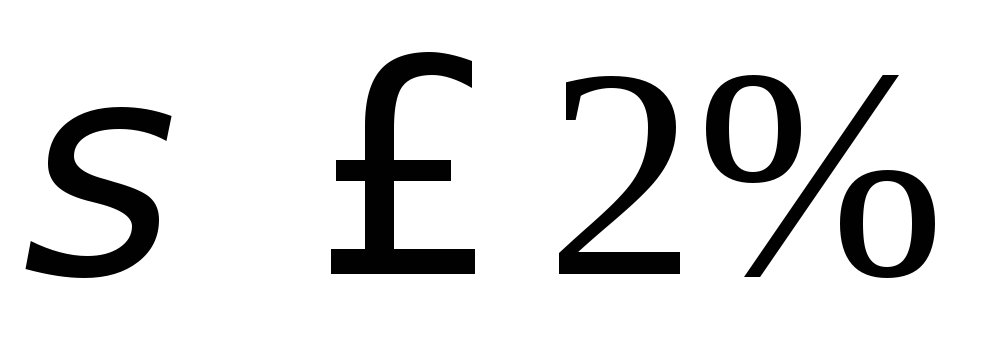6. время переходного процесса: ;

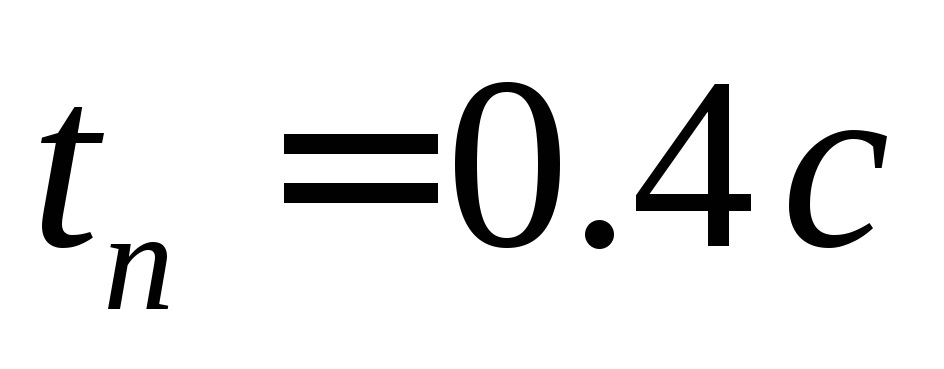7. добротность по скорости: ;

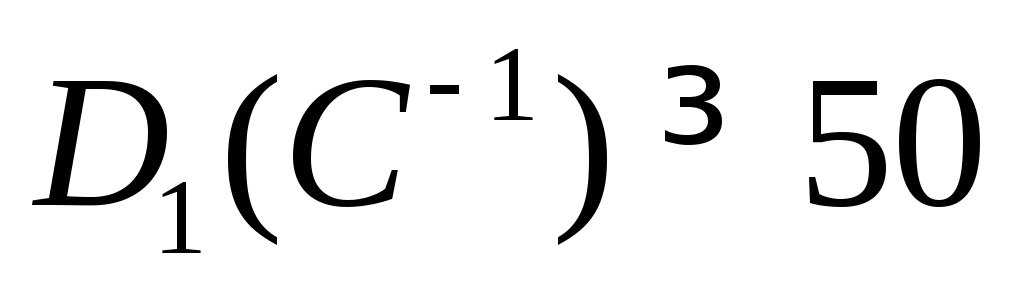8. характер помехозащиты: произвольный;

9. категория системы передачи – приема ТМ – информации III-я с допустимой вероятностью ошибочного приема.

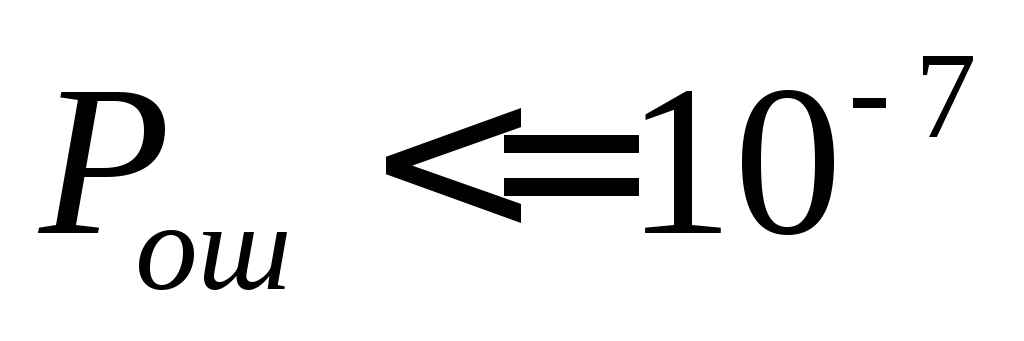После подстановки получим:

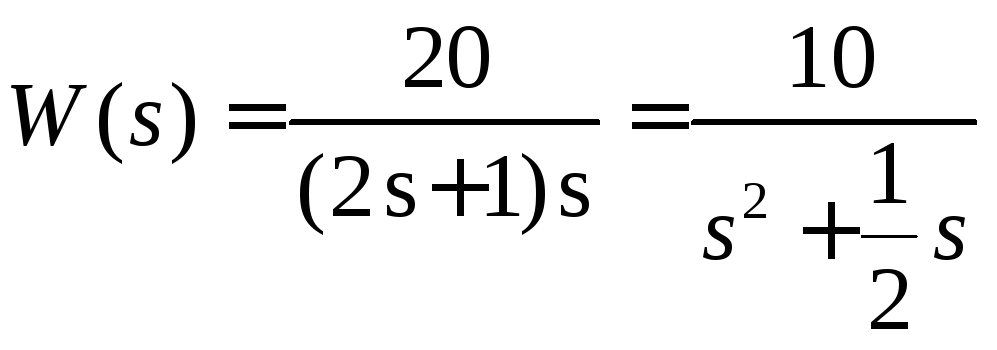(3.1)

Представим данную модель в канонической управляемой форме ВСВ:

(3.2)

где

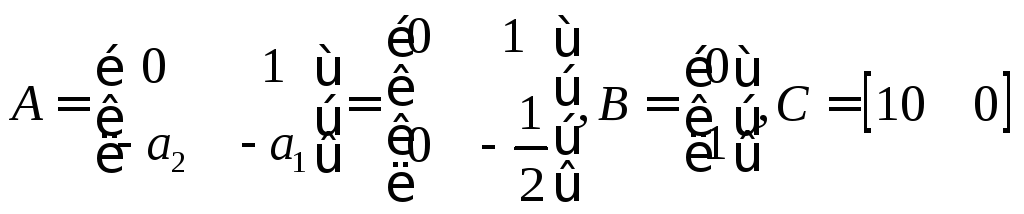
Проверим управляемость непрерывного ОУ:

(3.3)

Так как , следовательно объект полностью управляем.

Проверим наблюдаемость непрерывного ОУ:

(3.4)

Так как , следовательно объект полностью наблюдаем.

Сформируем формат помехозащищённого кода при заданном числе разрядов информационной части.

Для данного случая получим:

(3.5)

Введем в рассмотрение первую априорную рабочую гипотезу о том, что достаточно, чтобы формируемый ПЗК исправлял ошибки только первой кратности (s=1).

(3.6)

Проведем проверку справедливости гипотезы:

(3.7)

(3.8)

Условие не выполняется, поэтому переходим ко второй рабочей гипотезе: достаточно, чтобы код исправлял ошибки первой и второй кратности (s=2).

(3.9)

(3.10)

Проведем проверку справедливости второй рабочей гипотезы:

(3.11)

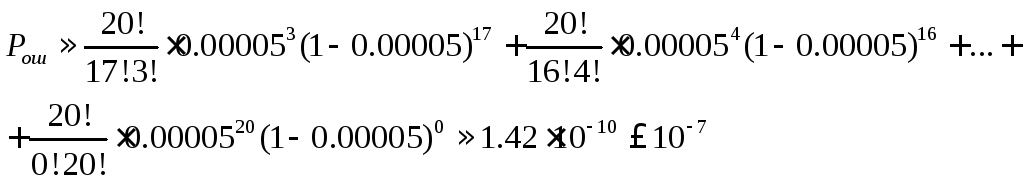(3.12)

Условие выполняется, поэтому параметры помехозащищённого когда в форме.

Рассчитаем длительность передачи одного бита , используя данное значение пропускной способности канала связи.

(3.13)

Теперь сформируем модифицированной интервал дискретности, расширенный на величину числа проверочных разрядов помехозащищённого кода:

(3.14)

Для синтеза динамического цифрового управления, перейдем к дискретному представлению. Дискретную форму запишем в виде:

(3.15)

где матрицы находятся по формулам:

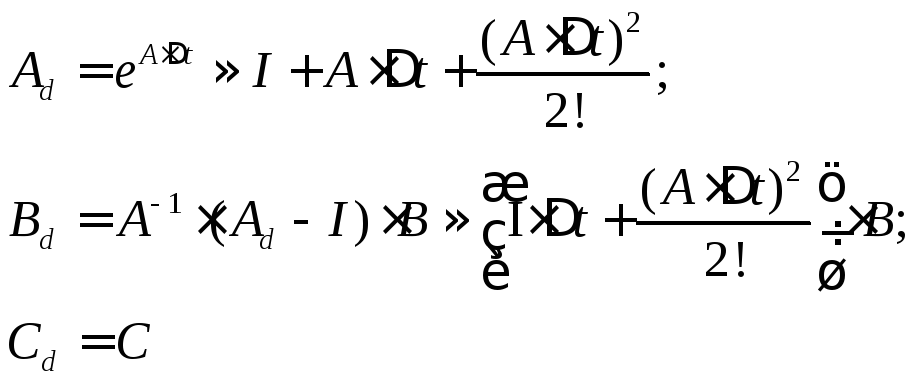(3.16)

Тогда получим:

Построим дискретное модельное представление прямого и обратного каналов связи в виде дискретных систем первого порядка, осуществляющих задержку дискретного сигнала на один интервал дискретности агрегированной длительности в форме:

(3.17)

где ,– соответственно векторы состояния, управления и выхода в прямом и обратном каналах единичной размерности так, что справедливы представления

(3.18)

Сформируем дискретное модельное представление агрегированного, составленного из последовательного соединения прямого канала связи, дискретного ТО и обратного канала связи с вектором состояния размерности na=n+2, вектором регулируемого выходатехнического объекта цифрового дистанционного управления, вектором измеряемого выхода, представляющим собой выход ОКС, и матрицами, в форме

;

, (3.19)

где

;;;;

;;;

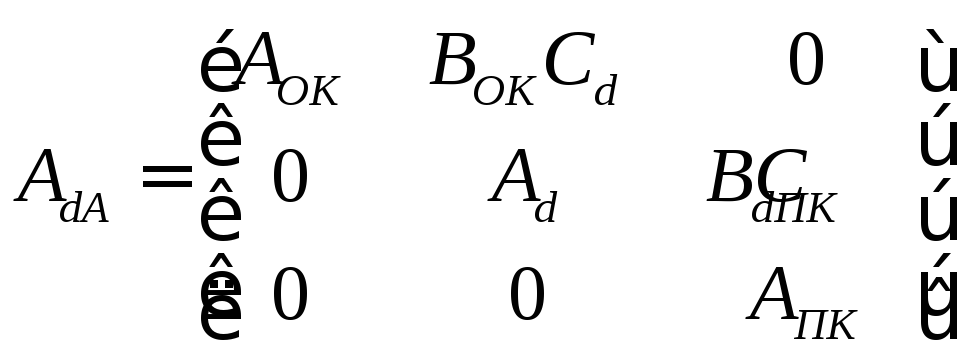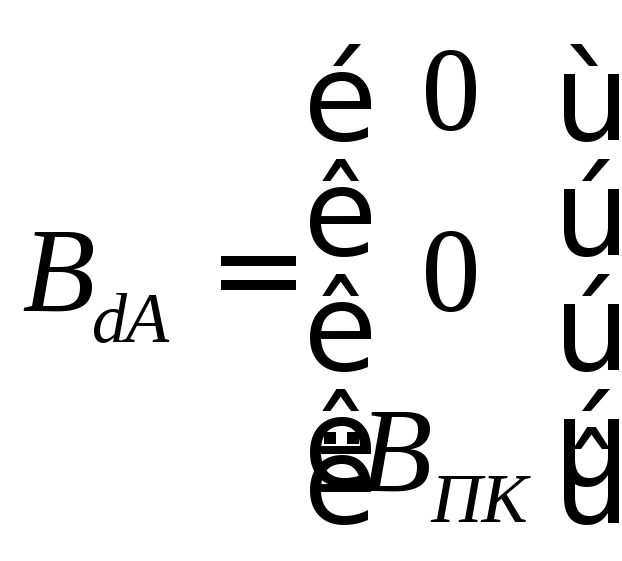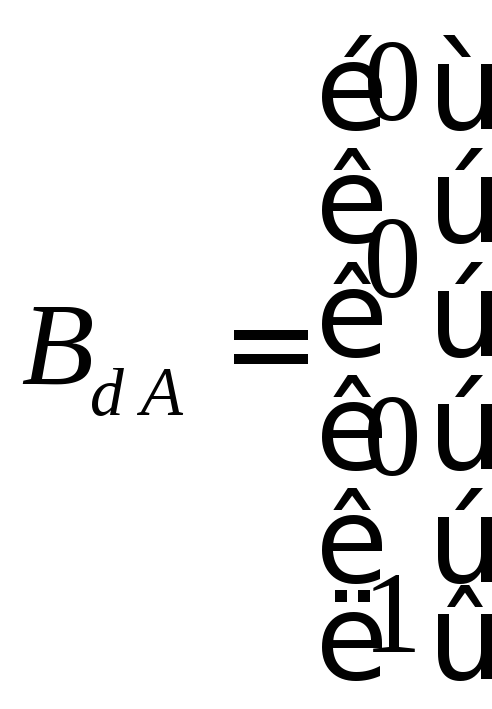Требование по обеспечению добротности по скорости означают, что система должна обладать астатизмом (отрабатывать постоянное воздействие с нулевой установившейся ошибкой).

Для построения регулятора необходимо выбрать непрерывную полиномиальную модель желательного поведения системы из условия, что данная модель будет обеспечивать время переходного процесса , добротностьи перерегулирование. Также необходимо выполнение условия т. Шеннона-Котельникова:

,(3.20)

Выберем биномиальное распределение мод 4-ой степени:

(3.21)

Для биномиального распределения мод:

;(3.22)

Проверим выполнимость условия т. Шеннона-Котельникова:

(3.23)

Условие т. Шеннона-Котельникова не выполняется, то есть невозможно обеспечить заданную добротность с учетом того, что интервал дискретности . Таким образом, для решения поставленной задачи необходимо предложить заказчику уменьшить добротность.

Поставим следующую задачу: необходимо выбрать непрерывную полиномиальную модель желательного поведения системы из условия, что данная модель будет обеспечивать время переходного процесса и добротность. Тогда для биномиального распределения мод:

;(3.24)

Возьмем большую характеристическую частоту. Тогда:

(3.25)

т.е. условие т. Шеннона-Котельникова выполняется. Характеристический полином:

. (3.26)

Зададим матрицу с данными модами:

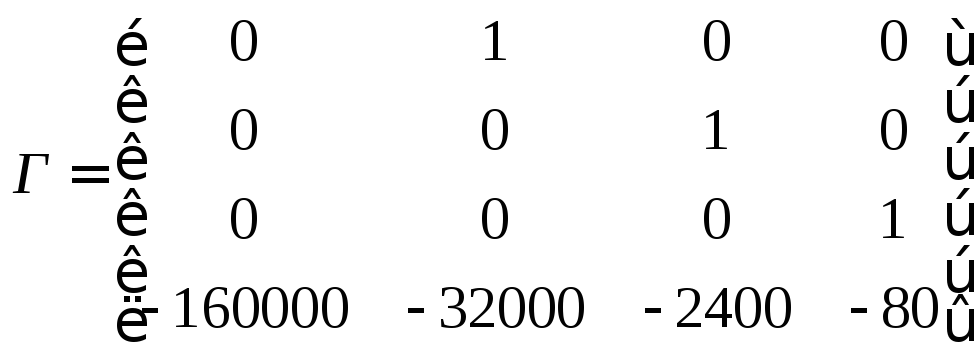(3.27)

и матрицу из условия наблюдаемости пары

. (3.28)

Дискретизируем данную модель:

. (3.29)

Матрицу назначим из условия наблюдаемости пары:.

Найдем матрицу из уравнения Сильвестра, а затем и матрицу обратных связей из условия:.

(3.30)

Система представима в виде:

,

где.

Вычислим матрицу :

(3.31)

Сформируем матрицу прямой связи по вектору задающего воздействияна основании требований к свойствам отношения «вход-выход» проектируемой дискретной системы, обязательным из которых является равенство входа и выхода при неподвижном положении, так что выполнение последнего позволяет записать

(3.32)

Матрица 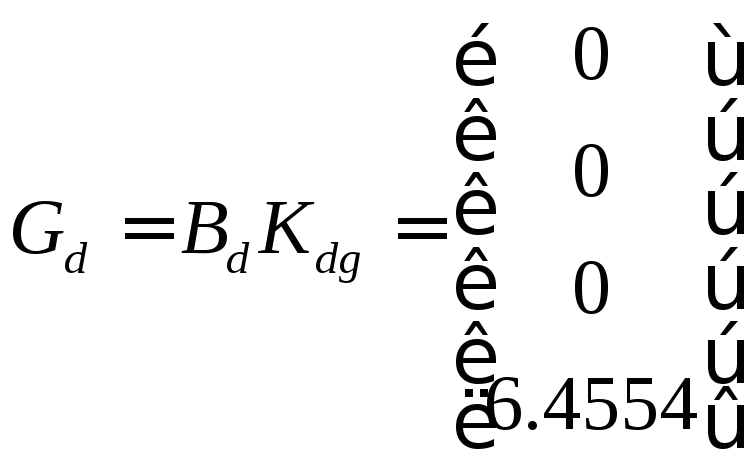(3.33)

Проведем исследование динамических свойств спроектированной дискретной системы. Схема моделирования системы представлена ниже (см. рисунок 3.1)

Рисунок 3.1 – Схема моделирования системы

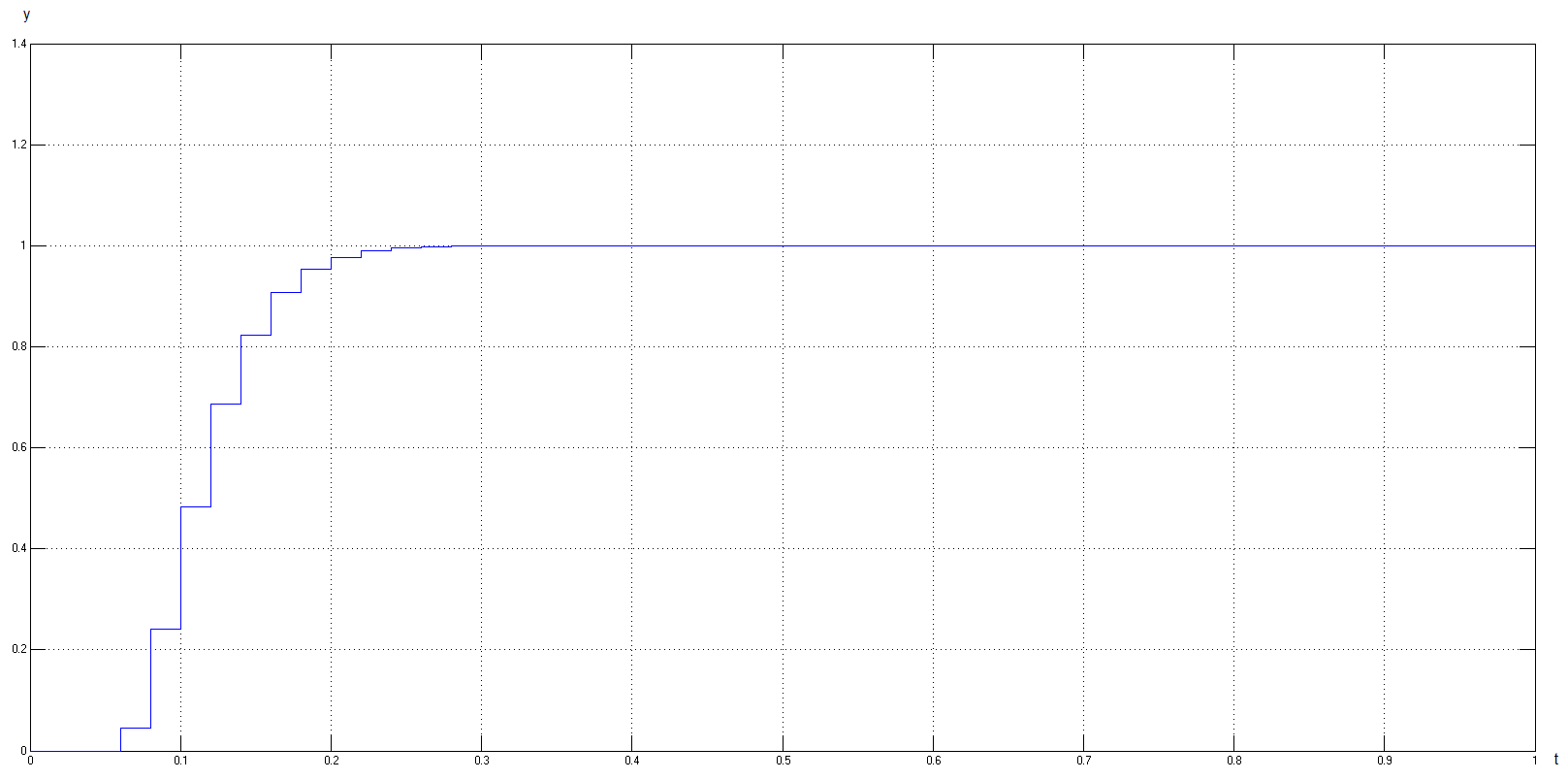
Рисунок 3.2 – График переходного процесса при единичном воздействии

Из рисунка 3.2 видно, что время переходного процесса и величина перерегулирования находятся в допустимых приделах:

В результате моделирования разработанной системы управления НТО можно сделать вывод, что динамические свойства системы удовлетворяют требованиям технического задания.

Откажемся от гипотезы о полной измеримости задающего воздействия , перейдя к форме, использующей доступный непосредственному измерению сигнал ошибкии единичную отрицательную связь по выходу для формирования сигнала управления в виде:

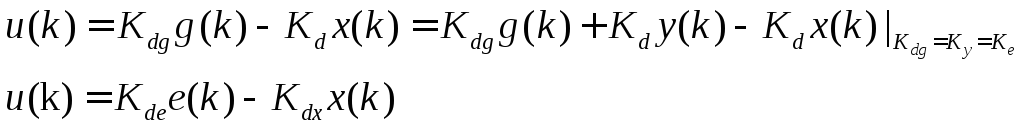(3.34)

где матрица вычисляется с помощью соотношения:

(3.35)

В реальной системе нам недоступен для измерения вектор состояния объекта, так что заменим его оценкой, формируемой наблюдающим устройством, задаваемым в форме:

(3.36)

где матрицы Дну выбираются из условия

(3.37)

где - знак мажоризации, означающий в данной задаче, что моды матрицы состояния наблюдателя локализованы на комплексной плоскости в круге меньшего радиуса, чем радиус круга локализации мод матрицысостояния дискретной системы.

(3.38)

Зададим моды матрицы состояния: , и матрицу состояния наблюдателя в форме Жордана:

(3.39)

Матрица строится из условия управляемости наблюдателя:

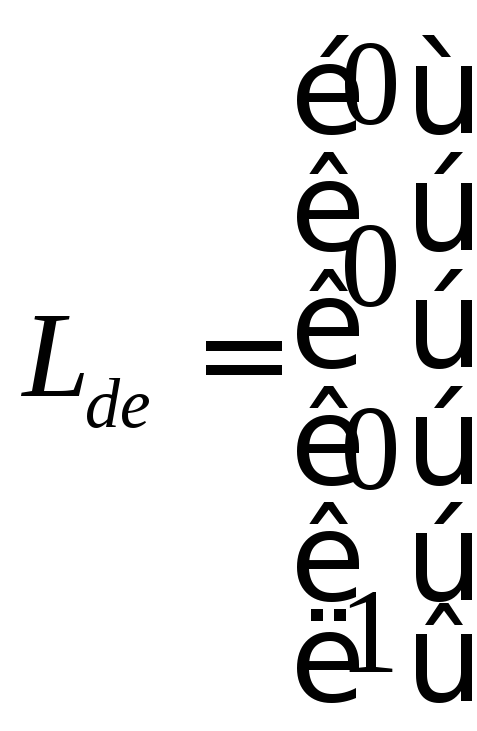(3.40)

Вычислим матрицы подобия вектора наблюдениявектору состояния, задаваемого в форме:

(3.41)

в силу решения матричного уравнения Сильвестра:

(3.42)

которое позволяет сформировать матрицу входа в форме:

(3.43)

что обеспечивает асимптотическую сходимость к нулю вектора невязки наблюдения в форме:

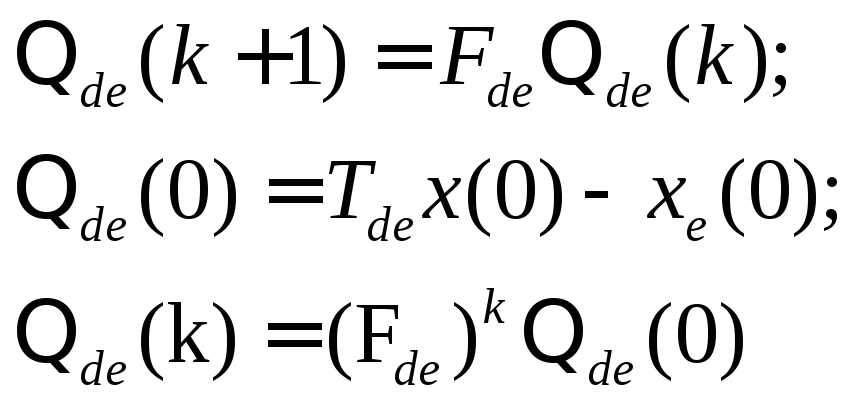(3.44)

Матрица имеет вид:

(3.45)

Матрица входа :

(3.46)

Сформируем физически реализуемую динамическую версию исходного закона управления в форме:

(3.47)

где матрицы связей по выходу объекта управления ипо вектору состояния динамического наблюдающего устройства, вычисляется в силу матричного равенства:

(3.48)