
Актуальность
Актуальность данной рассматриваемой темы очень хорошо просматривается, т. к. канторовская теория применима в большом спектре научных областей: информатике, химии и др.
Теория Георга Кантора
Основные понятия теории частично упорядоченных множеств:
Определение и примеры
Предпорядки
Частично упорядоченное множество P=‹P,
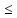 ›
-основные
понятия
›
-основные
понятияОсобые элементы
Ранжирование частично упорядоченных множеств.
Порядковые гомоморфизмы
Идеалы и фильтры
Конусы
Точные грани
Определение и примеры
Определение:
Пару ,
где
,
где - непустое множество, а
- непустое множество, а - рефлексивное, антисимметричное и
транзитивное бинарное отношение на
нем, часто называютчастично
упорядоченным множеством( сокращенно
ч.у. множеством)
- рефлексивное, антисимметричное и
транзитивное бинарное отношение на
нем, часто называютчастично
упорядоченным множеством( сокращенно
ч.у. множеством)
Рефлексивность
(R) : ;
;
Антисимметричность:
(AS):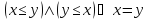
Транзитивность(T):
Примеры:
 - классический пример ч. у. множества(
упорядочивание множеств по включению,
- классический пример ч. у. множества(
упорядочивание множеств по включению,
 и
и - два упорядочивания одного множества
- два упорядочивания одного множества
Предпорядки
Рассмотрим данную тему сразу на примере:
Пример:
Пусть
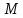 - множество людей,
- множество людей,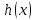 - рост, а
- рост, а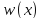 – вес человека. Определим на отношение
– вес человека. Определим на отношение на
на :
: Является ли
Является ли отношением частичного порядка на
отношением частичного порядка на
Ответ: Нет.
т.к.
 – рефлексивно и транзитивно, но не
является антисимметричным отношением:
– рефлексивно и транзитивно, но не
является антисимметричным отношением: (могут
найтись два человека с одинаковым ростом
и весом)
(могут
найтись два человека с одинаковым ростом
и весом)
Отношения
со свойствами ( и
и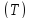 называются предпорядками.
называются предпорядками. .
.
Частично упорядоченное множество P= (P,
 - основные понятия:
- основные понятия:
Если
 ,
то
,
то и
и сравнимы
сравнимы иначе они несравнимы
иначе они несравнимы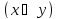
Полный (линейный) порядок, если

Если в
 нет ни одной пары различных сравнимых
элементов, то это тривиально упорядоченное
множество
нет ни одной пары различных сравнимых
элементов, то это тривиально упорядоченное
множество непосредственно предшествует
непосредственно предшествует непосредственно следует за
непосредственно следует за если
если
 - интервал
- интервал
 - цепь
- цепь ,
а совокупность попарно несравнимых
элементов – антицепь в
,
а совокупность попарно несравнимых
элементов – антицепь в .
.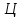 епь
максимально( насыщенная), если при
добавлении к ней любого элемента она
перестает быть цепью
епь
максимально( насыщенная), если при
добавлении к ней любого элемента она
перестает быть цепью -
двойственный к
-
двойственный к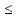 порядок:
порядок:
Частично упорядоченные множества: особые элементы
Определение:
элемент
 ч. у. множества
ч. у. множества называют:
называют:
Максимальным, если

Минимальным, если

Наибольшим, если

Наименьшим, если

Для любых
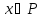
Элемент наибольший, если все другие элементы содержатся в нем, и он минимальный, если нет элементов , содержащих его ( аналогично для наименьшего и минимального элементов.






1

2
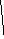




Наибольший(1) и наименьший(0) –граничные элементы. В конечном частично упорядоченном множестве имеется как минимум по одному максимальному и минимальному элементу
Ранжирование частично упорядоченных множеств
Цепное условие Жордана - Дедекинда: Все максимальные цепи между двумя данными элементами локально конечного ч.у. множества имеют одинаковую длину.
Если ч. у.
множество удовлетворяет условию Жордана
– Дедекинда и имеет наименьший элемент
0 , то оно ранжируемо, т. е. на нем можно
определить функцию ранга


 и такое множество имеет слои
и такое множество имеет слои


-----
-









-
-
Если множество ранжируемо, то любой его слой( ноне только) является антицепью.
Порядковые гомоморфизмы
Определение:
Отображение
 носителей ч. у. множеств называется
соответственно
носителей ч. у. множеств называется
соответственно
Изотонным( монотонным, порядковым гомоморфизмом) если

Обратно изотонным, если

Антиизотонным, если

Если
 изотонно, обратно изотонно и инъективно,
то это вложение или (порядковый)
мономорфизм ( символически
изотонно, обратно изотонно и инъективно,
то это вложение или (порядковый)
мономорфизм ( символически )
)
Cюръективный мономорфизм
- ( порядковый) изоморфизм ( символически )
)
Изоморфизм ч.у. множества в себя - (порядковый) автоморфизм
Идеалы и фильтры частично упорядоченных множеств
Определение:
Подмножество
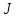 элементов ч.у. множества
элементов ч.у. множества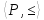 называется его ( порядковым) идеалом,
если
называется его ( порядковым) идеалом,
если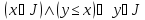
Подмножество
 элементов
элементов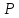 называется его (порядковым) фильтром,
если
называется его (порядковым) фильтром,
если
∅ и все
множество
 –
порядковые идеалы. Важное свойство:
объединение и пересечение порядковых
идеалов есть порядковый идеал.
–
порядковые идеалы. Важное свойство:
объединение и пересечение порядковых
идеалов есть порядковый идеал.
Обозначение:
 - множество всех порядковых идеалов
частично упорядоченного множества
- множество всех порядковых идеалов
частично упорядоченного множества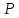 .
.
Конусы
Определение:
Пусть
 - ч.у. множество и
- ч.у. множество и .
Множества
.
Множества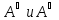 .
.
 И
И

Называют
верхними и нижними конусами множества
 ,
а их элементы – верхними и нижними
гранями множества
,
а их элементы – верхними и нижними
гранями множества соответственно. Для одноэлементного
множества
соответственно. Для одноэлементного
множества
Понятно,
что если

 идеал,
а
идеал,
а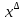 - фильтр
- фильтр – такие идеалы и фильтры называют
главными
– такие идеалы и фильтры называют
главными
Конечнопорожденный
идеал:

Точные грани
Определение:
Пусть
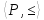 - ч. у. множество и
- ч. у. множество и .
.
Наименьший элемент в
 называется точной верхней границей
гранью множества
называется точной верхней границей
гранью множества
Наибольший элемент в
 называется точной нижней гранью
множества
называется точной нижней гранью
множества
Пример: (sup Aи/или inf A могут и не существовать)
 ,но
множество
,но
множество
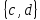 не имеет инфимума⇒
sup
не имеет инфимума⇒
sup отсутствует.
отсутствует.
 отсутствует inf
отсутствует inf [2]
[2]


c d
a b
Применение частично упорядоченных множеств на практике
Частично упорядоченное множество - один из типов бинарного отношения. Отношение частичного порядка является одним из фундаментальных общематематических понятий и широко используется в теоретической математике, в системах логического вывода и во многих других приложениях. Оно является обобщением таких широко известных бинарных отношений как "меньше или равно" (Ј) для чисел и "включено или равно" (Н) для множеств. Обозначение "Ј" часто используется не только для обозначения отношения "меньше или равно" на множестве чисел, упорядоченных по величине, но и для обозначения произвольного отношения частичного порядка[3]. А так же для создания графов, решения задач с помощью ч.у. множеств и многое другое. Как мы видим, спектр применения частично упорядоченных множеств довольно широк.
