ДискретнаяМатематика / Student Solutions Manual / chapter 4

21. (b) By de nition F (F 1 (B1)) B1 regardless of whether F is onto.

(() Suppose F is onto, and let y 2 B1. Then there is an element x 2 A

such that F (x) = y. Then, x 2 F 1(B1) by de nition, so y = F (x) = y: then x 2 F 1(B1) by de nition, so y = F (x) 2 F (F 1(B1)). Thus, B1 F (F 1(B1)) whence B1 = F (F 1(B1)):

()) Let y 2 B: Then F (F 1(fyg)) = fyg: Therefore, F is onto.

23. An operation on a set Y is called commutative if for all y; z 2 Y , y z = z y: For X and FX as de ned in Exercise 22, Prove that need not be commutative on FX .

23. De ne F (1) = 1; F (2) = 3; F (3) = 2; G(1) = 2; G(2) = 1; G(3) = 3: Then F and G do not commute with respect to composition, since (F G)(1) = F (2) = 3 but G F (1) = G(1) = 2, for example.

4.7 Exercises

1.Prove that in any set of 27 words, at least two must begin with the same letter assuming at most a 26 letter alphabet.

1. Map the set of words to the letters of the alphabet by taking each word to its rst letter. Since there are 27 words and 26 letters the Pigeon-Hole Principle says that at least two words are mapped to the same letter.

3.Prove that in any class of more than 101 students, at least two students must receive the same grade for an exam with grading scale of 0 to 100.

3. Map the class onto the set of possible grades by assigning each student his or her grade. Apply Theorem 2. Or,

102+

101

2

5. Prove that in any class of 35 students, at least seven receive the same nal grade, where the scale is A-B-C-D-F.

5.

35

5

= 7

7. There are 35,000 students at State University. Each student takes four di erent courses each term. State University o ers 999 courses each term. The largest classroom on campus holds 135 students. Is this a problem? If so, what is the problem?

7. The total number of enrollments is 140,000. The average class size, by the Generalized Pigeon-Hole Principle, is

140; 000 1

999

+ 1 = 141:

Since 141 > 135; the average class will not t in any classroom!

9.Suppose someone (say Aesop) is marking days in some leap year (say 2948). You don't know which days he marks, only how many. Use this to answer the following questions. (Warning: Some, but not all, of these questions use the Pigeon-Hole Principle.)

(a)How many days would Aesop have to mark before you can conclude that he marked two days in January?

(b)How many days would Aesop have to mark before you can conclude that he marked two days in February?

(c)How many days would Aesop have to mark before you can conclude that he marked two days in the same month?

(d)How many days would Aesop have to mark before you can conclude that he marked three days in the same month?

(e)How many days would Aesop have to mark before you can conclude that he marked three days with the same date (for example, the third's of three di erent months, or the 31sts of three di erent months)?

(f)How many days would Aesop have to mark before you can conclude that he marked two consecutive days (for example, January 31 and February 1)?

(g)How many days would Aesop have to mark before you can conclude that he marked three consecutive days?

9. (a) Assume the year is not a leap year. (a) 366 - 29 = 335

9. (b) 366-26 = 338

9. (c) 13

9. (d) 25

9. (e) n 1 + 1 = 3. The answer is 63.

31

9. (f) 184

9. (g) Consider 122 distinct 3-tuples consisting of the dates of three consecutive days. The rst set will contain 1, 2, and 3 representing January 1, 2, and 3. Map the days chosen to these sets. We would like to know when one of these sets is the image of three elements in the domain. We would like to nd n such that the Generalized Pigeon-Hole Principle gives a value of 3 for the expression: + 1: n must be at least 245.

11. There are ve suburbs of the city of Melbourn. How many all-stars must be picked from the suburbs to guarantee at least ve players come from the same suburb?

11.

m 1

5

+ 1 = 5

gives m = 21:

13. A man has 10 black socks and 11 blue socks scrambled in a drawer. Still half asleep the man reaches in the drawer to get a pair of matching socks. How many socks should he select, one at a time, before he will be sure that he has a matching pair. How many selections are needed to be sure he has a blue pair?

13.

m 1

2

+ 1 = 2

gives m = 3: Clearly the answer you expect. To get a pair of a particular color you may draw all the socks of the other color before you get the two required of a speci c color.

15.Construct a sequence of 16 integers that has no increasing or decreasing subsequence of ve elements.

15.4-3-2-1-8-7-6-5-12-11-10-9-16-15-14-13

17.A widget-maker makes at least one widget every day, but not more than

730widgets in a year. Given any n, show that the widget-maker makes exactly n widgets in some set of consecutive days. For some n, it may take more than a single year.

17. De ne two strictly increasing sequences of elements. The rst has ai = the number of widgets made in the rst i days and let bi = n + ai for 1 i 2921 n: The two sets have 5842 n integers in them with the largest being no bigger than 8 n 730 = 5840 n: Therefore, there is at least one member common to both sets.

and G : Y ! N be one-to-one functions. Then, de ne H1 : X [ Y ! N as H1(z) = 2F (z) if z 2 X and H1(z) = 2F (z)+1 if z 2 X Y . H2 : X \Y ! N as H2(z) = F (z). H3 : X Y ! N as H3(z) = F (z): t is easy to prove that H1; H2, and H3 are one-to-one. Also, de ne H4 : X Y ! N N as H4(x; y) = (F (x); G(y)). It is easy to see that H4 is 1{1, so we have jX Y j jN Nj. A proof similar to the proof of Theorem 7 shows that jN Nj = jNj> So, by Theorem 1(b), jX Y j jNj.

5. (b) X [ Y and X \ Y must be countably in nite. X \ Y and X Y could be nite as in the case of

X = f2 i : i 2 Ng

and

Y= f2 i + 1 : i 2 Ng

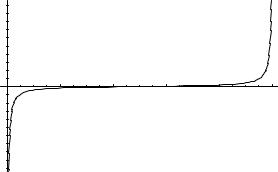
7.Prove that the function de ned as F : (0; 1) ! R de ned as F (x) = (1=2 x)=(x(1 x)) is a bijection.

7.

From the graph of the function it is clear that this is a 1-1 and onto function as required.

9.Prove Theorem 1.

9. Theorem 1(a) Use the identity function.

Theorem 1(b) The composition of 1-1 functions is 1-1 by Theorem 5 of the rst section of this chapter.

Theorem 1(c) Use the identity function.

Theorem 1(d) The inverse of a 1-1 onto function is 1-1 and onto.

Theorem 1(e) The composition of bijections is a bijection.

11.A chain letter scheme is a famous (and usually illegal) get-rich-quick scheme. A person X receives a letter with, say, ve names on it. X sends $10 to the person whose name is at the top of the list. X then deletes that name from the top of the list, adds his or her own name to the bottom of the list, and sends the letter to ve \friends," all within one day. In around two weeks, X is supposed to receive $31,250.

Suppose every person who receives the letter obeys the instructions (including sending $10 to the person listed rst!). Show that, if there are onlynitely many people, the scheme cannot work (in some sense of \cannot work" which you should make precise). Show that, if there are countably in nitely many people, the scheme can work.

11. Let X be the nite set of people to send and receive letters. Suppose j Z j = n and 5m n < 5m+1: At t = 1 there is one player sending 5 letters. At t = 2 the ve players who received letters from the person at t = 1 must send letters to 52 new players. At t = i the 5i 1 players who received letters from the 5i 2 players at time t = i 1 must send letters to 5i new players. Since the universe only holds between 5m and 5m+1 players for some m, after round m + 1 the 5m players who received letters at t = m must send 5m+1 letters to new people and there are not enough new players to continue the procedure. If there are in nitely many players, the game can continue inde nitely.

13.Challenge: Show that j R j = j P(N) j. (Hint: Use the Cantor-Schr•oder- Bernstein Theorem. To show that j R j j P(N) j, you might use function D : R ! P(Q) where for r 2 R; D(r) = fq 2 Q : q < rg.)

13. One answer can be found by proving that between any two real

numbers there is a rational number. Suppose r and s are real numbers. If jr sj 1, it is clear that there is an integer between them and the conclusion holds. If jr sj < 1, then it is not so easy. Let

r= c:c1c2c3c4 : : : cn : : : and s = c:c1c2c3c4 : : : dn : : : where the nth decimal place is the rst decimal place in which the two numbers di er. If

r> s, then let rational wanted = c:c1c2c3c4 : : : dn50000000 : : : : Clearly rational wanted is a rational number and it is between r and s.

The following solution was found in Discrete Mathematics in Computer Science by Donald F. Stanat and David F. McAllister published by Prentice Hall in 1977.

(() We show that jPN)j jRj by constructing an injection as follows:

g : P(N) ! [0; 1]

For every subset S N, g maps S to a real fraction,

g(S) = :x0x1x2 : : :

where the fraction is expressed in binary representation and

x2j = 0 for j = 0; 1; 2; : : :

x2j+1 = 1 for j 2 S; and = 0 for j 62S

e.g., g(;) = 0; g(N) = :0101010101 : : : ; g(f1; 3; 5g) = :000100010001 : : :

(Note that we cannot use (in place of g) the function g0 such that g0(S) is the binary fraction :x0x1x2 : : : ; where xj = 1 if j 2 S and xj = 0 if j 62S: Since the value of g0(S) is expressed as a binary fraction, the function g0 is not an injection from P(N) to the [0, 1]: for example, the sets f0g and fn : n 2 N ^ n > 0g would be mapped to .1000. . . and .0111. . . respectively; in the binary number system, these are di erent representations of the same fraction. However, if g0(S) is speci ed to be a ternary (base 3) fraction, then the same characterization of g0 will specify an injective function.)

()) We show jRj jP(Nj by constructing an injection from [0, 1] to P(N): Let x = x0x1x2 : : : be a binary representation of x 2 [0; 1]: (If x does not have a unique representation, choose one arbitrarily.) De ne f (x) to be the set such that j 2 f (x) if and only if xj = 1; e.g., f (0) = ;; f (1) = f (:111 : : :) = N; f (:101010000 : : :) = f0; 2; 4g: Then f is an injection. (Note that f is not a surjection. For example, if .1000. . . is chosen as the representation of 1/2 rather than .0111. . . , then the set f0g will be the image of f but the set fn : n 2 N ^ n > 0g will not.)

It follows from the Cantor-Schr•oder-Bernstein Theorem that jP(N)j = jRj:

15. Show that there are in nite sets

X0; X1; X2; : : : ; Xk; Xk+1; : : :

where for each k 2 N, jXk j < jXk+1j.

15.

j N j < j P(N) j < j P(P(N)) j <

The solution rests on the assumption that j A j < j P(A) j Since any element x 2 A can be associated with fxg 2 P(A), it follows that jAj < jP(A)j: Assume there is a bijection A ! P(A). So each x 2 A is associated with a subset Sx of A. Now, de ne the subset

S = fx 2 A : x 62Sxg

Since S is a subset of A, our assumed bijection tells us that there must be an element y in A that is associated with S. In other words Sy = S for some y 2 A: A contradiction arises by trying to gure out if y is an element of Sy or not.

17.(a) Show that the set of all nite sequences of elements of the one element set f0g is countably in nite.

(b)Show that the set of all nite sequences of elements of the two element set f0,1g is countably in nite.

(c)Challenge: Show that the set of all nite sequences of natural numbers is countably in nite. (Hint: Use a diagonal argument.)

17. (a) For each n there is one sequence consisting of n 0's. The map from N to the nite sequences of 0's is obvious.

17. (b) For each n there are 2n sequences of length n consisting of 0's and 1's. For n list the 2n sequences as 0, 1, . . . , 2n 1 and map them to the consecutive integers starting at 2n.

17. (c) For each n 2 N the nite sequences of length n can be identi ed with N n. For each n such a set is countable. All these sets are countably many countable sets and so are countable.

4.10 End of Chapter Materials

Starting to Review

1.Which of the following are functions?

(i)X is the set of students at Purdue University. For x 2 X, de ne g(x) to be the oldest brother of x

(ii)X is the set of governors of Oregon. For x 2 X, de ne g(x) is the year that x was rst sworn into o ce as governor.

(iii)For x 2 R, de ne g(x) = x=j x j

(a)(i)

(b)(ii)

(c)(iii)

(d)None of the above 1. b

3.Let X = f11; 12; 23; 44g and Y = fr; s; t; vg be sets. De ne the following subsets of X Y :

F1 = f(11; r); (44; v); (12; s); (23; t)g F2 = f(23; s); (11; v); (44; t); (12; s)g F3 = f(44; t); (12; s); (23; s); (11; v)g

Which of the sets F1; F2, and F3 are onto functions?

(a)F1; F2; F3

(b)F2; F3

(c)F1; F3

(d)F1; F2

3.c

5.For n = 0; 1; : : : ; 10, list the values of the following functions de ned recursively.

(a) function s(n) if n = 0 then

return (0)

else

return (2n + s(n 1))

(b)function p(n) if n = 0 then

return (1)

else

return (n p(n 1))

(c)function d(n)

if n = 10 then return (100)

else

return (d(n + 1) 10)

5. (a) 2, 6, 12, 20, 30, 42, 56, 72, 90, 110

(b) 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3828800

(c)100, 90, 80, 70, 60, 50, 40, 30, 20, 10, 0

7.Let F and G be the functions de ned on f1, 2, 3, 4, 5g as follows: