
ДискретнаяМатематика / Student Solutions Manual / chapter 2
.pdf
7.Write the following condition in an if...then with the negations incorporated into the conditions themselves:
If NOT ((x < 3) OR (Y > 2)); then
7. If ((x 3) and (y 2)) then
9.Using the conjunctive normal form, identify values for which the statement
:(:(p _ q) ^ (:p _ q))
is true.
9. The CNF is p _ q. p _ q is true whenever one of p and q is true. All possible truth values except the case that both p = F and q = F make the statement T .
Review Questions
1.Construct a truth table for the statement :(p _ q) _ :(p ^ q):
1.
|
p |
q |
A = :(p _ q) B = :(p ^ q) A _ B |
|
||
|
T |
T |
F |
F |
F |
|
|
T |
F |
F |
T |
T |
|
|
F |
T |
F |
T |
T |
|
|
F |
F |
T |
T |
T |
|
|
|
|
|
|
|
|
3. For which truth values does the following formula
:(p _ :q)
have a truth value T ?
3.
|
p |
q |
:q p _ :q :(p _ :q) |
|
||
|
T |
T |
F |
T |
F |
|
|
T |
F |
T |
T |
F |
|
|
F |
T |
F |
F |
T |
|
|
F |
F |
T |
T |
F |
|
|
|
|
|
|
|
|
The answer is p = F and q = T
5.6 Use the substitution rule that p ! q for p, and prove that the result is a tautology for
:q ! (q ! p)
6. Solution Required
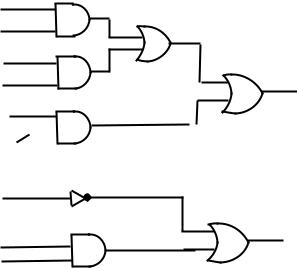
7.Draw combinatorial circuits that realize the following:
(a)(p ^ q) _ (q ^ r) _ (p ^ :r)
(b):((p ^ q) _ p) _ (p ^ q)
7.(a)
p q
q
r
p
r


7.(b)
p
p
q
Using Discrete Mathematics in Computer Science
1.We built up formulas with the logical operators ^, _, :, !, $, and constants T and F . In designing circuits, we described gates for only three connectives: ^, _, and :. Computer hardware designers might want to make as few kinds of gates as possible. Do they really need a ! gate? (The answer turns out to be \no"; how do you know that?) Could they get along with fewer than three types of gates? A set of logical operators is called complete if every well formed formula of propositional logic is equivalent to a well formed formula using connectives from the set.
(a)Find a formula equivalent to a ! (b ^c ^d) using only the connectives : and ^ (and not the constants T and F ). Find the shortest such formula; does it have more or fewer symbols than the formula a ! (b ^ c ^ d)?
(b)Show that the set f:; ^g of operators is complete.
(c)Find a formula equivalent to a ! (b^c^d) using only the connectives : and ! (and not the constants T and F ). Find the shortest such formula; does it have more or fewer symbols than the formula a ! (b ^ c ^ d)?
(d)Show that the set f:; !g of operators is complete.
(e)Find a formula equivalent to a ! (b ^ c ^ d) using only the connective
!and the constant F . Find the shortest such formula; does it have more or fewer symbols than the formula a ! (b ^ c ^ d)?
(f) Show that the set fF; !g is complete. 1. (a) :(a ^ :(b ^ c ^ d))
1. (b)
a _ b |
= |
::(a _ b) |
|
= |
:(:a ^ :b) |
a ! b |
= |
:a _ b |
|
= ::(:a _ b) |
|
|
= |
:(::a ^ :b) |
|
= |
:(a ^ :b) |
1. (c)
a ! (b ^ c ^ d) $ |
a ! (::(b ^ c) ^ d) |
$ |
a ! (:(:b _ :c) ^ d) |
$ |
a ! (:(b ! :c) ^ d) |
$ |
a::(:(b ! :c) _ :d) |
$ |
a ! (::(b ! :c) _ :d) |
$ |
a ! :((b ! :c) _ :d) |
$ |
a ! :(:(b ! :c) ! :d) |
1. (d) a _ b = :a ! b) a ^ b = :(:a _ :b) = :(a ! :b)
1.(e)a ! (((b ! (c ! F )) ! F ) ! (d ! F )) ! F )
1.(f)
:a $ a ! F a _ b $ :a ! b
a ^ b $ (a ! (b ! F )) ! F

3. The connective if-then-else is de ned by the following truth table:
|
p |
q |
r |
if p then q else r |
|
|
T |
T |
T |
T |
|
|
T |
T |
F |
T |
|
|
T |
F |
T |
F |
|
|
T |
F |
F |
F |
|
|
F |
T |
T |
T |
|
|
F |
T |
F |
F |
|
|
F |
F |
T |
T |
|
|
F |
F |
F |
F |
|
|
|
|
|
|
|
This connective is key in binary decision diagrams (BDD), which provide one standard way for manipulation of propositional formulas in computer programs. For example, BDDs have been widely used by computer chip designers in showing that the circuits in the chips they design match the speci cations for those chips. (In BDD language, the connective is often called just IT E.)
(a)Find a formula equivalent to
if a then
if b then c else d
else
if e then d else c
using only the connectives ^, _, and :.
(b)Find a formula equivalent to
if a then
if b then c else d
else
if e then d else c
in CNF.
(c)Find a formula equivalent to :a using only the if-then-else connective and constants T and F .
(d)Find a formula equivalent to (a _ b _ c) ^ (:a _ :b _ d) ^ (:c _ :d) using only the if-then-else connective and constants T and F .
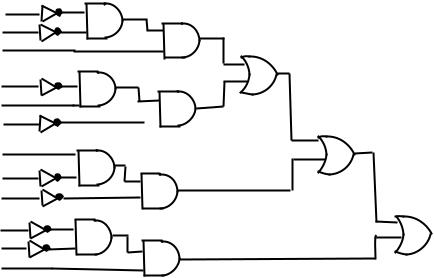
3.(a) (a ^ ((b ^ c) _ (:b ^ d))) _ (:a ^ ((e ^ d) _ (:e _ c))).
3.(b) (:a _ :b _ c) ^ (:a _ b _ d) ^ (a _ :e _ d) ^ (a _ e _ c)
3.(c) if a then F else T
3.(d) Following tradition with BDD's, we choose to consider the variables
in the natural order, a; b; c; d. Tradition also has a \test" (x in if x then
. . . ) which is always as single proposition letter; the syntax of course allows the \test" x to be complex if-then-else expression (or T or F too).
if a |
|
|
|
then |
|
|
|
if b |
|
|
|
then |
|
|
|
if c then F else d |
|
|
|
else |
|
|
|
if c then |
if d then F else T |
else |
T |
else |
|
|
|
if b |
|
|
|
then |
|
|
|
if c then |
if d then F else T |
else |
T |
else |
|
|
|
if c then |
if d then F else T |
else |
F |
5.Find a DNF for the condition that there are an odd number of 1's in the three binary strings p; q; and r. Draw a combinatorial network to represent the disjunctive normal form. Can you simplify the combinatorial circuit using the properties of a boolean algebra?
5. (:p ^ :q ^ r) _ (:p ^ q ^ :r) _ (p ^ :q ^ :r) _ (:p ^ :q ^ :r)
p q
r
p q r
p q r
p q r
7. Determine if the CNF
(x _ y _ :z _ w _ u _ :v) ^
(:x _ :y _ z _ :w _ u _ v) ^
(x _ :y _ :z _ w _ u _ :v) ^ (x _ :y)
or the CNF
(p _ r _ v) ^ (:p _ r _ v) ^
(p _ :r _ v) ^ (:p _ :r:v) ^
(p _ :r _ :v) ^ (:p _ :r _ :v) ^ (p _ r _ :v) ^ (:p _ r _ :v)
is satis able. This exercise shows that the satis ability problem can be solved if the satis ability problem can be solved for a CNF. The CNF satis ability problem was the rst NP-complete problem.
7. For the rst form use x = T , y = F , z = T , w = T , u = T , and v = T . The second formula is unsatis able.
9. Given an array Names with n elements,
Names[0]; Names[1]; : : : ; Names[n 1];
each containing a surname (family name), the following algorithm nds the largest name (in alphabetical order). Write an invariant for the loop.
temp = Names[0] for i = 1 to n 1
if Names[i] > temp temp = Names[i]
Output temp
9. temp is the largest name in fNames[0], . . . , Names[i]g.
