
ДискретнаяМатематика / Student Solutions Manual / chapter 2
.pdf9. (a) Show that the following formula in CNF is unsatis able:
(p _ q) ^ (p _ :q) ^ (:p _ q) ^ (:p _ :q)
(b) Show that the following formula in CNF is unsatis able:
(p _ q _ r) ^ (p _ :q _ r) ^ (:p _ q _ r) ^ (:p _ :q _ r) ^(p _ q _ :r) ^ (p _ :q _ :r) ^ (:p _ q _ :r) ^ (:p _ :q _ :r)
Can you nd an easier argument than just writing the entire truth table?
(c) Generalize the above to some class of CNF formulas on an arbitrary number n 1 of proposition letters, and prove it by induction on n.
9. (a) If p is T , then the CNF is satis able if q ^ :q is satis able. Since this is not true, the CNF is not satis able. If P is F , then the CNF is satis able if q ^ :q is satis able. Since this is not true, the CNF is not satis able.
9. (b) If p is T , the CNF is satis able if (q _r)^(:q _r)^(q _:r)^(:q _:r) is satis able. By (a) this CNF is not satis able.
If p is F , the CNF is satis able if (q _ r) ^ (:q _ r) ^ (q _ :r) ^ (:q _ r) is satis able. By (a) this CNF is not satis able.
Since the CNF is not satis able when p is either T or F , the CNF is not satis able.
9. (c) For proposition letters p1; p2; : : : ; pn, form all 2n possible clauses in which each pi occurs exactly once | (p1 _p2 _ _pn), (:p1 _p2 _ _pn), (p1 _ :p2 _ _ pn), etc., and let n be the conjunction of all those 2n clauses. We prove by induction on integers n 0 that n is unsatis able.
(Base step) Let n = 0 There is exactly one clause on 0 variables, which is, by de nition, false. 0 asserts that all clauses on 0 variables are true, i.e, that the empty clause is true. So 0 is unsatis able.
(Inductive step) Assume k is unsatis able, and prove that k+1 is unsatis able. For suppose k+1 were satis able. Then some truth assignment I would satisfy k+1 . Either I(pk+1) = T or I(pk+1) = F .
Suppose I(pk+1) = T : Let c be any clause in k . Then c _ :pk+1 is one of the conjuncts of k+1 Since, by assumption, I satis es each clause ink+1 , I satis es c _ :pk+1. Since I(pk+1) = T , I must satisfy c. But then I satis es every clause in k , and thus I satis es k | a contradiction.
Otherwise, I(pk+1) = F , and we get an analogous contradiction.
11.Write pseudocode for a program which, given a formula , nds (i) a logically equivalent formula 0 in CNF and (ii) a logically equivalent formula00 in DNF. The algorithm should be recursive (similar to an induction on formulas) and should not involve the construction of truth tables. Prove the algorithm works. This gives an alternate proof of the theorem that every formula is equivalent to a formula in CNF.
11. We use four functions to nd the CNF form of a formula . A call to CNF(NEGS(IMP( ))) returns an equivalent formula in CNF form.
CNF( )
if is a literal return
elseif 1 ^ 2
return CNF ( 1) ^ CNF ( 2)) else return DIST(CNF( 1 ),CNF(phi2))
DIST( 1; 2)
if 1 01 ^ 001
return DIST( 01; 2) ^ DIST( 001 ; 2) elseif 2 02 ^ 002
return DIST( 1; 02) ^ DIST( 1; 002 ) else return 1 _ 2
NEGS( )
if is a literal return
if ::
return NEGS( ) if 1 ^ 2
return NEGS( 1) ^ NEGS( 2) if 1 _ 2
return NEGS( 1) _ NEGS( 2)
if :( 1 ^ 2)
return NEGS(: 1 _ : 2) if :( 1 _ 2)
return NEGS(: 1 ^ : 2)
IMP( )
if is a literal return
if 1 ^ 2
return IMP( 1) ^ IMP( 2)
if 1 _ 2
return IMP( 1) _ IMP( 2)
if : 1
return : IMP( 1)
if 1 ! 2
return IMP(: 1 _ 2) if 1 $ 2
return IMP(( 1 ! 2) ^ ( 2 ! 1))
De nition. A k-term is a conjunction of k literals. A k-DNF formula is a disjunction of k-terms.
13.(a) Find the resolvant of (p _ q) and (:p _ r) on p.
(b)Find the resolvant of (p _ q _ r _ s) and (:p _ :q _ t) on p.
(c)Find the resolvant of (p _ q) and :p on p.
(d)Find the resolvant of (p) and (:p) on p.
(e)Which resolvant above from parts (a) through (d) is a tautology? Which is tautologically false?
13. (a) q _ :r
13. (b) (q _ r _ s _ :q _ t) 13. (c) q
13. (d) F (the disjunction of 0 literals)
13.(e) (b) is a tautology; (d) is tautologically false.
15.(a) Show that if r is the resolvant of two clauses c1; c2 on proposition letter p, then
fc1; c2g j= r
(Hint: For each interpretation, break into cases, depending on whether p is T or F in each interpretation.)
(b)Prove that if there is a resolution refutation of a set S of clauses, then S is unsatis able. (Hint: Use strong induction on the length of the resolution refutation.)
15.(a) Say, c1 = (p ^ 1 ^ 2 ^ ^ k ) and c2 = (:p ^ 1 ^ 2 ^ ^ m).
So,
r = (p ^ 1 ^ 2 ^ ^ k ^ 1 ^ 2 ^ ^ m)
Let I be any truth assignment which satis es c1; c2. We need to show that I satis es r.
Case 1, I(r) = T : Then, since I satis es c2, I must satisfy at least one of the i's. So I also satis es r.
Case 2, I(r) = F : Then, since I satis es c1, I must satisfy at least one of the j 's. So I also satis es r.
15. (b) Suppose r1; r2; : : : ; rk 1 ; rk = F a set C = fc1; c2; : : : ; cmg of clauses. satis able; let I be any model of C.
is a resolution refutation from Suppose also that C is in fact
Prove by \strong" induction on i that I j= ri. For this, assume that I satis es rj for each j < i and prove that I satis es ri. Break into two cases, depending upon the justi cation for ri in the proof. If ri 2 C, then I satis es ri by assumption. Otherwise, ri is the resolvant of two earlier clauses, rj1 and rj2 . By hypothesis, I satis es rj1 and rj2 . By the previous part, frj1 ; rj2 g j= ri . Thus I satis es ri, as desired.
But now we have that I satis es rk = F , which is impossible. This proves the theorem by contradiction.
2.8 Exercises
Let U = f1; 2; 3; 4g be the universal set for Exercises 1 through 4
1. Rewrite (8x 2 U )P (x) as a conjunction that uses no quanti ers.
1. P (1) P (2) P (3) P (4)
3.Rewrite :(8x 2 U )P (x) as a conjunction that uses no quanti ers.
3.:P (1) _ :P (2) _ :P (3) _ :P (4)
5.For the following predicates with universal set R, state the meaning of the predicate in a sentence. If it is false, give an example to show why. (Example: (8x) (9y) (x < y) says \for every real number, there is a bigger number." This is true.)
(a)(8x)(9y)(x 6= 0 ! xy = a)
(b)(9y)(8x)(x 6= 0 ! xy = 1)
(c)(9x)(8y)(y x)
(d)(8x)(9y)(x + y = x)
(e)(9y)(8x)(x + y = x)
(f)(8x)(8y)(9z)(x < z < y)
(g)(8x)(8y)((x 6= y ! (9z)((x < z < y) _ (x > z > y))
(h)(8x)(8y)(8z)((x > y) ^ y > z) ! x > z)
5.(a) For all nonzero real numbers x there is a real number y such that xy = a where a is some real number. T since a=x is such a number.
5. (b) There exists a real number such that for all real numbers x, if x is nonzero, then xy = 1. F since the existence of y says there is some element and to satisfy the equation we need a di erent y for each nonzero x.
5. (c) There exists a real number x such that for all real numbers y, y is less than or equal x. F since there is no largest real number.
5. |
(d) For all real numbers x there is a real number y such that x + y = x. |
T as y = 0 is such a real number. |
|
5. |
(e) There exists a real number y such that for all real numbers x, |
x + y = x. T as 0 works for y.
5. (f) For all x and all y we can choose a z such that z is between x and y. False for any choice in which y < x.
5. (g) For all x and y if x is not equal to y then we can nd a z that is between x and y if x < y or a z that is between y and x if y < x: T .
5. (h) For all x, y, and z, if x > y and y > z, then x > z. T since this is a familiar property of < in the real number system.
7.For each quanti ed formula that follows: nd a universe U and predicates A and B in which the formula is true, and U; A; and B in which it is false.
(a)(8x)((A(x) _ B(x)) ^ :(A(x) ^ B(x)))
(b)(8x)(8y)(P (x; y) ! P (y; x))
(c)(8x)(P (x) ! (9y)Q(x; y))
(d)(9x)(A(x) ^ (8y)B(x; y))
(e)((8x)A(x) ! (8x)B(x)) ! (8x)(A(x) ! B(x))
7. (a) Let A(x) : x > 2 and B(x) : x < 3
7. (b) Let P (x; y) : x + y = 3
7. (c) Let P (x) : x 2 and Q(x) : 2 < y < x
7. (d) Let A(x) : x > 2 and Q(x; y) : x > 2 and x + y > 3
7.(e) Let A(x) : x 2 and B(x) : x 2 or x < 1
9.For the following formulas, let the universe be R: Translate each of the following sentences into a formula (using quanti ers):
(a)There is no largest number.
(b)There is no smallest positive number.
(c)Between any two distinct numbers, there is a third number not equal to either of them.
9.(a) :9x8y (x > y)
9. (b) :9x8y(x > 0 and y > 0 and x < y)
9. (c) 9z8x8y(x < y and x < z < y) or (y < x and y < z < x)
11.Let U be the set of all human beings living in the year 2001, and translate the following English sentences into quanti ed formulas. Let P (x) stand for \x is young," Q(x) for \x is female," and R(x) for \x is an athlete."
Express symbolically each of the statements:
(a)\All athletes are young"
(b)\Not all young people are athletes"
(c)\All young people are not athletes"
(d)\Some young people are not athletes"
(e)\Some athletes are young females"
(f)\All athletes are young males"
(g)\Some athletes are female and are not young"
(h)\Some young females are not athletes"
(i)\All young females are athlete"s
(j)\Some athletes are not young"
(k)\No young people are athletes"
(l)\All athletes are either female or are young"
(m)\If all athletes are female, then all athletes are young; otherwise, no athletes are young."
11.(a) (8x)R(x) ^ P (x)
11.(b) (9x)P (x) ^ :R(x)
11.(c) (9x)P (x) ^ :R(x)
11.(d) (9x)P (x) ^ :R(x)
11.(e) (9x)R(x) ^ P (x) ^ Q(x)
11.(f) (8x)R(x) ^ P (X) ^ :Q(x)
11.(g) (9x)R(x) ^ Q(x) ^ :P (x)
11.(h) (9x)P (x) ^ Q(x) ^ :R(x)
11.(i) (8x)P (x) ^ Q(x) ^ R(x)
11.(j) (9x)R(x) ^ :P (x)
11.(k) :(9x)P (x) ^ R(x)
11.(l) (8x)R(x) ^ (P (x) _ Q(x))
11.(m)
(8x(R(x) ! Q(x)) ! (8x)(R(x) ! P (x)))^
(:(8x)(R(x) ! Q(x))) ! (8x)(R(x) ! :P (x)))
13.Translate each of the following quanti ed predicates into an English sentence where the universal set is U . Label each as true or false.
(a)(8x)(9y)xy = x
(b)(8y)(9x)xy = x
(c)(8x)(9y)xy = 1
(d)(9y)(8x 6= 0)xy = 1
(e)(9x)(8y)xy = x
(f)(8x 6= 0)(9y)xy = 1
13. (a) for all x there is a y such that xy = x { T as y = 1 works
13. (b) for all y there is an x such that xy = x {T as 0 works
13. (c) this says every x has an inverse-even x = 0 { F as the nonzero property is needed
13. (d) there exists a y such that for all nonzero x that xy = 1 { F this is a case when the other order is true
13. (e) there exists an x such that for all y that xy = x { T as 0 satis es this requirement
13. (f) for all nonzero x there is a y such that xy = 1 { T since this says each nonzero real number has an inverse
15. For any two integers m and n, we say m divides n if there is an integer k such that n = mk. (Many programming languages give easy ways to say that, such as n%m==0 or n div m = 0.) De ne Div(m; n) to be m divides n. Translate each of the following propositions and quanti ed formulas into a clear English sentence. Label each as being true or false; with the universe as the set Z.
(a)Div(5; 7)
(b)Div(4; 16)
(c)Div(16; 4)
(d)Div( 8; 0)
(e)(8m)(8n)Div(m; n)
(f)(8n)Div(1; n)
(g)(8m)Div(m; 0)
(h)(8m)(8n)(Div(m; n) ! Div(n; m))
(i)(8m)(8n)(8p)((Div(m; n) ^ Div(n; p)) ! Div(m; p))
(j)(8m)(8n)((Div(m; n) ^ Div(n; m)) ! m = n)
15. (a) 5 divides 7 { F
15. (b) 4 divides 16 { T
15. (c) 16 divides 4 { F
15. (d) -8 divides 0 { T
15. (e) for all integers m and n we have m divides n { F
15. (f) for all integers n we have 1 dividing n { T
15. (g) for all integers m, m divides 0 { T
15. (h) for all integers m and n if m divides n, then n divides m { F
15. (i) for all integers m, n, and p if m divides n and n divides p, then m divides p { T
15.(j) for all integers m and n, if m divides n and n divides m, then m = n { F
17.Find formulas in negation normal form equivalent to the negations of each of the following:
(a) (8x)(P (x) _ Q(x))
(b) (8x)(8y)(P (x; y) ! Q(x; y))
(c) (8x)((9y)P (x; y) ! Q(x; y))
(d) (8x)((9y)(P (x; y) ! Q(x; y)) ^ (9z)R(x; z))
(e) (9x)((P (x) _ Q(x)) ! R(x))
(f) (8x)(P (x) ! (Q(x) ^ R(x)))
17.(a) (9x)(:P (x) ^ :Q(x))
17.(b) (9x)(9y)P (x; y) ! Q(x; y)
17.(c) (9x)(8y)P (x; y) ! Q(x; y)
17.(d) (9x)(8y)(P (x; y) ! Q(x; y)) ^ (9z)R(x; z))
17.(e) (8x):(:(P (x) _ Q(x) _ R(x))
17. (f) (9x)(8y)P (x) ^ (:Q(x) _ :R(x))
19.Give a universal set U and interpretations to predicates A, B, P , and Q so that each of the following quanti ed formulas is false.
(a)(9xA(x) ^ 9xB(x)) ! (9x(A(x) ^ B(x)))
(b)(8x9yP (x; y)) ! (9x(8yP (x; y)))
(c)(8x(P (x) ! Q(x))) ! ((9xP (x)) ! (8x)Q(x))
(d)8x(:A(x)) $ :(8xA(x))
19. (a) A(x) : x > 3 and B(x) : x < 1
19. (b) P (x; y) : x + y = x
19. (c) P (x) : x 2 and Q(x) : x 2 or x < 1
19.(d) A(x) : x < 2
21.Given an array Values with n elements
Values[0]; Values[1]; : : : ; Values[n 1]
each containing a real number, the following algorithm nds the sum of all the positive values in Values. Write an invariant for the loop.
rollingSum = 0 for i = 0 to n 1
if Values[i] > 0
rollingSum = rollingSum + Values[i] Output rollingSum
21. rollingSum is the sum of all positive numbers among Values[0] through
Values[i].
2.9 End of Chapter Materials
Starting to Review
1.Which of the following are propositions?
(i)\The moon is visible."
(ii)\The property tax rate will increase next year."
(iii)\No one under 18 may buy cigarettes."
(iv)\Please help me with the assignment."
(a)i and iii
(b)i and ii
(c)ii and iii
(d)All of the above
1.b
3.Write the converse, inverse, and contrapositive of the statement \If Sallynishes her work, she will go to the basketball game."
3.converse: If Sally does not nish her work, then she will not go to the basketball game.
inverse: If Sally will go to the basketball game, then she will nish her work.
contrapositive: If Sally will not go to the basketball game, then she will not nish her work.
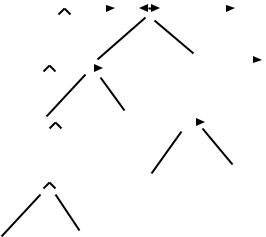
5. What is the truth value that will be computed by the formula represented by the expression tree shown if I(p) = T , I(q) = F , I(r) = T , and I(s) = F in an interpretation I?
|
( |
|
( p |
|
q) |
|
|
r) |
|
|
|
|
(r |
|
s |
) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
(p |
|
q) |
|
|
|
r |
|
|
|
|
|
|
( |
r |
|
s ) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
s |
|
|
|
||||
|
|
|
|
q) |
|
r |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
( p |
|
|
|
|
|
|
|
|
s |
|
||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
p |
|
q |
|
|
r |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
p
5. T
