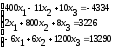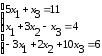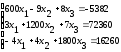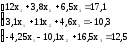3. Метод простой итерации (метод Якоби)

Пусть требуется решить систему линейных уравнений, которая в матричном виде записывается как:

,

где

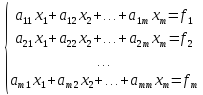(5.7)

Предположим, что диагональные элементы матриц A исходной системы не равны0(a_ii≠ 0,i= 1, 2, …, n).Разрешим первое уравнение системы относительно x₁, второе относительно x₂ и т.д. Получим следующую эквивалентную систему, записанную в скалярном виде:

(5.8)

Теперь, задав нулевое приближение , по рекуррентным соотношениям (5.8) можем выполнять итерационный процесс, а именно:

(5.9)

Аналогично находятся следующие приближения , где в (5.9) вместонеобходимо подставить.

Условие окончания итерационного процесса

(5.10)

Достаточное условие сходимости.

Если выполнено условие диагонального преобладания, т.е. ,

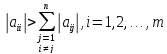
то итерационный процесс сходится при любом выборе начального приближения. Если исходная система уравнений не удовлетворяет условию сходимости, то ее приводят к виду с диагональным преобладанием.

Выбор начального приближения влияет на количество итераций, необходимых для получения приближенного решения. Наиболее часто в качестве начального приближения берут

(5.11)

или .

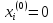4. Метод Гаусса – Зейделя

Расчетные формулы имеют вид:

(5.12)

т.е. для подсчета i–й компоненты (k+1) –го приближения к искомому вектору используется уже вычисленное на этом, т.е. (k+1) – м шаге, новые значения первых i–1 компонент.

Подробные формулы имеют вид:

(5.13)

Достаточное условие сходимости этого метода такое же, как и для метода простой итерации, т.е. диагональное преобладание:

Начальное приближение: .

Задание к лабораторной работе №5

Таблица 4.1 – Исходные данные для выполнения самостоятельного задания

№ В	Система линейных уравнений	№ В	Система линейных уравнений
1		13
2		14
3		15
4		16
5		17
6		18
7		19
8		20
9		21
10		22
11		23
12		24

Решить систему линейных уравнений:

1. Решить СЛАУ матричным методом и сравнить результаты с расчетом в среде Mathcad;

2. Решить СЛАУ методом Гаусса;

3. Решить СЛАУ методом простой итерации;

4. Решить СЛАУ методом Зейделя.

Содержание отчета

Отчет по лабораторной работе должен содержать:

1. Титульный лист, оформленный согласно приложению 1;

2. Условие задания и порядок выполнения расчетов.

3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;

4. Выводы о проделанной работе.

Контрольные вопросы

1. Объяснить суть метода решения СЛАУ метод Крамера;

2. Объяснить суть метода решения СЛАУ методом Гаусса;

3. Объяснить суть метода простой итерации. Условия сходимости метода;

4. Объяснить суть метода Зейделя. Условия сходимости метода.

Лабораторная работа №6

ТОПОЛОГИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

Целью работы является исследование установившихся рабочих режимов сложных схем замещения электрических цепей на базе применения аппарата матриц и элементов топологической теории графов.

Содержание работы

1. Исследование установившегося режима цепи методом контурных токов;

2. Исследование установившегося режима цепи методом узловых напряжений.

Перечень необходимых материалов, приборов, оборудования

Лабораторная работа проводится в компьютерном классе с сетевым оборудованием со следующим программным обеспечением: ОС MS Windows XP и выше, офисный пакет OpenOffice, система инженерных и математических расчетов MathCad.

Методические указания

Режим любой электрической цепи, например изображенной на рис.6.1, однозначно определяется законами Кирхгофа. Вид уравнений электрического состояния цепи, зависит только от схемы соединения ветвей, т.е. от топологической структуры цепи, и не зависит от вида параметров самих элементов. В таком случае, ветви, содержащие различные двухполюсные элементы, можно представлять просто линиями, а структуру цепи - совокупностью этих линий, которая называется графом электрической цепи (рис.6.2). Отрезок линии, соответствующий ветви схемы, называетсяветвью графа. Граничные точки ветви графа называютузлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой.

Рисунок 6.1 Электрическая схема

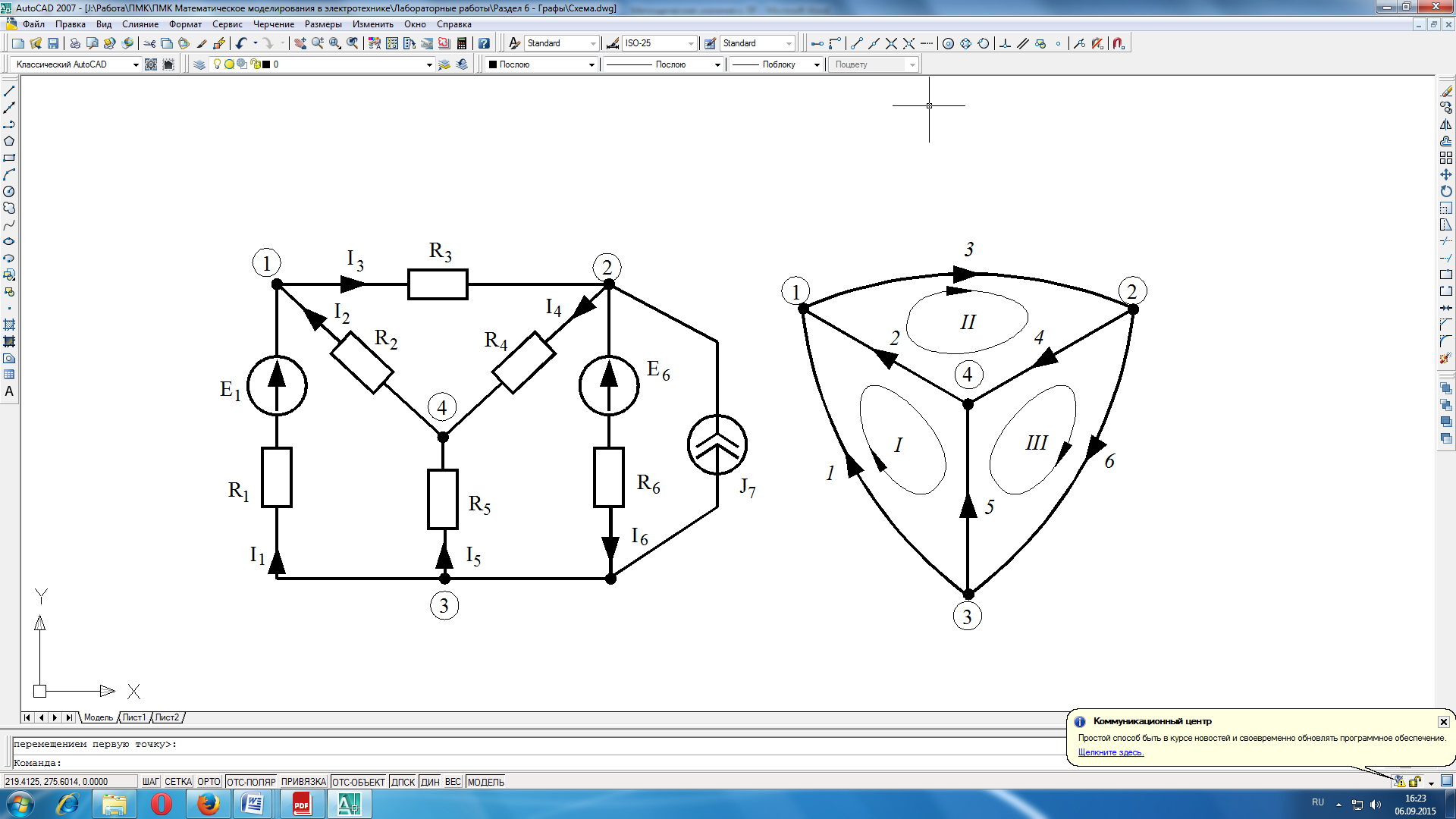
Рисунок 6.2 Граф электрической цепи

Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.

В теории электрических цепей важное значение имеют следующие подграфы:

Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 6.2 ветви 3-6; 2-5; 3-4-5; 1 образуют пути между одной и той же парой узлов 1 и3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.

Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Если между любой парой узлов графа существует связь, то граф называют связным.

Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 6.2 могут служить фигуры на рис. 6.3.

Рисунок 6.3 Примеры деревьев графа

Для аналитического описания структуры электрических цепей применяют топологические матрицы: соединений(узловая) [A] иконтуров[В].

Матрица соединений, ее размерность: число строк = число узлов - 1; число столбцов = число ветвей. Матрица состоит из элементов: 1, -1, 0. Если ток ветви подходит к данному узлу то 1, если отходит то -1, если ветви нет то 0.

Матрица главных контуров, ее размерность: число строк = число контуров - 1; число столбцов = число ветвей. Каждая ветвь должна входить только в один контур. Если ветвь входит в контур и ее направление совпадает с обходом контура то 1, не совпадает -1, ветви нет в контуре 0.

Отметим, что для матриц А, В, составленных для одного и того же графа, должно выполнятся соотношение

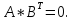(6.1)

Матрицы исходных данных и исходных токов

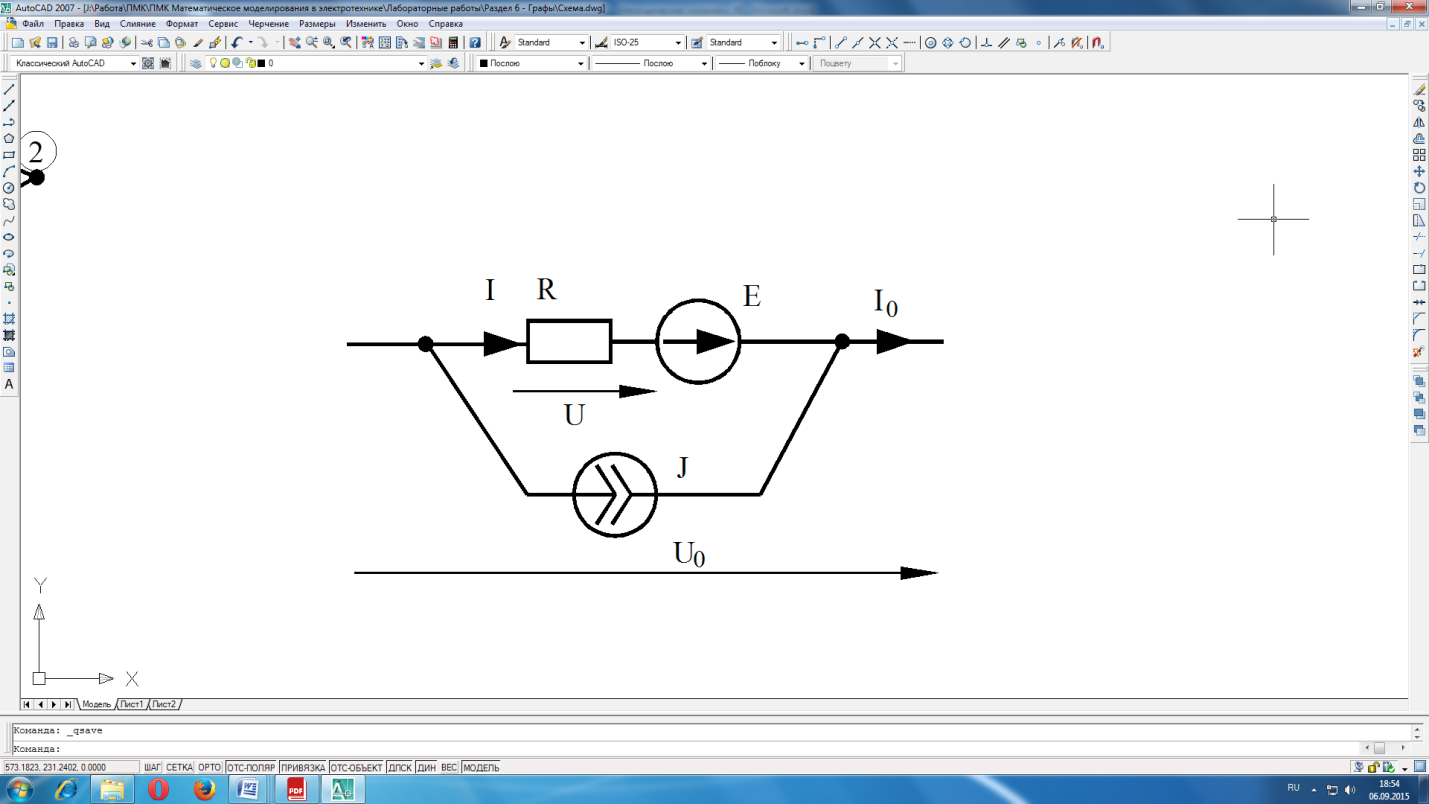
Рисунок 6.4 Обобщенная ветвь с источниками ЭДС и тока

(6.2)

Размерности матриц источников тока, ЭДС, сопротивлений и искомых токов определяются количеством ветвей

; ;

[вх1] [вх1] [вхв] [вх1]