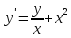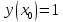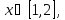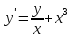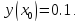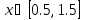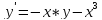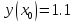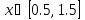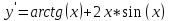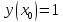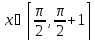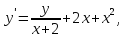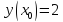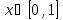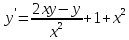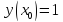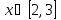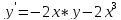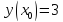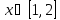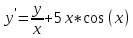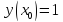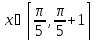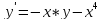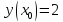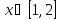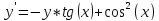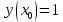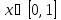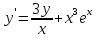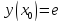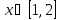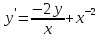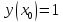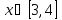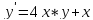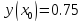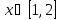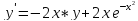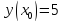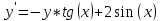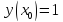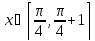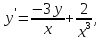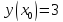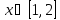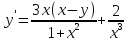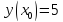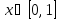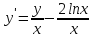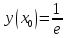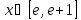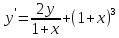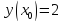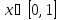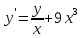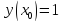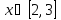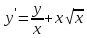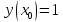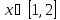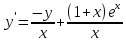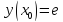- •Лабораторная работа №3 численное интегрирование в задачах электротехники
- •Содержание работы
- •Методические указания
- •1.Метод прямоугольников
- •2. Метод трапеций
- •3. Метод парабол (Симпсона)
- •4. Погрешности расчетов
- •Лабораторная работа №4 численное дифференцирование в задачах электротехники
- •Методические указания
- •1. Метод Эйлера
- •2. Усовершенствованный метод Эйлера
- •3. Модифицированный метод (Эйлера-Коши)
- •4. Метод Рунге-Кутты
- •Лабораторная работа №5
- •2. Метод Гаусса
- •3. Метод простой итерации (метод Якоби)
- •4. Метод Гаусса – Зейделя
- •Лабораторная работа №6
- •Закон Ома в матричной форме
- •Первый закон Кирхгофа в матричной форме
- •Второй закон Кирхгофа в матричной форме
- •Метод контурных токов
- •Метод узловых потенциалов
- •Задание к лабораторной работе №6
- •Лабораторная работа №7 анализ переходных процессов в электрических цепях с использованием Mathcad
- •Содержание работы
- •Методические указания
- •Пример:
- •Контрольные вопросы
- •350072, Краснодар, Московская, 2а
- •350072, Г. Краснодар, ул. Московская, 2, корп. «в», оф. В-120
2. Усовершенствованный метод Эйлера
Точность метода Эйлера можно повысить, если воспользоваться для аппроксимации интеграла более точной формулой интегрирования –формулой трапеций.
Основная идея этого метода: вычисляемое
по формуле (4.5) очередное значение
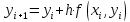 будет точнее, если значение производной,
то есть угловой коэффициент прямой
замещающей интегральную кривую на
отрезке
будет точнее, если значение производной,
то есть угловой коэффициент прямой
замещающей интегральную кривую на
отрезке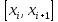 будет вычисляться не по левому краю (то
есть в точке
будет вычисляться не по левому краю (то
есть в точке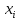 ),
а по центру отрезка
),
а по центру отрезка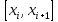 .
Но так как значение производной между
точками
.
Но так как значение производной между
точками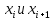 не вычисляется, то перейдем к сдвоенным
участкам
не вычисляется, то перейдем к сдвоенным
участкам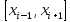 центром, в которых является точка
центром, в которых является точка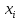 ,
при этом уравнение прямой получает вид:
,
при этом уравнение прямой получает вид:
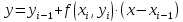 (4.6)
(4.6)
А формула (5) получает вид
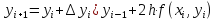 (4.7)
(4.7)
Формула (4.7) применена только для
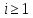 ,
следовательно, значения
,
следовательно, значения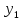 по ней получить нельзя, поэтому
по ней получить нельзя, поэтому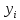 находят по методу Эйлера, при этом для
получения более точного результата
поступают так: с начала по формуле (4.5)
находят значение
находят по методу Эйлера, при этом для
получения более точного результата
поступают так: с начала по формуле (4.5)
находят значение
 (4.8)
(4.8)
В точке
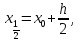 а затем находится
а затем находится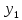 по
формуле (4.7) с шагом
по
формуле (4.7) с шагом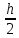
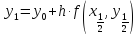 (4.9)
(4.9)
После того как
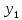 найдено дальнейшие вычисления при
найдено дальнейшие вычисления при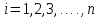 производится по формуле (4.7)
производится по формуле (4.7)
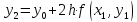 ….
….
3. Модифицированный метод (Эйлера-Коши)
Повысить точность и устойчивость вычисления решения можно с помощью неявного метода Эйлера следующего вида.
Прогноз:
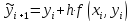 (4.10)
(4.10)
Коррекция:
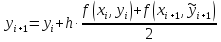 (4.11)
(4.11)
Геометрически это означает, что с начало
определяется направление интегральной
кривой в исходной точке
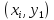 и во вспомогательной точке
и во вспомогательной точке ,
а в качестве окончательного направления
берется среднее значение этих направлений.
,
а в качестве окончательного направления
берется среднее значение этих направлений.
Благодаря более точной формуле интегрирования, погрешность метода пропорциональна уже квадрату шага интегрирования.
4. Метод Рунге-Кутты
Воспользовавшись хорошо зарекомендовавшей себя формулой Симпсона, можно получить еще более точную формулу для решения задачи Коши для ОДУ первого порядка - широко используемого в вычислительной практике метода Рунге-Кутты.
В формуле Симпсонадля приближенного вычисления определенного интеграла используются значения подинтегрального выражения в трех точках. В интеграле их всего две, поэтому введем дополнительную точку в середине отрезка [xi+1 , xi].
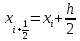
тогда можно определить так
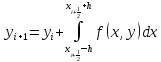
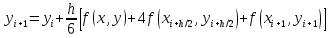
Полученное выражение является неявным,
так как в правой части содержатся
еще не определенные значения
функции yi+h/2 и yi+1.
Чтобы воспользоваться этой формулой,
надо использовать некоторое приближение
для вычисления этих значений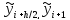 .
.
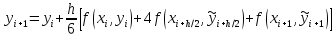
При использовании различных методов приближенного вычисления этих величин, получаются выражения для методов Рунге-Кутты различного порядка точности.
Алгоритм Рунге-Кутты четвертого порядка - (погрешность порядка h4):
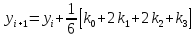
где

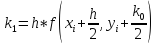

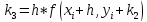
Алгоритм четвертого порядка требует на каждом шаге четырех вычислений функции соответственно, но является весьма точным.
Задание к лабораторной работе №4
Таблица 4.1 – Исходные данные для выполнения самостоятельного задания
|
№ варианта |
Функции |
Начальные условия |
Интервал |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
Вариант выполнения работы соответствует порядковому номеру в журнале проведения занятий преподавателя. Данные выбираются из табл.4.1.
Для заданной функции y = f(x) выполнить следующее:
1. Подобрать оптимальный шаг интегрирования дифференциального уравнение методом Эйлера при котором относительное изменение решения составит 5%. Первоначальный шаг hвыбрать равным 1/10 интервала интегрирования. Последующие шаги уменьшать в 2 раза. Используя программу расчета в средеMathcadпроверить результаты.
2. Решить дифференциальное уравнение усовершенствованный методом Эйлера взяв шаг интегрирования из пункта 1. Проверить результаты используя Mathcad.
3. Решить дифференциальное уравнение модифицированным методом Эйлера-Коши взяв шаг интегрирования из пункта 1. Проверить результаты используя Mathcad.
4. Решить дифференциальное уравнение методом Рунге-Кутты взяв шаг интегрирования из пункта 1. Проверить результаты используя Mathcad.
5. Сравнить точность расчетов приведенных методом.
Содержание отчета
Отчет по лабораторной работе должен содержать:
1. Титульный лист, оформленный согласно приложению 1;
2. Условие задания и порядок выполнения расчетов.
3. Протокол работы в виде документа Mathcad с текстовыми блоками заголовков заданий и формульных блоков их выполнения по каждому пункту заданию согласно своему варианту;
4. Выводы о проделанной работе.
Контрольные вопросы
1. Объяснить суть решения дифференциального уравнения методом Эйлера.
2. Объяснить суть решения дифференциального уравнения усовершенствованный методом Эйлера .
3. Объяснить суть решения дифференциального уравнения модифицированным методом Эйлера-Коши.
4. Объяснить суть решения дифференциального уравнения методом Рунге-Кутты .