31.Характеристические функции. Понятие о центральной предельной теореме.

До сих пор мы задавали случайные величины законом распределения. Характеристическая функция - ещё один способ представления случайных величин.

Пусть X - случайная величина. Её характеристической функцией w(t) назовём математическое ожидание случайной величины e^itX:

w(t)=Me^itX,

где под комплексной случайной величиной e^itX мы понимаем комплексное число e^{it X}=cos(tX)+isin(tX), а

;

независимая переменная t имеет размерность X^-1.

Характеристическая функция - преобразование Фурье-Стилтьеса функции распределения:

.

В непрерывном случае w(t) - преобразование Фурье плотности вероятности:

Если w(t) абсолютно интегрируема, то обратное преобразование Фурье позволяет восстановить плотность f(x) по характеристической функции:

.

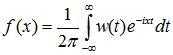В дискретном случае:

.

Особо отметим дискретные случайные величины с целочисленными значениями, например, при x_k=k:

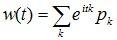
здесь w(t) - ряд Фурье в комплексной форме, вероятности p_k играют роль коэффициентов Фурье и легко восстанавливаются по w(t):

.

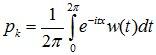В общем случае восстановление закона распределения по характеристической функции тоже возможно, но более сложно.

 

Свойства характеристических функций

Важнейшим свойством характеристической функции, сделавшим её одним из главных инструментов современной теории вероятностей, оказалось то, что при суммировании независимых случайных величин их характеристические функции перемножаются: если X и Y независимы, то для случайной величины Z=X+Y:w_Z(t)=w_X(t)×w_Y(t).

Действительно,

w_Z(t)=M(e^itZ)=M(e^it(X+Y))=M(e^itX×e^itY)=M(e^itX)×M(e^itY)=w_X(t)×w_Y(t).

Законы распределения при суммировании независимых слагаемых ведут себя гораздо сложнее (см. Л12, закон распределения суммы случайных величин).

Если Y=aX+b, то

w_Y(t)=M(e^it(aX+b))=e^itb×M(e^itaX)=e^itb×w_X(at).

Другим важным свойством характеристических функций является их простая связь с моментами.

Предполагая возможность дифференцирования под знаком математического ожидания в равенстве w(t)=Me^itX, получим:

w^(k)(t)=i^kM(X^k×e^itX).

При t=0:

Таким образом, характеристическая функция позволяет заменить интегрирование при вычислении моментов дифференцированием.

В частности,

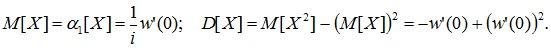
Характеристическую функцию определяют также и для n-мерной случайной величины (X₁, X₂, , ¼ , X_n):

w(t₁, t₂, , ¼ , t_n)=M(expi(t₁X₁+t₂X₂+¼+t_nX_n)).

Центральная предельная теорема.

Первый вариант этой теоремы был доказан в 1912 г. А.М.Ляпуновым. В настоящее время имеется несколько формулировок этой теоремы, различающихся условиями, которые накладываются на случайные величины. Мы приведём простейший вариант центральной предельной теоремы для одинаково распределённых независимых случайных величин.

Пусть последовательность одинаково распре­делённых случайных величин с математическими ожиданиямии дисперсиями.

ТЕОРЕМА. Если случайные величины независимы и, то при достаточно большомn закон распределения суммы будет сколь угодно близок к нормальному закону распределения.

Так как в условиях теоремы случайные величины независимы, то

т.е. в условиях теоремы сумма имеет закон распределения близкий к.Так' какna и  с ростом п, возрастают, то удобнее рассматривать не просто суммы , а нормированные суммы. Такие суммы приимеют закон распределения.

Мы не приводим доказательства теоремы потому, что оно требует введения многих дополнительных понятий и утверждений. Было потрачено немало усилий, чтобы ослабить условия, налагаемые на случайные величины в центральной предельной теореме. В частности, оказалось, что утверждение теоремы остаётся в силе и для слабо зави­симых случайных величин. Как уже отмечалось, существует много вариантов и соответственно формулировок центральной предельной теоремы, но во всех этих вариантах суть условий одна: Если случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зави­симых) случайных величин, каждая из которых мала по сравнению с суммой, то эта сумма имеет закон распределения близкий к нормальному.

Пример 1. Наглядной иллюстрацией действия центральной предельной теоремы является рассеивание снарядов при артиллерийской стрельбе. На траекторию снаряда действует большое количество независимых факторов, влияние каждого из которых невелико. Этими факторами являются отклонения в размере заряда, в размере и весе снаряда, сила и направле­ние ветра на разных высотах, плотность воздушных вихрей, зависящая от температуры и влажности воздуха, и т.д.

В результате отклонение снаряда от цели имеет приблизительно нормальный закон распределения.

Пример 2. Другими широко известным примером может служить ошибка возникшая при измерениях. Ошибка, как правило, является суммой малых ошибок возникающих из-за действия случайных факторов таких, как температура окружающей среды, состояние наблюдателя, состояние измерительного прибора и т.д.

32.Цепи Маркова.Понятие о случайных процессах.

Цепью Маркова называют такую последовательность случайных событий, в которой вероятность каждого события зависит только от состояния, в котором процесс находится в текущий момент и не зависит от более ранних состояний. Конечная дискретная цепь определяется:

1. множеством состояний S = {s₁, …, s_n}, событием является переход из одного состояния в другое в результате случайного испытания

2. вектором начальных вероятностей (начальным распределением) p⁽⁰⁾ = {p⁽⁰⁾(1),…, p⁽⁰⁾(n)}, определяющим вероятности p⁽⁰⁾(i) того, что в начальный момент времени t = 0 процесс находился в состоянии s_i

3. матрицей переходных вероятностей P = {p_ij}, характеризующей вероятность перехода процесса с текущим состоянием s_i в следующее состояние s_j, при этом сумма вероятностей переходов из одного состояния равна 1:

∑_j=1…n  p_ij = 1

Пример матрицы переходных вероятностей с множеством состояний S = {S₁, …, S₅}, вектором начальных вероятностей p⁽⁰⁾ = {1, 0, 0, 0, 0}:

С помощью вектора начальных вероятностей и матрицы переходов можно вычислить стохастический вектор p⁽ⁿ⁾ — вектор, составленный из вероятностей p⁽ⁿ⁾(i) того, что процесс окажется в состоянии i в момент времени n. Получить p⁽ⁿ⁾ можно с помощью формулы:

p⁽ⁿ⁾ = p⁽⁰⁾×P ⁿ

Векторы p⁽ⁿ⁾ при росте n в некоторых случаях стабилизируются — сходятся к некоторому вероятностному вектору ρ, который можно назвать стационарным распределением цепи. Стационарность проявляется в том, что взяв p⁽⁰⁾ = ρ, мы получим p⁽ⁿ⁾ = ρ для любого n. Простейший критерий, который гарантирует сходимость к стационарному распределению, выглядит следующим образом: если все элементы матрицы переходных вероятностей Pположительны, то при n, стремящемуся к бесконечности, вектор p⁽ⁿ⁾ стремится к вектору ρ, являющемуся единственным решением системы вида  p × P = p. Также можно показать, что если при каком-нибудь положительном значении n все элементы матрицы P ⁿ положительны, тогда вектор p⁽ⁿ⁾ все-равно будет стабилизироваться. Доказательство этих утверждений есть в [1] в подробном виде.

Марковская цепь изображается в виде графа переходов, вершины которого соответствуют состояниям цепи, а дуги — переходам между ними. Вес дуги (i, j), связывающей вершины s_i и s_jбудет равен вероятности p_i(j) перехода из первого состояния во второе. Граф, соответствующий матрице, изображенной выше:

Классификация состояний марковских цепей

При рассмотрении цепей Маркова нас может интересовать поведение системы на коротком отрезке времени. В таком случае абсолютные вероятности вычисляются с помощью формул из предыдущего раздела. Однако более важно изучить поведение системы на большом интервале времени, когда число переходов стремится к бесконечности. Далее вводятся определения состояний марковских цепей, которые необходимы для изучения поведения системы в долгосрочной перспективе. Марковские цепи классифицируются в зависимости от возможности перехода из одних состояний в другие.  Группы состояний марковской цепи (подмножества вершин графа переходов), которым соответствуют тупиковые вершины диаграммы порядка графа переходов, называютсяэргодическими классами цепи. Если рассмотреть граф, изображенный выше, то видно, что в нем 1 эргодический класс M₁ = {S₅}, достижимый из компоненты сильной связности, соответствующей подмножеству вершин M₂ = {S₁, S₂, S₃, S₄}. Состояния, которые находятся в эргодических классах, называются существенными, а остальные — несущественными(хотя такие названия плохо согласуются со здравым смыслом). Поглощающее состояние s_i является частным случаем эргодического класса. Тогда попав в такое состояние, процесс прекратится. Для S_i будет верно p_ii = 1, т.е. в графе переходов из него будет исходить только одно ребро — петля.

Поглощающие марковские цепи используются в качестве временных моделей программ и вычислительных процессов. При моделировании программы состояния цепи отождествляются с блоками программы, а матрица переходных вероятностей определяет порядок переходов между блоками, зависящий от структуры программы и распределения исходных данных, значения которых влияют на развитие вычислительного процесса. В результате представления программы поглощающей цепью удается вычислить число обращений к блокам программы и время выполнения программы, оцениваемое средними значениями, дисперсиями и при необходимости — распределениями. Используя в дальнейшем эту статистику, можно оптимизировать код программы — применять низкоуровневые методы для ускорения критических частей программы. Подобный метод называется профилированием кода.

Например, в алгоритме Дейкстры присутствуют следующие состояния цепи:

• vertex (v), извлечение новой вершины из очереди с приоритетами, переход только в состояние b;

• begin (b), начало цикла перебора исходящих дуг для процедуры ослабления;

• analysis (a), анализ следующей дуги, возможен переход к a, d, или e;

• decrease (d), уменьшение оценки для некоторой вершины графа, переход к a;

• end (e), завершение работы цикла, переход к следующей вершине.

Остается задать вероятности переходом между вершинами, и можно изучать продолжительности переходов между вершинами, вероятности попадания в различные состояния и другие средние характеристики процесса.

Аналогично, вычислительный процесс, который сводится к обращениям за ресурсами системы в порядке, определяемом программой, можно представить поглощающей марковской цепью, состояния которой соответствуют использованию ресурсов системы – процессора, памяти и периферийных устройств, переходные вероятности отображают порядок обращения к различным ресурсам. Благодаря этому вычислительный процесс представляется в форме, удобной для анализа его характеристик.

Цепь Маркова называется неприводимой, если любое состояние S_j может быть достигнуто из любого другого состояния S_i за конечное число переходов. В этом случае все состояния цепи называются сообщающимися, а граф переходов является компонентой сильной связности. Процесс, порождаемый эргодической цепью, начавшись в некотором состоянии, никогда не завершается, а последовательно переходит из одного состояния в другое, попадая в различные состояния с разной частотой, зависящей от переходных вероятностей. Поэтому основная характеристика эргодической цепи –  вероятности пребывания процесса в состояниях S_j, j = 1,…, n, доля времени, которую процесс проводит в каждом из состояний. Неприводимые цепи используются в качестве моделей надежности систем. Действительно, при отказе ресурса, который процесс использует очень часто, работоспособность всей системы окажется под угрозой. В таком случае дублирование такого критического ресурса может помочь избежать отказов. При этом состояния системы, различающиеся составом исправного и отказавшего оборудования, трактуются как состояния цепи, переходы между которыми связаны с отказами и восстановлением устройств и изменением связей между ними, проводимой для сохранения работоспособности системы. Оценки характеристик неприводимой цепи дают представление о надежности поведения системы в целом. Также такие цепи могут быть моделями взаимодействия устройств с задачами, поступающими на обработку.

Случайный процесс описывается статистическими характеристиками, называемыми моментами. Кроме того, важнейшими характеристиками случайного процесса являются его стационарность и эргодичность, а также спектр мощности.