
Основы теории систем и вычислительные схемы системного анализа
.pdf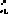
Если потребовать, чтобы эта функция совпадала со статистическими данными, то можно подобрать множество таких функций. Т.о. при восстановлении функции, необходимо
-выбрать класс аппроксимирующих функций,
-точность аппроксимации,
-критерий согласия между функцией и статистическими данными.
Обычно на практике используют следующие классы функций: 1)линейные комбинации функций 1, x, x2, ... , xn , т.е. функции из класса
полиномов степени не выше n (аппроксимация алгебраическим многочленом заданной степени);
2)линейные комбинации функций Sin(akx) и Cos(akx) (аппроксимация тригонометрическим многочленом, или отрезком ряда Фурье);
3)комбинации экспоненциальных функций Exp( 

 kx) c вышеуказанными и некоторые другие;
kx) c вышеуказанными и некоторые другие;
4) классы функций, удовлетворяющие ранее заданным свойствам (производственные функции, функция затрат и т.д.)
В качестве критерия согласия используют три условия:
1)точное совпадение значений искомой функции со статистическими данными (критерий интерполяции);
2)сумма квадратов отклонений значений искомой функции и заданных значений должна быть минимальной (критерий среднеквадратической аппроксимации);
3)максимальное по абсолютной величине из отклонений значений искомой функции заданных значений должно быть минимальным (критерий равномерной аппроксимации).
Если же об аналитическом виде функции ничего неизвестно, то, полагая, что она является непрерывной функцией, вид ее можно найти, используя теорему Колмогорова.
Теорема Колмогорова. Любая непрерывная функция от n переменных F(x1 ,x2 ,...,xn ) может быть представлена в виде суперпозиции 3n +1 функции
F (x1, x2 ,..., xn )= 2∑n +1 g j ∑n |
hij (xi ) |
, |
||
где g j (•) |
j =1 |
i =1 |
|
|
и hij (•) |
- непрерывные функции, не зависящие от вида |
|||
представляемой функции F.
При всей своей математической красоте теорема Колмогорова малоприменима на практике. Это связано с тем, что функции hij — негладкие и трудно вычислимые; также неясно, каким образом можно подбирать функции gj для данной функции F. Роль этой теоремы состоит в том, что она показала принципиальную возможность реализации сколь угодно сложных зависимостей с помощью относительно простых автоматов, например, нейронных сетей.
Т.о., если система описана как черный ящик, и необходимо знать аналитический вид передаточной функции системы, то его можно
21
восстановить по статистике функционирования системы. Другим способом является структурирование системы, т.е. введение элементов и связей между ними.
Целевые структурированные системы описываются следующим образом
Stст =< Sисх;(t0 ,t,T );( X t ,GX );(Yt ,GY );Yt = F( X t ); Zt = H (Zt −1, X t );Фц( X t , Z0 ) >
Фц(•) - функция цели.
Цель системы может быть задана не функциональной зависимостью, а конечным целевым состоянием системы. Пусть St0 - система в начальный
момент времени, ST - характеристики конечной системы, целевое состояние системы.
Путь, по которому развивается система в период времени [t0 ,T ],
называется траекторией системы {Yt }Tt0 .
Задача исследования целевой структурированной системы состоит в поиске такой траектории, благодаря которой будут использованы имеющиеся ресурсы и достигнуто максимальное значение выбранной цели.
Каждой целевой системе можно поставить в соответствие модель:
T |
|
|
|
|
( max minФ(Z0 , X t ) ) |
∑Ф(Z0 , X1t ,.., X nt ) → max |
|||||
t =1 |
|
|
t |
Xt t |
|
X t GX |
|
||||
Yt GY |
|
t |
|
||
Zt = H (Zt −1, X t ) t |
|
||||
Пример 1. |
m |
|
отраслей (i =1,..,m ), производящих продукт в период |
||
Пусть имеется |
|
||||
времени [t0 ,T ], |
объем выпуска отраслей в каждый момент времени задается |
||||
производственной функцией, например, функцией Кобба-Дугласа |
|||||
|
y |
it |
= a |
Kα L1−αeγt |
(1) |
|
|
t |
it it |
|
|
22
где K - капитал, L - труд.
Вкаждый момент времени распределяются дополнительные
финансовые ресурсы Bt (их величина задана), βit - доля, идущая в году t на капитал; μit - доля финансовых ресурсов, идущая в году t на труд.
Формирование капитала и труда в момент времени t описываются уравнениями
Kit = Kit −1 + βit |
Bt |
i,t (2) |
||
Lit = Lit −1 + μit |
Bt |
i,t (3) |
||
0 ≤ βit ≤1 |
,0 ≤ μit |
≤1 i,t |
(4) |
|
m |
m |
|
|
|
∑βit =1, |
∑μit =1 |
t |
(5) |
|
i=1 |
i=1 |
|
|
|
Ограничение на дополнительный финансовый ресурс
Kit0 = K0 , Lit0 = L0 |
i (6) |
t = t0 ,..,T |
(7) |
Функция цели – максимизация суммарного выпуска всех отраслей за период времени [t0 ,T ]
m
∑ yit → max (8)
i=1
Модель (1)-(8) называется моделью Лисичкина. Данная задача – задача оптимального управления, которая решается составлением аналога функции Лейбница – Гамильтониана. Необходимо найти оптимальное управление, т.е. такое значение переменных βit , μit , на которых Гамильтониан достигает
своего максимума.
Пример 2. Самолет находится на высоте H0 и летит со скоростью v0 , необходимо рассчитать программу подъема самолета на высоту HT и развитие скорости vT с минимальной затратой горючего, если задана норма
расхода горючего при изменении высоты и неизменной скорости и изменении скорости при постоянной высоте.
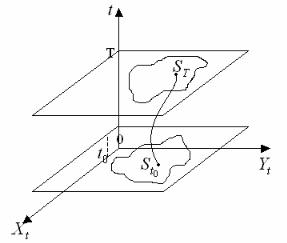
Для решения задачи введем сетку изменения расстояния и скорости –
разобьем |
интервал |
изменения скоростей |
[v0 , vT ] на |
5 равных частей, а |
интервал |
высот на |
4. Затраты топлива |
d заданы |
и записаны у ребер |
полученного графа.
23
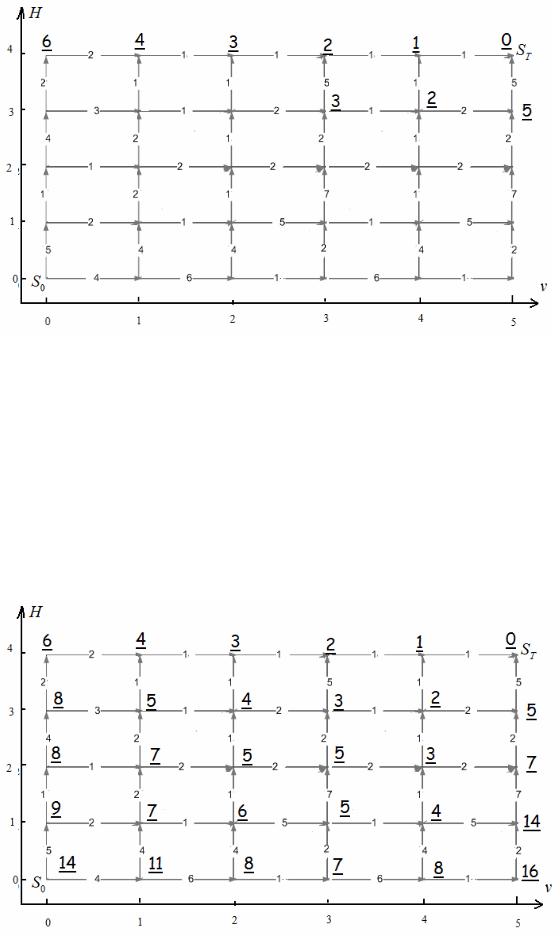
Текущее состояние характеризуется парой (vt , Ht ) , а также минимальными затратами топлива St , необходимыми для перевода самолета из текущего в
конечное состояние, управляющее воздействие заключается в выборе состояния, в которое необходимо перевести самолет в следующий момент времени. Будем решать задачу методом динамического программирования – оптимизировать переход в новое состояние, начиная с последнего. Очевидно,
что ST = S(5,4) = 0 , S(4,4) = S(5,4) +1 = 0 +1 =1, |
S(3,4) = S(4,4) +1 = 2, |
…, S(5,3) = S(5,4) +5 = 5, |
|
S(4,3) = min(S(5,3) + 2, S(4,4) +1) = min(7,2) = 2, |
т.е. чтобы попасть из |
состояния (4,3) в конечное состояние (5,4) необходимо 2 ед. топлива. Далее
S(3,3) = min(S(3,4) +5, S(4,3) +1) = min(7,3) = 3 .
24
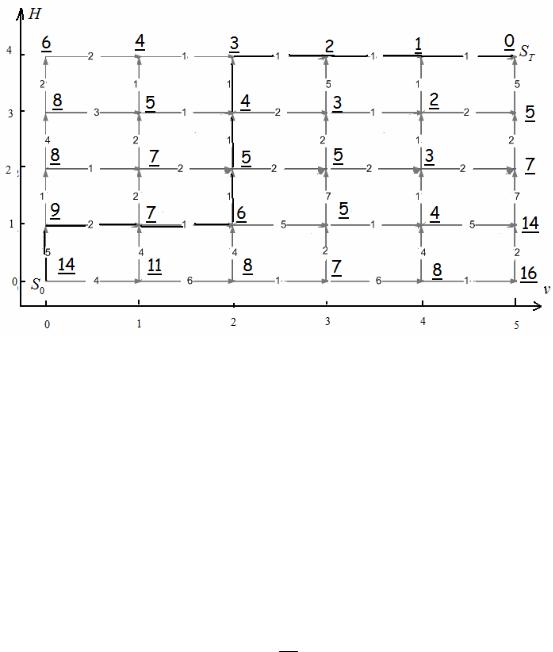
Т.о. получаем S(0,0) =14 – минимальные затраты топлива для перехода из S0 в ST . Найдем теперь режим перевода системы (самолета) в конченое состояние. S(0,0) =14, очевидно, что следующим должен быть переход в состояние (0,1), т.к. S(0,1) +5 =14 = S(0,0) . Далее возможен любой переход,
т.к. затраты топлива одинаковы и для перехода в (0,2) и в состояние (1,1) : S(0,1) = 9 = S(0,2) +1 = S(1,1) + 2 . Выберем, например, переход в (1,1). Т.о.
получаем следующий режим перевода системы в конечное состояние: (0,0)-(0,1)-(1,1)-(2,1)-(2,2)-(2,3)-(2,4)-(3,4)-(4,4)-(5,4).
Пример 2. Проведено 15 экспериментов по измерению значений |
yi функции |
||||||||||||||
F в точках xi , получена статистика |
|
|
|
|
|
|
|
|
|
||||||
xi |
-8 |
-7 |
-6 |
-5 |
-3 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
11 |
12 |
yi |
-16 |
-14 |
-11 |
-10 |
-6,5 |
3 |
4 |
6 |
8 |
11 |
12,5 |
14 |
18 |
23 |
24 |
Известно, что искомая функция принадлежит семейству функций
F(x)= A·x + B/x. Найти параметры A, B функции, измерения которой были получены.
Будем решать данную задачу методом наименьших квадратов. Подберем параметры A и B так, чтобы обеспечить минимум суммы квадратов отклонений между экспериментальными значениями Yi и ожидаемыми (расчётными) значениями Yi =F(Xi):
T (A, B) = 1 ∑N [F(Xi ) −Yi ]2
N i=1
В нашем случае так называемая остаточная дисперсия определяется выражением
T (A, B) = |
1 ∑[Axi + B 1 |
− yi ]2 → min |
(1) |
||
|
|
N |
|
|
|
|
N |
i=1 |
xi |
A,B |
|
|
|
|
|
|
|
25
Дифференцируя (1) по A и B, получаем систему уравнений
∂T |
|
|
|
|
|
1 |
|
N |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
= 2 |
|
|
|
|
∑[Axi + B |
|
|
|
− yi ] xi |
= 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∂A |
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
N i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
|
|
|
|||||||||
|
∂T = 2 |
|
|
1 ∑[Axi + B 1 − yi ] 1 = 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂B |
|
|
|
|
|
|
|
N i=1 |
|
|
|
|
|
xi |
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
N |
|
|
2 |
|
|
|
|
1 |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
∑xi |
A + B = |
|
|
|
∑ yi xi |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
N i=1 |
|
|
|
|
|
|
|
N i=1 |
|
|
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
N |
1 |
|
1 |
|
|
N |
|
yi |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
A + |
|
|
|
∑ |
B = |
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
N i=1 xi |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
N i=1 xi |
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
N |
|
N |
|
|||||
Введем следующие обозначения S1 = |
∑xi2 , S2 |
= |
∑ yi xi , S3 |
= |
∑ |
, |
|||||||||||||||||||||||||||||||
|
|
|
x2 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N i=1 |
|
N i=1 |
|
N i=1 |
|
|||||
|
|
|
|
1 |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
||||
|
|
|
|
|
|
N |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
S4 |
= |
|
|
|
|
∑ |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
N i |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда (3) можно записать в виде |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
S A + B = S |
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A + S3 B = S4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Получили линейную систему из 2-х уравнений относительно 2-х неизвестных A и B. Главный определитель системы (4):
D = |
S1 |
1 |
= S S |
3 |
−1 ≠ 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1 |
S3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а вспомогательные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
D |
A |
= |
|
S2 |
1 |
|
= S |
2 |
S |
3 |
− S |
4 |
, |
|
D |
B |
= |
|
S1 |
S2 |
|
= S |
S |
4 |
− S |
2 |
||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
S4 |
S3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
S4 |
|
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Тогда решение системы (4) можно найти по формулам Крамера: |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
A = |
DA |
, B = |
DB |
|
|
|
|
|
|
|
|
|
(5) |
|
|
||||||||||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Качество полученной аппроксимации определяется величиной остаточной дисперсии T(A,B) (чем ближе она к нулю, тем лучше подобранная зависимость аппроксимирует наблюдения). Далее необходимо подставить значения наблюдений в формулу (5) и найти численное значение параметров
A, B .
Задачи
1. Самолет находится на высоте H0 и летит со скоростью v0 , необходимо рассчитать программу подъема самолета на высоту HT и развитие скорости vT с минимальной затратой горючего, если задана норма расхода горючего.
26

а) a = 2,b = 5, c = −5, d = −3 б) a = 5,b =1, c = −5, d = 3 в) a = 3,b = −2, c = 5, d = −3
2.Найдите численное решение задачи из примера 2 п.1.3.
3.Проведено 15 экспериментов по отысканию значений линейной функции, получены следующие значения
xi |
-10 |
-8 |
-7 |
-5 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
11 |
12 |
yi |
-6 |
-5 |
-3 |
-2,5 |
-2 |
-1 |
1 |
1 |
2 |
3,5 |
3 |
4,5 |
4 |
5 |
7 |
Восстановите вид функции, используя метод наименьших квадратов.
4. Проведено 15 экспериментов по отысканию значений функции F , получены следующие значения
xi |
-8 |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
yi |
17 |
15 |
13 |
10 |
8,7 |
6,5 |
4,3 |
2 |
-2 |
-4 |
-6 |
-8 |
-11 |
-13 |
-15 |
Какая из функций точнее аппроксимирует функцию F : F1(x)= A·x + B/x или линейная F2(x)= A·x + B.
§2. Основы теории управления. 2.1. Понятие сложности. Сложные системы.
Объект или систему будем называть сложной, если выполнено одно из свойств:
1.элементы системы, которые можно назвать подсистемами или рядовыми элементами, сами являются системами.
2.система является крупномасштабной, состоит из большого числа элементов и разнообразной системы связей между элементами.
Система считается крупномасштабной, если объем информации для описания элементов и связей между ними равен числу БааверманаN =1093 .
27
3.реакция системы на однотипный вход неоднозначна и часто определяется как нечеткая.
При анализе систем используется 3 типа сложности:
1.организованная простота;
2.неорганизованная сложность;
3.организованная сложность.
Кпервому типу задач относятся задачи моделирования сложных процессов на основе выделения основных закономерностей, характеристик и параметров, обеспечивающих достижение цели с минимальными информационными, техническими и материальными средствами. Примерами таких задач являются модель межотраслевого баланса, модель Новожилова, Канторовича, модели смешивания, развития и размещения отраслей.
Кзадачам неорганизованной сложности относятся задачи, которые могут быть решены на основе исследования статистических закономерностей, причем каждый исследуемый элемент рассматривается как статистическая единица, а не как индивидуальный элемент.
Самые сложные задачи – задачи организованной сложности, когда в качестве объекта исследования выступают отдельные единицы и взаимосвязи между ними, причем, чем больше единиц и глубже взаимосвязь, тем система сложнее.
Вкачестве одной из основных характеристик сложности выступает мера
сложности. Пусть задана |
некоторая система X . |
Функция CX : X → R |
|||
является мерой сложности системы X , если выполнены следующие условия: |
|||||
1. |
CX ( ) = 0 . |
|
|
|
|
2. |
Если X A подсистема X B ( X A X B ), то CX A ≤ CX B . |
|
|||
3. |
Если X A ∩ X B = , то |
CX A X B |
= CX A +CX B . |
CX A = CX B , если |
X A |
Меры сложности изоморфных систем равны: |
|||||
изоморфна X B . Если X A |
и X B |
гомоморфные системы ( X A X B ), |
то |
||
CX A |
≤ CX B . |
|
|
|
|
Построение меры сложности любой системы включает в себя следующие этапы:
1.расчет числа элементов системы;
2.определение набора характеристик каждого элемента, необходимых для описания системы;
3.определение возможного числа состояний каждой характеристики;
4.расчет общее число единиц необходимое для описания системы;
5.выбор функции, удовлетворяющей требованиям меры, с помощью которой можно рассчитать сложность системы.
2.2.Управление сложными системами. Типы управления
Управление – совокупность действий, направленных от субъекта управления
кобъекту (ОУ) и обеспечивающих движение системы от некоторого
начального состояния t0 к конечному T , при котором достигается цель.
28
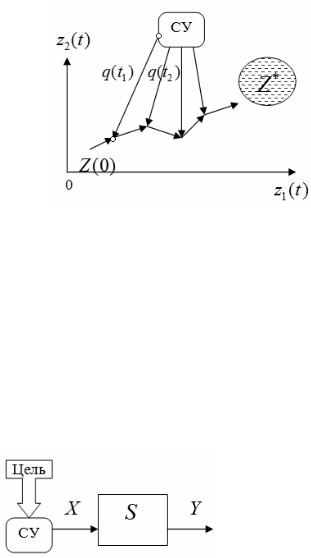
Задача субъекта управления (СУ) состоит в выработке управляющих воздействий, приводящих ОУ к цели.
Пусть ОУ является некоторая система, Z(t) = (z1(t), z2 (t)) - вектор
характеристик ее состояний в момент времени t , Z* - область состояний, характеризующая цель системы. Тогда процесс управления состоит в выработке последовательности управляющих воздействий
q(t1 ), q(t2 ),.., q(tm ) , приводящих систему к целевой области Z* (см. схему 5).
Схема 5. Управление системой
Классификацию типов управления будем проводить по виду связи между воздействием на систему и ее реакцией на это воздействие, тогда можно выделить три типа управления:
- жесткое управление или управление без обратной связи; -управление с обратной связью; -адаптивное управление.
Жесткое управление характеризуется безукоризненно точным выполнением управляющих воздействий СУ (поток X ), даже если отклонение от предписаний СУ привело бы к более быстрому и/или эффективному достижению цели ОУ.
Схема 6. Жесткое управление
Примером системы с жестким управлением может служить светофор. Состояния, характеризующие данную систему – свет, горящий на светофоре. Управление заключается в переключение света (изменение состояний) и осуществляется такое управление с заданной периодичностью. Причем, даже если состояние светофора – красный свет для пешеходов, а на дороге не наблюдается движения машин, для пешеходов продолжает гореть красный свет.
29
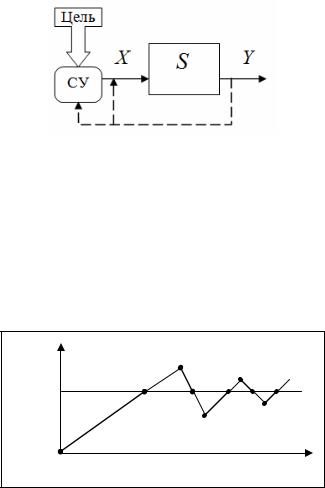
Управление с обратной связью характеризуется изменением набора управляющих воздействий в зависимости от того, как система реагировала на воздействие в предыдущий момент времени.
Схема 7. Управление с обратной связью
Примером системы с обратной связью может служить автопилот самолета, которому задается курс самолета и автопилот корректирует управление при отклонении от заданного курса. На рисунке представлена траектория движения самолета при корректировке автопилотом высоты полета самолета ( H ) в случае отклонения от установленной оптимальной высоты полета
( H * ). Точками на графике обозначены моменты корректирующих воздействий автопилотом.
H |
|
H * |
|
0 |
t |
Адаптивное управление – особый вид управления, характерный для очень сложных систем (биологический организм, государство). Системы адаптивного управления помимо постоянно функционирующей части имеют резервную систему, которая может взять на себя часть или все функции системы управления. Характерной особенностью таких систем является сверхустойчивость – случайные разрушения части системы не выводят из строя всю систему.
30
