7.2 Венгерский метод решения задачи о назначениях

Алгоритм венгерского метода включает в себя 4 этапа.

1. Приведение матрицы.

2. Вычисление максимального числа независимых нулей в приведенной матрице.

3. Получение новых нулей при .

4. Отыскание n независимых нулей при .

Рассмотрим каждый этап подробнее.

Этап 1

Матрица порядканазываетсяприведенной, если все ее элементы неотрицательны и, кроме того, в каждой строке и в каждом столбце имеются нулевые элементы.

Таким образом, приведенная матрица удовлетворяет двум условиям:

1. ;

2. и.

Для приведения матрицы с элементаминужно воспользоваться эквивалентными преобразованиями (4). При этом вначале осуществляется приведение матрицы по строкам (по столбцам), т.е. ищется наименьший элементв каждой строке и осуществляется переход к матрицес элементами. Если матрицаоказывается неприведенной по столбцам (по строкам), то ищется наименьший вариантв каждом столбце и осуществляется переход к матрице, элементы которой вычисляются следующим образом:. Матрицапо построению является приведенной.

Пример 1. Пусть

.

Легко проверить, что

,

,

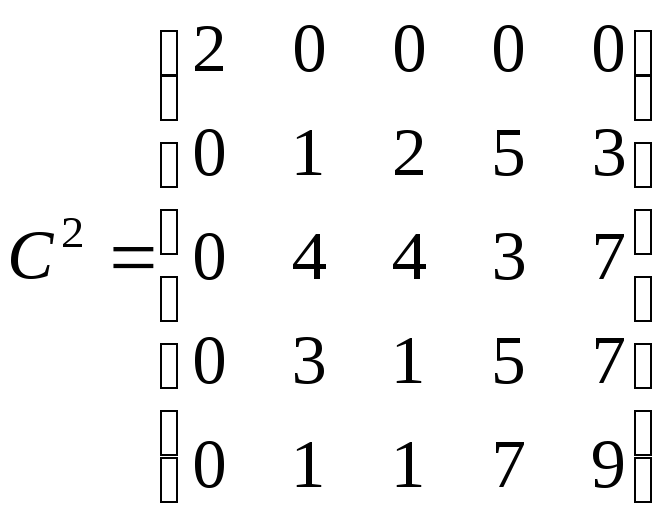причем матрица является приведенной.

Этап 2

При вычислении максимального числа независимых нулей в приведенной матрице обычно организуют полный перебор всевозможных вариантов. При этом необходима воспользоваться следующим утверждением.

Теорема 3. Максимальное число независимых нулей равно минимальному суммарному числу горизонтальных и вертикальных линий (строк и столбцов), которыми можно зачеркнуть все нулевые элементы приведенной матрицы.

Пример 2. Пусть имеется приведенная матрица

из примера 1. Все ее нули содержат 1-ая горизонталь и 1-ая вертикаль, следовательно, здесь .

При решении задачи о назначениях будем проводить указанные линии, в результате чего некоторые элементы окажутся зачеркнутыми, другие — зачеркнуты дважды и остальные — незачеркнутыми.

Этап 3

Обозначим через элемент приведенной матрицы, зачеркнутыйразна 2-м этапе, и положим, где минимум берется по всем, т.е. ищется наименьший из незачеркнутых элементов матрицы. Если теперь провести пересчет элементов матрицыпо формулам

то такие преобразования являются следствием применения Теоремы 1. Пересчитаем элементы матрицы из примера 2 при, в итоге получим приведенную матрицу

.

Все ее нули содержат, например, 1-ая горизонталь и три вертикали: 1-ая, 2-ая, 3-я. Следовательно, здесь и.

Еще один пересчет дает приведенную матрицу

.

Здесь уже

Этап 4

Отыскание независимых нулей осуществляется перебором всех возможных вариантов. Удобно перебор начинать с отыскания строк или столбцов, содержащих единственный нулевой элемент, поскольку такой элемент обязательно войдет в группу независимых. Выбрав элемент, исключают из рассмотрения-ю строку и-й столбец, после чего переходят к отысканию следующего единственного нулевого элемента строки или столбца оставшейся часть матрицы. Действуя подобным образом, можно столкнуться со следующими двумя ситуациями.

1. В результате удается выбрать независимых путей. ОСТАНОВ. Выписать ответ.

2. На некотором шаге все оставшиеся строки и столбцы содержат более одного нулевого элемента. В этом случае выбирается любой нулевой элемент, «помечается» номер строки, из которой выбран 0, и осуществляется переход к выбору следующего нулевого элемента. Если таким образом удается выбрать все независимых нулей, то ОСТАНОВ. Выписать ответ. В противном случае следует возвратиться к помеченной строке и выбрать из нее другой нулевой элемент. По этой схеме надо действовать до тех пор, пока не получимнезависимых нулей.

Пример 4. Взяв матрицу из примера 3, замечаем, что независимыми здесь будут нули с индексами (1,5), (2,2), (3,4), (4,3), (5,1). Это означает, что ответом в задаче о назначениях с матрицейиз примера 1 является матрица назначения вида

,

для которой . Важно отметить, что наряду с указанными здесь будут также независимыми нули с индексами (1,4), (2,5), (3,1), (4,3), (5,2). Следовательно, эта задача о назначениях имеет еще один ответ — матрицу назначений вида

,

причем .

Ответ: при или.