Задания для самостоятельной работы

Задача. На прием к директору записалось несколько человек. Зная время приема каждого и степень важности обсуждаемого вопроса, требуется в таком порядке принимать посетителей, чтобы среднее время проведенное посетителями на приеме было минимально.

Разработать критерий построения оптимального расписания и решить задачу для случая требований. Время обслуживания требованияи степень важностизадать самостоятельно.

6.5 Задача о двух станках

Имеется 2 станка, на которых должны пройти обработку деталей (). Известно время- обработки-й детали на-м станке. Для каждой детали задан свой маршрут обработки на станках.

Требуется составить такое расписание обработки деталей, чтобы длина производственного цикла была минимальной.

Определение. Длиной производственного цикла T назовем время от начала обработки первой детали на первом станке до конца обработки последней детали на последнем станке.

Задача поиска оптимального расписания сводится к определению последовательности , где- перестановка чисел от 1 до, такой, чтобы(длина производственного цикла) было минимальным. Существуетвозможных последовательностей.

Введем следующие обозначения:

- время обработки-й детали на 1-м станке

- время обработки-й детали на 2-м станке

Покажем одну из последовательностей обработки деталей для =5 на диаграмме Ганта (рис. 6.1).

Рисунок 6.1 – Последовательность обработки деталей

Как видно из диаграммы, 2-й станок в любой момент времени или работает или протаивает. Обозначим - время простоя 2-го станка от момента окончания обработкидетали до момента начала обработки-й детали. Общее время работы 2-го станка равно; оно определяется технологией производства а не последовательностью. Очевидно, что

. (6.5)

Требуется минимизировать , но так как- постоянная величина, то задача сводится к минимизации.

Из рис.1 видно, что

если

, если

Выражение для можно переписать в виде

.

Используя те же обозначения, заметим, что

.

Аналогично

,

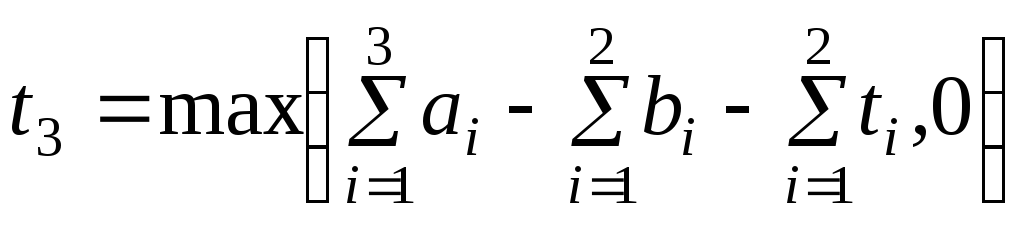Обозначим

,

где есть функция от последовательности. В общем виде

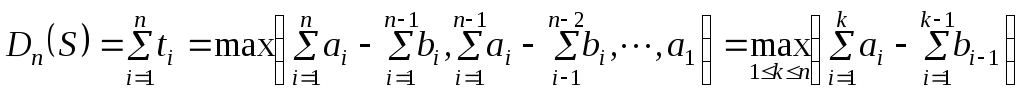(6.6)

Таким образом можно положить

,

откуда

.

Теперь задачу можно сформулировать следующим образом: выбрать такой порядок обработки деталей, чтобы минимизировать .

Пусть теперь имеется порядок :

:

и порядок , полученный изперестановкой-го и ()-го элементов

:.

Значения и, получаемые для порядков следованияи, одинаковы при всех, кроме, быть можети.

Тогда имеем

,

если

.

Если же

,

то какой-то из двух порядков следования ипредпочтительнее. Порядок, в которомследует за, будет лучше, чем, в которомпредшествует, если

. (6.7)

Но

(6.8)

и

. (6.9)

Вычитая из правых частей выражений (6.8) и (6.9), получим следующий результат:

,

или иначе

. (6.10)

Отсюда следует, что порядок предпочтительнее порядка, если.

Рассмотрим тогда порядок

,

которого всегда можно достичь перестановками. Менять местами элементы ине нужно, если

; (6.11)

последнее выполняется, если не превосходит, что можно также записать в виде

.

Следовательно, если в таблице времен можно найти время, не превосходящее всех прочих или, то искомый порядок должен будет начинаться с; если времябудучи по-прежнему наименьшим, равно некоторым другимили, искомый порядок можно будет также начинать с.

Соотношение (6.11) выполняется еще в том случае, когда не превосходит, что можно также записать в виде

.

Следовательно, если в таблице времен можно отыскать время , не превосходящее всех прочихили, то искомый порядок должен завершиться элементом; если время, будучи по-прежнему наименьшим, равно некоторым другимили, искомый порядок можно с таким же правом завершать элементом.