6.3 Целевые функции в задачах теории расписаний

Обычно задача теории расписаний характеризуется целевой функцией (критерием оптимальности), которую необходимо минимизировать (ре­же, максимизировать) на множестве допустимых расписаний. Целевая функция в задачах теории расписаний вычисляется на основе некоторого набора штра­фов (штрафных функций), которые возникают при фиксации порядка обслуживания требований в расписании.

В теории расписаний различают следующие основные типы штрафных функций:

• момент завершения, равный моменту окончания обслужива­ния требования;

• временное смещение;

• запаздывание;

• опережение;

• запаздывание требования.

Можно выделить следующие критерии оптимальности:

• минимаксные критерии - в задачах с такими критериями целе­вая функция представляет собой функцию максимума от значений штрафов требований;

• суммарные критерии - в задачах с такими критериями целевая функция представляет собой сумму значений штрафов требований;

В теории расписаний также исследуются задачи на максимизацию аналогичных целевых функций.

6.4 Построения расписания в случае одного прибора и конечного числа требований

Пусть необходимо обслужить множество требований. Любое требование требует для обслуживанияединиц времени.Требуется составить такое расписание, которое сокращает среднее время пребывания требования в очереди. Критерий такого расписания имеет вид:

, (6.1)

где S – расписание (порядок обслуживания требований),

- время пребывания i-го требования в очереди.

Очевидно, что ,.

Рассмотрим два расписания :

и , полученное изперестановкой-го и-го элементов

.

Распишем критерий оптимальности для этих последовательностей.

, (6.2)

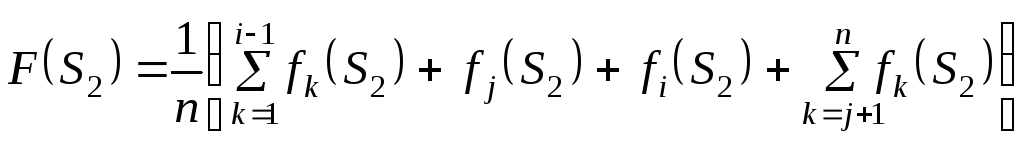. (6.3)

Расписание предпочтительнее расписания , если/

Из принципа построения расписаний и выражений (6.1) и (6.2) видно, что , если выполнено условие

. (6.4)

Рассмотрим отдельно левую и правую части неравенства (6.4).

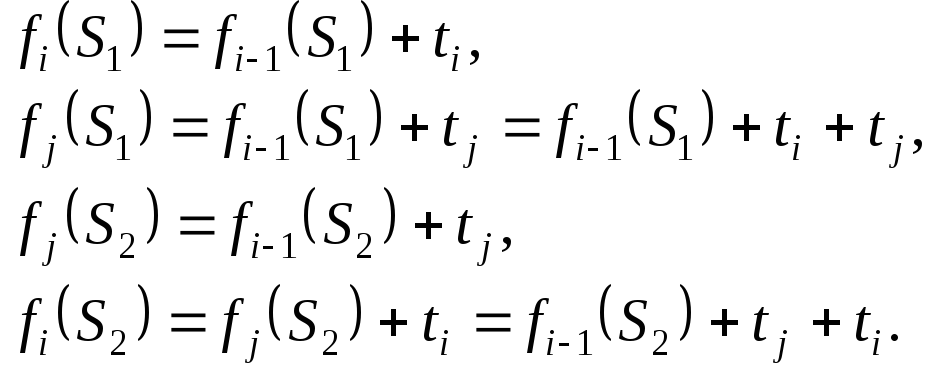
Подставляя полученные выражения в (6.4) и учитывая принцип построения расписаний, получим

.

Образом показано, что , т.е. вперед пропускается требование с наименьшим временем обслуживания.

Для построения оптимального расписания, позволяющего сократить среднее время обслуживания требований с учетом их пребывания в очереди необходимо упорядочить требования по не убыванию времени их обслуживания В случае одинаковых значенийвыбираем любое требование. Полученная последовательность обслуживания требованийбудет оптимальной.

Пример. Пусть в системе обслуживаются 10 требований. Время их обслуживания , а также расчетные характеристики приведены в таблице.

	1	2	3	4	5	6	7	8	9	10
	3	2	5	4	4	3	1	3	1	5
	3	5	10	14	18	21	22	25	26	31
	5	3	10	8	7	4	1	6	2	9
	10	4	31	21	17	7	1	13	2	26

При этом , а , следовательно, расписание

является лучше расписания .