10.4 Однопродуктовые модели управления запасами при детерминированном спросе Общий случай

Рассмотрим случай постоянной интенсивности спроса и поставок. Полный цикл работы системы имеет продолжительностьT. График изменения уровня запаса показан на рисунке 10.2.

Рисунок 10.2– Динамика запаса при детерминированном спросе

Обозначим через предельный запас на складе. Считая расходы на хранение и штрафы пропорциональными среднему запасу (дефициту) и времени их существования с коэффициентамиисоответственно, получаем для затрат за цикл выражение

,

где К – фиксированные расходы, связанные с запуском производства (организацией поставки). Очевидно, что текущий запас

.

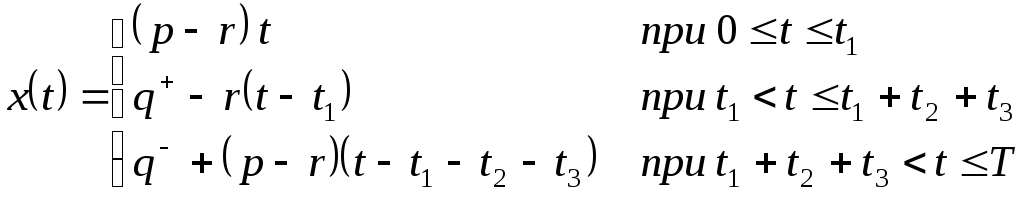Основания треугольников на рис %%%%% равны высоте, умноженной на . Соответственно

,

откуда

. (10.6)

Величина положительного запаса (площадь треугольника) равна

.

Аналогично выражается отрицательный запас (дефицит)

.

С учетом (1) затраты за цикл составят

,

а в единицу времени

.

Найдем частные производные от по ии приравняем их нулю:

.

Совместное решение этих уравнения дает для оптимальных иусловия

,

.

При этом достигается минимум затрат в единицу времени

.

Предельные варианты

Из полученных соотношений как частные случаи легко выводятся более известные формулы теории запасов.

При высоком штрафе можно принять . Тогда, следовательно

,

,

,

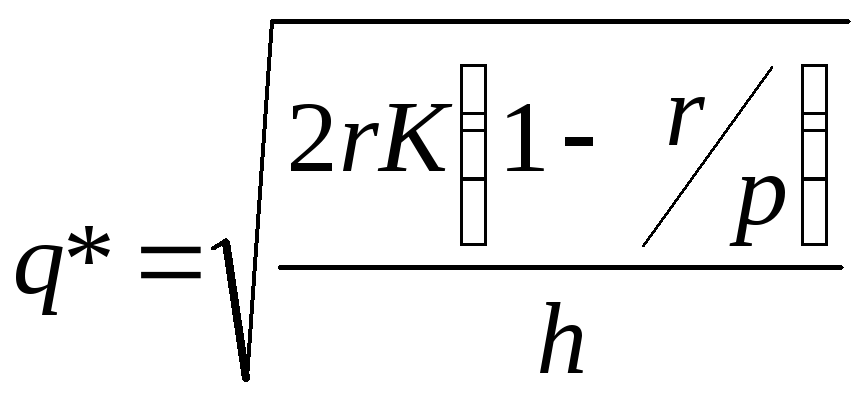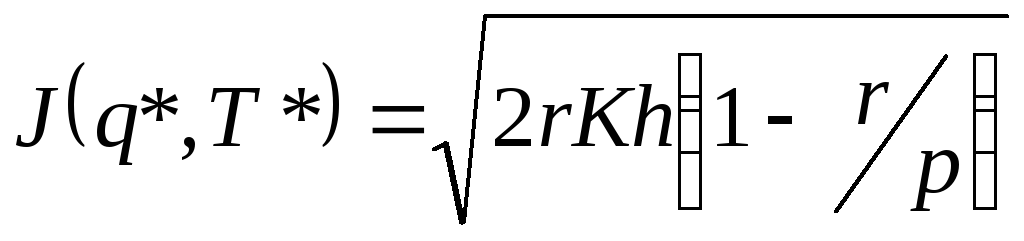а недостачи полностью исключаются.

График изменения уровня запаса показан на рисунке 10.3.

Рисунок 10.3 – Динамика запаса при отсутствии дефицита

Другой частный случай соответствует очень высокой интенсивности пополнения запаса (например, при поставке партии с вышестоящего склада). В этой модели ,и

,

.

Рисунок 10.4– Динамика запаса при мгновенной скорости поставки

Наибольшее применение получили формулы Уилсона, выведенные при обоих рассмотренных допущениях и.

,

.

График изменения уровня запаса в этом случае показан на рисунке 10.5.

Рисунок 10.5– Динамика запаса при мгновенной скорости поставки и отсутствии дефицита

Упражнения

Задача 1. Объем продажи продовольственного магазина составляет в год 900 ящиков гречневой крупы. Величина спроса равномерно распределяется в течение года. Цена покупки одного ящика равна 15 у.д.е. Доставка заказа стоит 30 у.д.е. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 1,2 у.д.е. Необходимо определить: оптимальный объём заказа; частоту заказов; точку заказа, общие затраты на управление запасами в единицу времени. Магазин работает 300 дней в году.

Задача 2. Магазин «Лада» закупает духи «Ландыш» на одной из парфюмерных фабрик. Годовой спрос на этот продукт составляет 600 шт. Издержки заказа равны 850 руб., издержки хранения – 510 руб. за одну упаковку (20 шт.) в год. Магазин заключил договор на поставку с фиксированным интервалом времени. Количество рабочих дней в году – 300. Время поставки товара – 6 дней, стоимость флакона – 135 руб.

Чему равно оптимальное число заказов в течении года? Чему равна точка восстановления запаса? Каковы минимальные совокупные издержки?

Допустим, по оценке менеджера, упущенная прибыль, связанная с отсутствием товара и утратой доверия клиентов, составляет 20 руб. в год за один флакон духов «Ландыш» при условии, что издержки заказа и хранения остаются без изменения. Определите оптимальный размер заказа при плановом дефиците. Нужно ли менеджеру вводить систему с плановым дефицитом?

Задача 3. Магазин «Все для дома» закупает линолеум размером 2×3 м² в компании «Химические товары». В зависимости от размера заказа компания предлагает следующие скидки:

Размер заказа	9 кусков или менее	10÷49 кусков	50 кусков и более
Цена одного куска, тыс. руб.	18	17,5	17,25

Издержки заказа равны 45 тыс. руб. Годовые издержки хранения составляют 50% от закупочной цены, годовой спрос на линолеум равен 100 кускам. Определить оптимальный размер заказа.

Задача 4. Мебельный салон «Антик» продает в год около 1000 спальных гарнитуров по цене 50 тыс. руб. Размещение одного заказа на поставку гарнитуров обходится в 40 тыс. руб. Годовая стоимость хранения гарнитура составляет 25% его цены. Салон может получить у поставщика скидку в 3%, если размер заказа составит не менее 200 гарнитуров. Следует ли салону воспользоваться этой скидкой?