10.3 Экономические параметры моделей управления запасами

Несмотря на разнообразие возникающих ситуаций, все задачи, связанные с функционированием простейшей системы, можно представить в общей форме.

Пусть система функционирует в течение отрезка времени . Объем спроса, предъявляемого к системе в момент, обозначим; объем поставок, приходящихся в этот же момент,. Пусть начальный запас на складе при обозначен . Тогда величина

(10.1)

характеризует объем запасов на складе в момент , если. В противном случае, если, величина, характеризует объем неудовлетворенного спроса, накопившегося к моменту.

Величину будем называтьчистым запасом. Объем поставок определяется величиной заказа, направляемой системой поставщику.

Эффективность функционирования системы тем выше, чем ниже суммарные издержки. Эти издержки связаны с различными факторами.

1. Издержки, связанные с объемом сохраняемого на складе продукта. Этот вид издержек обычно рассчитывают по простейшей линейной схеме, принимая их пропорционально текущему объему запаса. Если обозначить 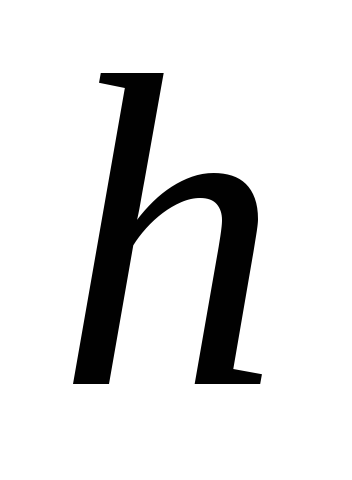плату за хранение единицы продукта в течении единицы времени, то полные издержки хранения за планируемый период функционирования системы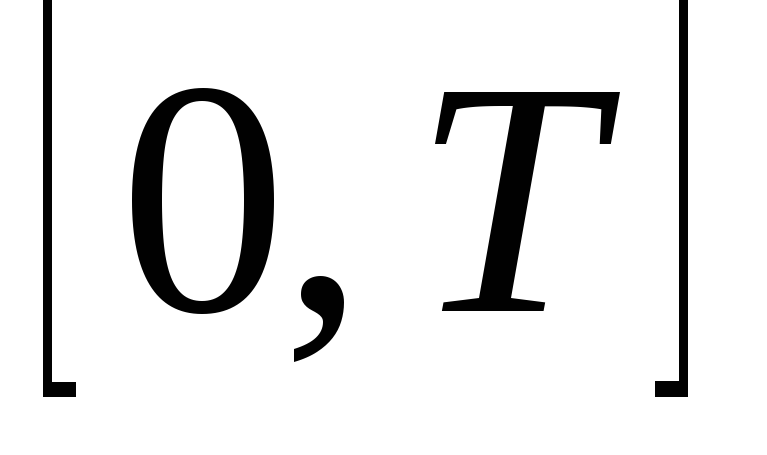оказываются равны

. (10.2)

2. Издержки из-за неудовлетворённого спроса. Оценка этих издержек является наиболее сложной и во многих случаях чисто субъективной.

Издержки существенно зависят от характера взаимоотношений между потребителем и снабжающей его системой. Для взаимоотношений между предприятиями и между внутрипроизводственными подразделениями характерно, что потребитель, получив отказ, вынужден ожидать, пока на складе не появится продукт, задолженный складом. Можно предположить, что издержки системы определяются штрафом, пропорционально объему долга, т. е. величине или.

Если коэффициент пропорциональности (коэффициент штрафа) обозначить , то общие издержки на оплату штрафа за времяравны

. (10.3)

При этом очевидно, что с увеличением срока задалживания коэффициент штрафа не увеличивается. Практически действующие правила наказания системы снабжения за несвоевременное удовлетворение спроса могут отличатся от описанных, но мы в дальнейшем ограничимся только такой формализацией.

3. Издержки, связанные с поставкой. Эти издержки определяются оформление заказа, оплатой услуг поставщика и, иногда, дополнительными транспортными расходами.

Зависимость издержек от объема заказа обычно хорошо аппроксимируются формулой

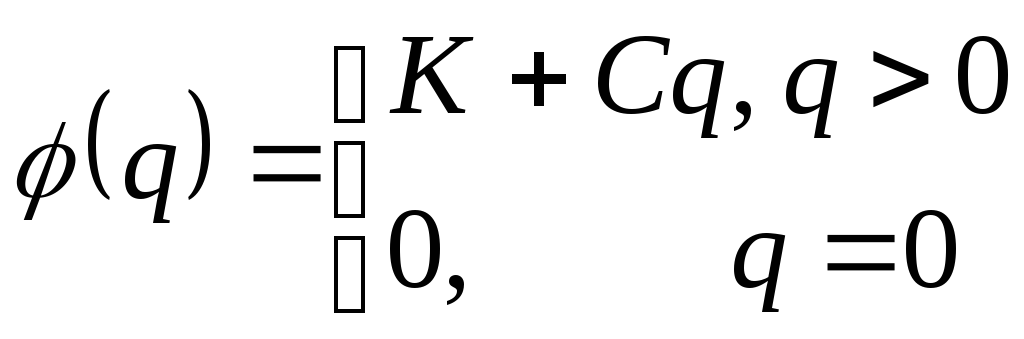. (10.4)

Величины K и C зависят от многих факторов, однако принято именовать K платой за заказ, а C – ценой поставляемого продукта. В ряде случает нелинейностью можно пренебречь, полагаяK=0.

Суммарные издержки за все заказанной в течение периода количество продукта равны, где- моменты прихода поставок.

Суммируя все указанные виды издержек, получаем

. (10.5)

Естественно, целью управления запасами является нахождение таких правил формирования заказов , чтобы суммарные издержки (10.5) были минимальны. Величинубудем называть критериальным функционалом.