Упражнения

Задача 1. Для местного аэропорта приобретается дополнительный автокар. Через три года планируется установка механизированной погрузочной системы, после чего автокары станут ненужными. Тем не менее может оказаться выгодным заменить автокар через год или два года или даже осуществить две замены (через год и через два года ). В следующей таблице приведены полные расходы (с учетом стоимости эксплуатации и выручкой от продажи), связанные с покупкой автокара в конце года i и его продажей в конце года j.

Год покупки (i)	Год продажи (j)
	1	2	3
0	4	8	15
1		5	11
2			6

Необходимо минимизировать расходы.

Сформулировать задачу как задачу выбора кратчайшего пути. Решить полученную задачу.

Задача 2. Адам Козлевич ежедневно ездит на работу на автомобиле. Закончив в свое время полный курс по теории исследования операций, он легко определил самый короткий путь от дома до работы. К сожалению, данный маршрут усиленно патрулируется нарядами полиции, и автомобиль Козлевича часто останавливают за превышение скорости (как ему кажется, не обоснованно). Таким образом, самый короткий путь оказался не самым быстрым. Поэтому А. Козлевич планирует разработать новый маршрут, на котором он имел бы самую высокую вероятность не быть остановленным полицией. Схема сети дорог, по которой Козлевич может добраться от дома до работы, показана на рисунке.

На этой же схеме приведены вероятности не быть остановленным для каждого сегмента сети дорог. Необходимо решить задачу выбора маршрута, который максимизировал бы вероятность не быть остановленным на всем протяжении маршрута.

9.2 Задача о максимальном потоке

В данном параграфе рассматривается задача определения максимального потока между двумя выделенными узлами связной сети. Каждая дуга обладает пропускными способностями в обоих направлениях, которые определяют максимальное количество потока, проходящего по данной дуге. Ориентированная (односторонняя) дуга соответствует нулевой пропускной способности.

Задачу о максимальном потоке можно свести с к задаче линейного программирования.

Пусть - поток из источника 1 в сток. Обозначив поток в дугечерезполучим следующую модель.

, (9.5)

, (9.6)

, (9.7)

, (9.8)

, (9.9)

где пропускная способность дуги.

Пропускные способности сети можно представиться в матричной форме. Для определения максимального потока из источникав стокследующий алгоритм.

Шаг 1. По заранее заданной сети выписывается матрица пропускных способностей между всеми узлами сети. Если дуга, соединяющая узлы, отсутствует, то в матрице пропускных способностей принимается .

Шаг 2. Определяется цепь, соединяющая с, по которой поток принимает положительное значение в направлении. Если такой цепи не существует, перейти к шагу 3.

Шаг 3. Пусть - способности дуг цепив направлениии.

Матрицу пропускных способностей изменить следующим образом:

а) вычесть из всех;

б) прибавить ко всем.

Заменить текущую матрицу на вновь полученную и перейти к шагу 2.

Операция (а) дает возможность использовать остатки пропускных способностей дуг выбранной цепи в направлении . Операция (б) восстанавливает исходные пропускные способности сети, поскольку уменьшение пропускной способности дуг в одном направлении можно рассматривать как увеличение ее пропускной способности в противоположном направлении.

Шаг 4. Найти максимальный поток в сети. Пусть -исходная матрица пропускных способностей, и пусть -последняя матрица, получившаяся в результате модификации исходной матрицы (шаги 1 и 2). Оптимальный поток в дугах задается как

.

Максимальный поток из вравен.

Заметим, что есть сумма всех, определенных на шаге 2. Таким образом можно объяснить, почему используются положительная разность элементов матрицидля определения результирующего потока в направлении.

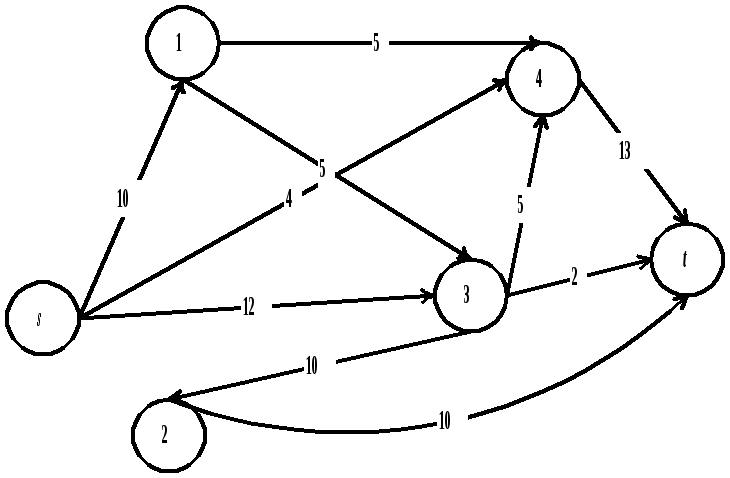
Пример. Рассмотрим сеть, с заданными пропускными способностями.

Соответствующая матрица пропускных способностей имеет вид:

		s	1	2	3	4	t
	s	0	10 -	3	14	4	0
	1	5 +	0	5	9	5 -	0
С =	2	5	6	0	15	0	10
	3	12	7	10	0	7	2
	4	3	9 +	0	8	0	13 -
	t	0	0	3	4	5 +	0

В качестве исходной цепи можно выбрать . Таким образом, элементыпомечаются знаком (-), а элементы- знаком (+). Для данной цепи максимальный поток определяется как

.

Заметим, что можно выбирать различные исходные цепи. Очевидно, что хороший выбор (вначале и на каждой итерации) должен давать наибольшее значение .

Матрица С корректируется путем вычитания из всех элементов, помеченных знаком (-), и сложения со всеми элементами, помеченными знаком (+). В результате матрица имеет вид:

		s	1	2	3	4	t
	s	0	5	3	14 -	4	0
	1	10	0	5	9	0	0
С =	2	5	6	0	15+	0	10 -
	3	12+	7	10 -	0	7	2
	4	3	14	0	8	0	8
	t	0	0	3 +	4	10	0

В качестве следующей цепи можно принять . Тогда. Следующая матрица:

		s	1	2	3	4	t
	s	0	5 -	3	4	4	0
	1	10 +	0	5	9 -	0	0
С =	2	5	6	0	25	0	0
	3	22	7 +	0	0	7 -	2
	4	3	14	0	8 +	0	8 -
	t	0	0	13	4	10 +	0

Для этой матрицы ,. Приходим к матрице

		s	1	2	3	4	t
	s	0	0	3	4	4 -	0
	1	15	0	5	4	0	0
С =	2	5	6	0	25	0	0
	3	22	12	0	0	2	2
	4	3 +	14	0	13	0	3 -
	t	0	0	13	4	15 +	0

Выбираем цепь . Тогда. Приводим матрицу:

		s	1	2	3	4	t
	s	0	0	3	4 -	1	0
	1	15	0	5	4	0	0
С =	2	5	6	0	25	0	0
	3	22 +	12	0	0	2	2 -
	4	6	14	0	13	0	0
	t	0	0	13	4 +	18	0

Следующая цепь ,. Матрица:

		s	1	2	3	4	t
	s	0	0	3	2	1	0
	1	15	0	5	4	0	0
С* =	2	5	6	0	25	0	0
	3	24	12	0	0	2	0
	4	6	14	0	13	0	0
	t	0	0	13	6	18	0

Из последней матрицы следует, что между инельзя построить цепей с положительным потоком, поскольку все элементы в столбцеравны нулю. Таким образом, это заключительная матрица.

Оптимальный поток

		s	1	2	3	4	t
	s	0	10	0	12	3	0
	1	0	0	0	5	5	0
X =	2	0	0	0	0	0	10
	3	0	0	10	0	5	2
	4	0	0	0	0	0	13
	t	0	0	0	0	0	0

Из матрицы видно, что . Сумматакже дает максимальный поток. Графический решение представимо на рисунке