
- •Содержание
- •6. Задачи теории расписаний
- •6.1 Предмет теории расписаний
- •6.2 Классификация задач теории расписаний
- •6.3 Целевые функции в задачах теории расписаний
- •6.4 Построения расписания в случае одного прибора и конечного числа требований
- •Задания для самостоятельной работы
- •6.5 Задача о двух станках
- •6.6 Алгоритм Джонсона решение задачи о двух станках
- •Задания для самостоятельной работы
- •7. Задача о назначениях венгерский метод решения
- •7.1 Постановка задачи. Некоторые свойства
- •7.2 Венгерский метод решения задачи о назначениях
- •Упражнения
- •Задания для самостоятельной работы
- •8. Метод ветвей и границ
- •3.1 Общая схема метода
- •Алгоритмическая схема метода
- •Упражнения
- •8.2 Задача коммивояжера. Метод ветвей и границ для решения задачи коммивояжера
- •Упражнения
- •Задания для самостоятельной работы
- •9. Оптимизация на сетях
- •9.1 Задача о кратчайшем пути
- •Алгоритм решения задачи о кратчайшем пути
- •Упражнения
- •9.2 Задача о максимальном потоке
- •Упражнения
- •Задания для самостоятельной работы
- •10. Модели управления запасами
- •10.1 Основные понятия теории управления запасами
- •10.2 Факторы, определяющие политику управления запасами
- •10.3 Экономические параметры моделей управления запасами
- •10.4 Однопродуктовые модели управления запасами при детерминированном спросе Общий случай
- •Предельные варианты
- •Упражнения
- •Задачи для самостоятельной работы
- •10.5 Классическая дискретная детерминированная задача управления запасами
- •10.6 Задача управления производством и запасами в случае сезонного спроса
- •Задачи для самостоятельной работы
- •10.7 Задача продавца газет
Упражнения
1. Решить рассмотренный в п. 8.2 пример, используя стратегию «левостороннего обхода дерева вариантов».
В программной реализации алгоритма метода ветвей и границ для решения задачи коммивояжера используется, как правило, левосторонний обход дерева вариантов. Отметьте преимущество этой стратегии в данном случае.
Решите задачу коммивояжера с матрицей:
|
a) |
b) |
|
|
|
|
Ответ: 1-4-6-7-3-5-2-1, L=126.
|
Ответ: 4-3-5-6-2-1-4, L=63.
|
|
с) |
d) |
|
|
|
|
Ответ: 3-1-6-5-4-2-3, L=39.
|
Ответ: 2-1-5-3-4-6-2, L=26.
|
Задания для самостоятельной работы
Определить
оптимальный маршрут в задаче с 6 городами
и матрицей затрат, построенной по
следующему правилу: Cij
= 7+(a+b+c)![]()
|
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
ai |
0 |
1 |
1 |
0 |
0 |
2 |
2 |
2 |
2 |
0 |
0 |
0 |
1 |
1 |
2 |
3 |
3 |
3 |
2 |
1 |
|
bi |
1 |
0 |
1 |
2 |
2 |
0 |
0 |
1 |
2 |
3 |
3 |
3 |
0 |
0 |
3 |
1 |
2 |
3 |
0 |
1 |
|
ci |
1 |
1 |
0 |
1 |
2 |
1 |
2 |
0 |
0 |
1 |
2 |
3 |
2 |
3 |
0 |
0 |
0 |
0 |
1 |
0 |
9. Оптимизация на сетях
9.1 Задача о кратчайшем пути
Задача о кратчайшем пути состоит в нахождении связанных между собой дорог на транспортной сети, которые в совокупности имеют минимальную длину от исходного пункта до пункта назначения.
М атематическая
модель для задачи о кратчайшем пути
строится следующим образом.
атематическая
модель для задачи о кратчайшем пути
строится следующим образом.
Каждая переменная соответствует дуге.
Каждое ограничение соответствует узлу.
Запишем задачу о кратчайшем пути как задачу линейного программирования.
Пусть
![]() ,
,
![]() - длина дуги
- длина дуги
![]() .
.
Тогда
![]() (9.1)
(9.1)
![]() , (9.2)
, (9.2)
![]() , (9.3)
, (9.3)
![]() . (9.4)
. (9.4)
Ограничения (9.2) и (9.3) отражают требования того, что в искомом пути из входа выходит одна дуга и в выход заходит одна дуга. Ограничение (9.4) обеспечивает равенство числа заходящих и выходящих в любую промежуточную вершину дуг.
Очевидно, что для дуг, вошедших в кратчайший путь, должно выполняться равенство:
![]() ,
,
для всех остальных дуг критерий правильности решения
![]() .
.
Если же
![]() ,
для которых
,
для которых![]() ,
то задача поиска кратчайшего пути не
решена, найденный путь требует пересмотра.
В данном случае вычисляются новые
,
то задача поиска кратчайшего пути не
решена, найденный путь требует пересмотра.
В данном случае вычисляются новые![]() и снова проверяется выполнение критерия
оптимального решения.
и снова проверяется выполнение критерия
оптимального решения.
Алгоритм решения задачи о кратчайшем пути
По заранее заданной сети выписывается матрица расстояний между всеми узлами сети. Если дуга, соединяющая узлы, отсутствует (отсутствует путь, ведущий из
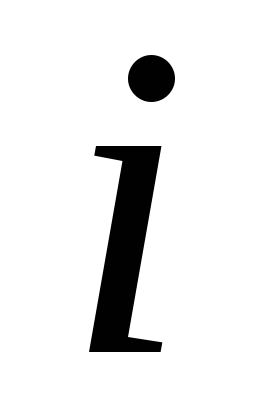 -го
пункта в
-го
пункта в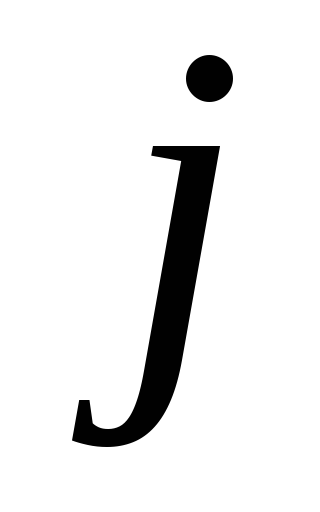 -й),
то в матрице расстояний ставится знак
запрета данного пути.
-й),
то в матрице расстояний ставится знак
запрета данного пути.Пусть
 -
сумма длин дуг, образующих цепь, ведущую
из узла 1 в узел
-
сумма длин дуг, образующих цепь, ведущую
из узла 1 в узел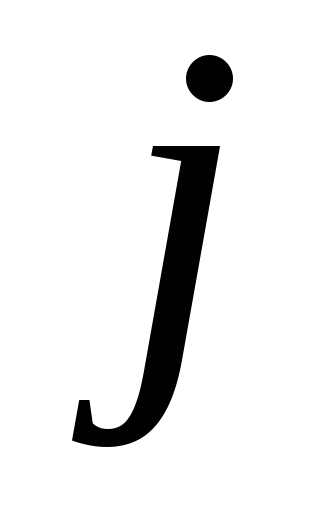 .
Положим
.
Положим и
и ,
если
,
если .
При условии, что
.
При условии, что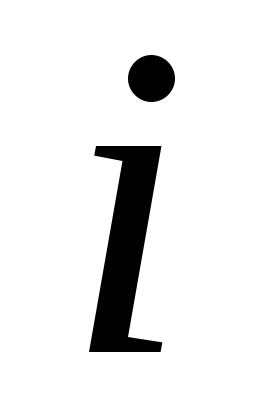 и
и соединены дугой, величина
соединены дугой, величина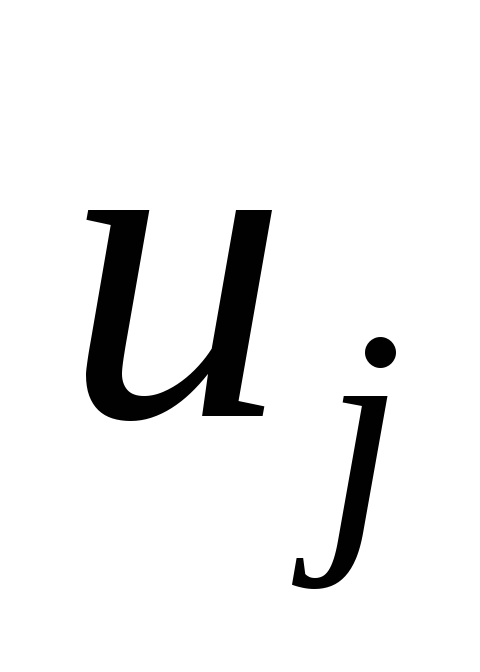 определяется как
определяется как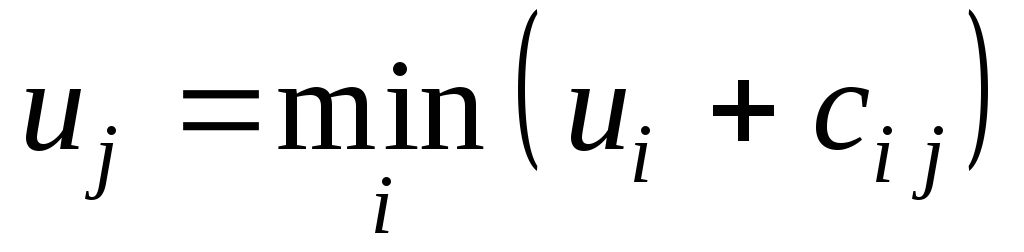 .
Процесс начинается с
.
Процесс начинается с и
и .
.Определяется кратчайший путь. Проверяется выполнение неравенства
 ,
при этом выделяют те элементы матрицы,
для которых данное неравенство
выполняется как равенство. Если для
,
при этом выделяют те элементы матрицы,
для которых данное неравенство
выполняется как равенство. Если для
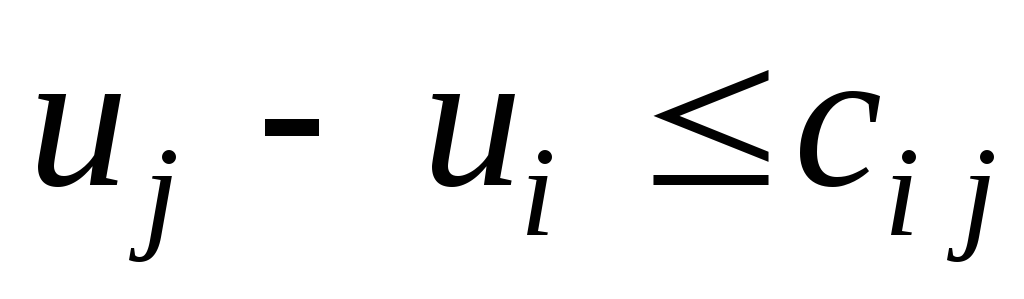 ,
то между узлами не существует более
короткого пути. Переход к п.5.
,
то между узлами не существует более
короткого пути. Переход к п.5.. Если
 ,
для которых
,
для которых ,
вычисляются новые значения
,
вычисляются новые значения ,
используя формулу
,
используя формулу .
Меняются
.
Меняются и
и для
для на
на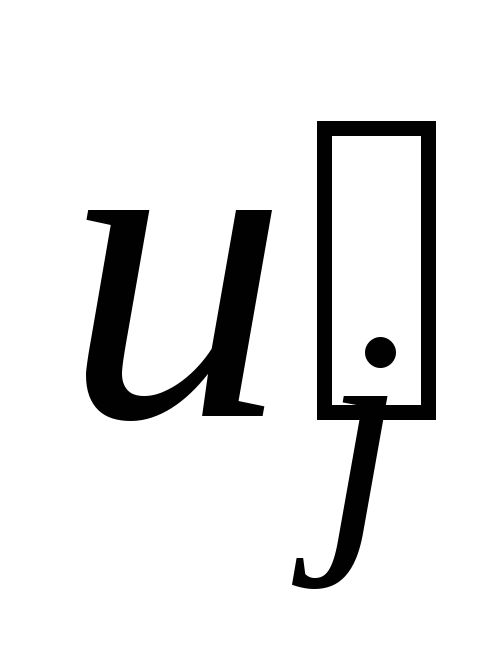 .
Повторяется п.2 с новыми значениями
.
Повторяется п.2 с новыми значениями и
и .
.Полученные
 определяют кратчайшее расстояние между
узлами 1 и
определяют кратчайшее расстояние между
узлами 1 и .
По выделенным элементам матрицы
выписывается кратчайший путь.
.
По выделенным элементам матрицы
выписывается кратчайший путь.
Пример. Рассмотрим сеть

Сеть содержит циклы, возникающие из-за возможности двустороннего движения. Если дуга ориентирована, (т.е. движение одностороннее), расстояние в другом направлении полагается равным .
Занесем данные в
матрицу расстояний, где строка
![]() (столбец
(столбец![]() )
представляет узел
)
представляет узел![]() (узел
(узел![]() ).
).
-
i j
1
2
3
4
5
6
7

1
2
8
11
9
0
2
4
3
5
1
2
3
1
4
2
5
4
5
9
2
23
11
5
2
7
9
7
6
8
3
5
1
10
3
7
10
4
2
13
 j
j0
2
5
11
7
3
13
Исходные величины
![]() и
и![]() определяются следующим образом. Пусть
определяются следующим образом. Пусть![]() .
При использовании формулы
.
При использовании формулы
![]()
![]()
осуществляется
последовательное обращение к величинам
![]() и
и![]() по мере того, как они становятся
доступными.
по мере того, как они становятся
доступными.

При переходе к
шагу 2 проводится проверка условия
оптимальности путем сравнения
![]() с
с![]() .
При этом выделяются те элементы, для
которых
.
При этом выделяются те элементы, для
которых![]() =
=![]() .
.
-
i j
1
2
3
4
5
6
7

1
2
8
11
9
0
2
4
3
5
1
2
3
1
4
2
5
4
5
9
2
23
11
5
2
7
9
7
6
8
3
5
1
10
3
7
10
4
2
13

0
2
5
11
7
3
13
В процессе реализации
алгоритма обнаруживается, что условие
оптимальности первый раз нарушается
при
![]() для
для![]() и 5. Величины
и 5. Величины![]() и
и![]() меняются следующим образом:
меняются следующим образом:
![]()
После этого
повторяется шаг 2 с измененными значениями
![]() и
и![]()
-
i j
1
2
3
4
5
6
7
1
2
8
11
9
0
2
4
3
5
1
2
3
1
4
2
5
4
5
9
2
23
11
(8)
5
2
7
9
7
(4)
6
8
3
5
1
10
3
7
10
4
2
13

0
2
5
11
7
3
13
(8)
(4)
Из последней
таблицы видно, что в новых изменениях
нет необходимости, и поэтому последние
измененные величины
![]() дают длину кратчайшего пути от 1 до
дают длину кратчайшего пути от 1 до![]() .
Кратчайшее расстояние между узлами 1 и
7 равно
.
Кратчайшее расстояние между узлами 1 и
7 равно![]() (=13).
(=13).
Найдем участки
кратчайшего пути между узлами 1 и 7.
Определение участков пути должно
начинаться с узла 7. Из столбца 7 видно,
что равенство выполняется (подчеркнутый
элемент) при
![]() и
и![]() ,
т.е. либо узел 5, либо узел 6 соединены с
7 (альтернативные решения). Аналогичные
исследования для 5 и 6 узлов дадут
,
т.е. либо узел 5, либо узел 6 соединены с
7 (альтернативные решения). Аналогичные
исследования для 5 и 6 узлов дадут![]() и
и![]() .
Будем продолжать эту процедуру до тех
пор, пока не вернемся в первый узел.
.
Будем продолжать эту процедуру до тех
пор, пока не вернемся в первый узел.
Таким образом, кратчайший путь имеет вид:





