Алгоритмическая схема метода

Решается задача вида: .

Шаг 1. Инициализация.

Задать начальное рекордное значение R. Если отыскание начального рекорда затруднительно, положить Положить– множество номеров подмножеств, подлежащих ветвлению, — множество номеров подмножеств, для которых будут решаться оценочные задачи.

Шаг 2. Вычисление оценок.

Решить оценочные задачи для множеств где. Вычислить

Шаг 3. Обновление рекорда.

Если на шаге 2 получены допустимые точки , то положитьR=.

Шаг 4. Сокращение перебора.

Осуществить закрытие неперспективных множеств (включая те номера , для которых). Удалить их номера из множествI и J. Положить ,. Если, то перейти к шагу 7.

Шаг 5. Реализация стратегии.

Выбрать из множества I номер k – индекс подмножества ,подлежащего ветвлению на данном этапе в соответствии с зафиксированным правилом.

Шаг 6. Ветвление.

Осуществить разбиение множества на подмножества .Положить . Перейти к шагу 2.

Шаг 7. Останов, .

Заметим, что такая последовательность шагов может быть не рациональной в случае, если при вычислении оценок заведомо не могут появиться допустимые точки (например, при решении задачи коммивояжера).

Упражнения

1. Докажите свойство монотонности оценок в условиях, при которых ветвление и составление оценочных задач осуществляется по правилам, указанным в п.п. 1 и 2 описания основных модулей.

2. Предложите другие стратегии обхода дерева вариантов.

3. Докажите, что при использовании основного правила отбрасывания неперспективных множеств (п.4) не происходит потери решения.

4. В предложенной алгоритмической схеме отыскивается одно решение, даже если оно в задаче не единственно. Где происходит потеря других решений? Исправьте алгоритм таким образом, чтобы появилась возможность отыскания всех решений задачи.

8.2 Задача коммивояжера. Метод ветвей и границ для решения задачи коммивояжера

Постановка задачи коммивояжера состоит в следующем. Имеется городов. Задана матрица расстояний между ними: . Cчитаем, что . В общем случае возможно, что. Кроме того, будем полагать, что. Ищется кратчайший замкнутый маршрут (цикл), проходящий через каждый город ровно один раз и минимизирующий суммарное пройденное расстояние. Математическая постановка задачи может быть записана, например, следующим образом.

В этой постановке не учитывается естественное требование связности маршрута (отсутствия подциклов), но в дальнейшем оно будет выполняться алгоритмически.

Определение. Матрица называется приведенной, если все ее элементы неотрицательны, а каждая строка и каждый столбец содержат по крайней мере по одному нулевому элементу.

Приведение матрицы может быть осуществлено следующим образом. Пусть имеется матрица . Найдем Получим матрицу, которая в каждой строке содержит нулевые элементы. Найдем далееПолученная матрицаявляется приведенной, а сумманазывается суммой приводящих констант.

Матрица определяет новую задачу коммивояжера, которая в качестве оптимального решения будет иметь ту же последовательность городов. Между величинамии(длинами оптимальных маршрутов) будет существовать следующее соотношение:. Отсюда следует очевидное неравенство: , то есть сумма приводящих констант является нижней оценкой целевой функции исходной задачи коммивояжера.

Конкретизируем теперь основные этапы метода ветвей и границ применительно к данной задаче.

Пусть — множество всех возможных маршрутов.

1. Ветвление. При ветвлении очередное множество разбивается на два подмножества следующим образом. В матрице, соответствующей разветвляемому множеству, для каждого нулевого элементавычисляется число. Затем определяется пара индексов, такая что. Первое подмножествоформируется добавлением условия(из-го города идти в-й), второе подмножествосодержит условие.

2. Вычисление оценок. Пусть в соответствии с предыдущим пунктом произведено разбиение . Рассмотрим правило перехода от матрицык матрицами. Матрицасодержит те же строки и столбцы, что и. Положим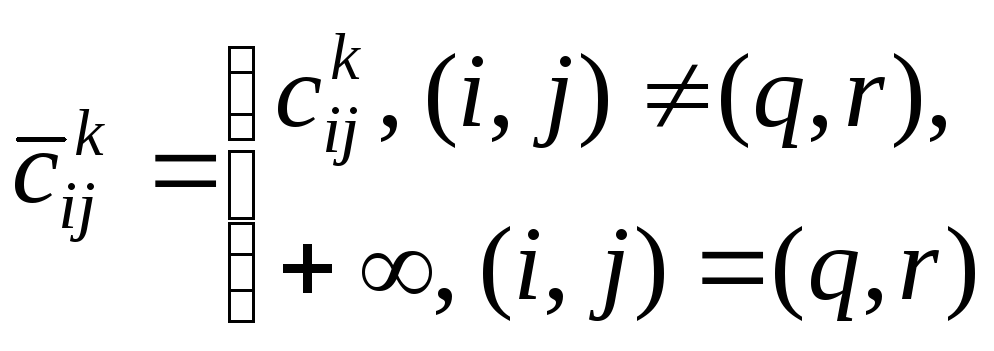. Применяя к полученной матрице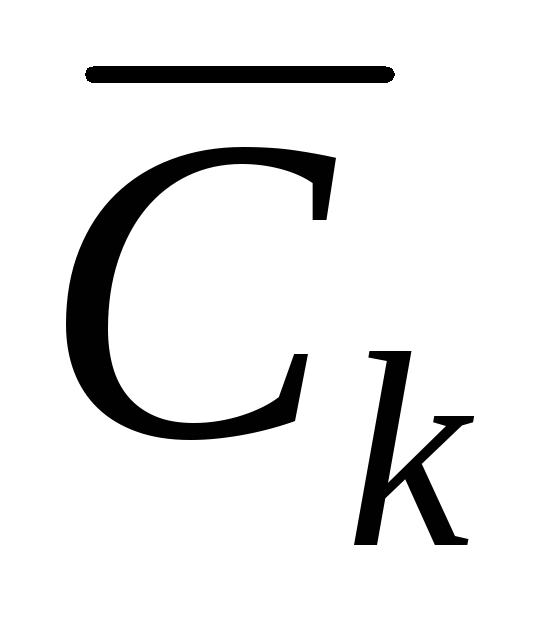процедуру приведения, получим матрицу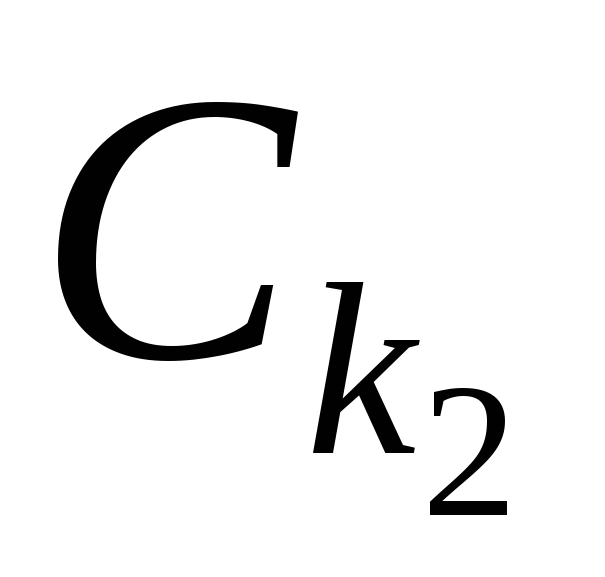. При этом сумма приводящих констант будет равна. Таким образом, оценкой множествабудет. Определим теперь правило построения матрицы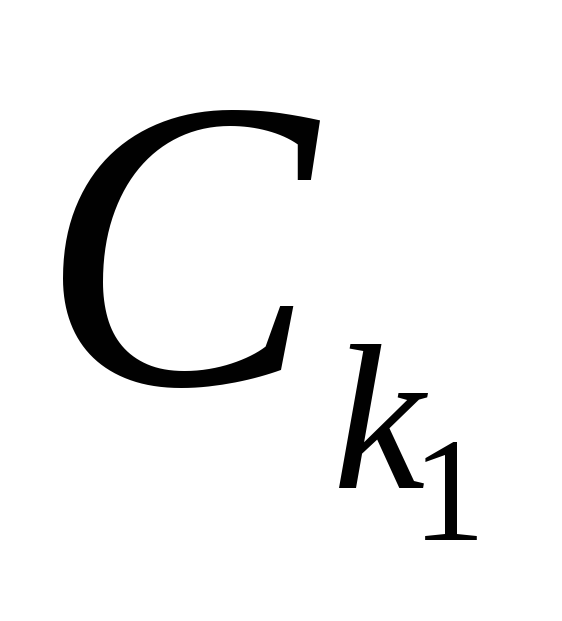. По определению, множествозаведомо содержит переход из-го города в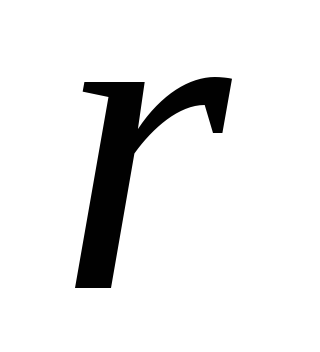-й. Поэтому в матрицеследует вычеркнуть-ю строку и-й столбец. Далее следует запретить возможность возникновения подциклов (замыкания фрагментов маршрута). С этой целью полагаем равнымивсе элементы, введение которых в маршрут даст наличие подцикла (например,). К полученной в результате матрице следует применить процесс приведения и, найдя сумму приводящих констант, посчитать оценку.

Правило обхода дерева вариантов, выбор перспективного множества при ветвлении и проверка критерия оптимальности осуществляются в соответствии с общей схемой метода ветвей и границ.

Схема метода ветвей и границ для задачи коммивояжера

Шаг 1. Определение начального рекорда. (При отсутствии дополнительной информации можно взять длину любого маршрута). Приведение исходной матрицы. Задать k=0.

Шаг 2. Выбор пары .

Шаг 3. Ветвление .

Шаг 4. Преобразование матрицы . Вычисление матрици. Если какая-то из этих матриц имеет размер 22, то переход к шагу 7.

Шаг 5. Вычисление оценок и.

Шаг 6. Выбор перспективного множества в соответствии со стратегией. ПоложитьПереход к шагу 2.

Шаг 7. Получение допустимого маршрута, возможная смена рекорда и сокращение перебора.

Шаг 8. Проверка критерия оптимальности. Если он выполнен, то останов. Иначе переход к шагу 6.

Замечание. В момент получения матрицы 22 определяется замыкающая пара городов для образования допустимого маршрута.

Пример. Рассмотрим задачу коммивояжера с и матрицей расстояний

.

Выберем стратегию «по минимуму оценки». Положим . Осуществив операцию приведения, получаем матрицу.

В последнем столбце и нижней строке записаны приводящие константы. Их сумма S=10, то есть . Для каждого нулевого элемента матрицы считаем : ,. Имеем. Следовательно,. Формируем множестваи, добавляя соответственно условияи. Вычисляем матрицыи.

Считаем оценки: , . В таком случае дальнейшему ветвлению подлежит множество . Для каждого нулевого элемента матрицысчитаем: . Имеем . Следовательно,.

Формируем множества и, добавляя соответственно условияи. Вычисляем матрицыи.

Вычисляем оценки: , .

В соответствии со стратегией дальнейшему ветвлению подлежит множество , так как оно имеет наименьшую оценку . Аналогично для всех нулевых элементов матрицы считаеми определяем, что. Формируем множестваи, добавляя соответственно условияи. Матрицыиимеют вид:

Вычисляем оценки: , . Дальнейшему ветвлению подлежит множество .

Делим на подмножестваипо паре. Рассчитав матрицыи, определяем , . Минимальную оценку 16 имеет три подмножества: и.

Выберем для дальнейшего ветвления . Делим его на подмножестваипо паре. Получим , .

Далее делим на подмножестваипо паре. Вычисляем , .

Делим по паренаи. При этом получаем матрицуразмера 22. В результате выписываем допустимую точку (матрицуX)

со значением целевой функции .

Соответствующий маршрут: 1-2-3-5-4-8-7-5-1.

Меняем рекорд: , и подмножествавыбрасываются из рассмотрения как неперспективные (их оценки превышают или равны рекордному значению). Так как больше подмножеств для ветвления не осталось, то найденная точка является оптимальным решением. Однако оно может быть не единственным, так как подмножестватак же имеют оценку 16. Чтобы выяснить, существуют ли другие решения, нужно осуществлять дальнейшее ветвление этих множеств.

Дерево вариантов в рассмотренном примере имеет следующий вид.