26. Давление газа на стенки сосудов.

Мы знаем, что газы, в отличие от твёрдых тел и жидкостей заполняют весь сосуд, в котором они находятся, например стальной баллон для хранения газов, камеру автомобильной шины или волейбольного мяча. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твёрдого тела на опору. Известно, что молекулы газа беспорядочно движутся. При своём движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, потому и число их ударов очень велико. Хотя сила удара отдельной молекулы мала, но действие всех молекул о стенки сосуда значительно, оно и создаёт давление газа. Итак, давление газа на стенки сосуда (и на помещённое в газ тело) вызывается ударами молекул газа. При уменьшении объёма газа его давление увеличивается, а при увеличении объёма давление уменьшается при условии, что масса и температура газа остаются неизменными. Давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа не меняется.

27. Средняя кинетическая энергия поступательного движения молекул идеального газа.

Средняя кинетическая энергия поступательного движения молекулы идеального газа

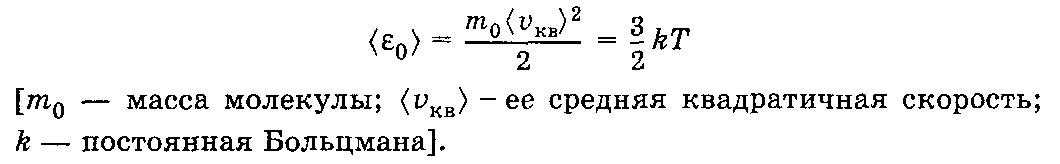
28. Распределение Максвелла. Виды скоростей молекул и их физический смысл.

Распределение Максвелла

Молекулы газа вследствие теплового движения испытывают многочисленные соударения друг с другом. При каждом соударении скорости молекул изменяются как по величине, так и по направлению. В результате в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям, зависящее от абсолютной температуры Т. При этом все направления векторов скоростей молекул оказываются равноправными (равновероятными), а величины скоростей подчиняются определенной закономерности. Распределение молекул газа по величине скоростей называется распределением Максвелла.

Если одновременно измерить скорости большого числа N молекул газа и выделить некоторый малый интервал скоростей от v до v+v, то в выделенный интервалv попадает некоторое числоN молекул. На графике удобно изображать зависимость величиныот скорости v. При достаточно большом числе N эта зависимость изображается плавной кривой, имеющей максимум при(наиболее вероятная скорость). Здесь m - масса молекулы,- постоянная Больцмана.

Характерным параметром распределения Максвелла является так называемая среднеквадратичная скорость означает среднее значение квадрата скорости. В молекулярной физике доказывается, что

где - молярная масса.

Из выражения для среднеквадратичной скорости следует, что средняя кинетическая энергия поступательного движения молекул газа есть

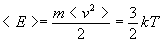
Распределение Максвелла является одной из важнейших статистических закономерностей молекулярной физики.

Скорости молекул подразделяются на:

1) наиболее вероятную ,

2) среднюю ,

3) среднюю квадратичную 

29. Распределение Больцмана. Барометрическая формула.

Барометрическая формула. Если температура не зависит от высоты, то давление газа меняется с высотой по закону: , где— высота,— молярная газовая постоянная,— постоянная Больцмана,— ускорение свободного падения вблизи поверхности земли,— молярная масса газа,— масса одной молекулы,— абсолютная температура.

Поделив барометрическую формулу на , с учетом уравнения состояния идеального газа, получим распределение Больцмана — зависимость концентрации молекул от потенциальной энергии: , где  — потенциальная энергия молекулы. В однородном поле силы тяжести .

Exp, как я поняла, это «экспериментальное»???????????????