2.10. Теорема. (Свойства произведения матриц).Операция умножения матриц обладает следующими свойствами:

1°. (AB)C=A(BC) – ассоциативность, если определены произведения матриц AB и (AB)C, то определены и произведения BC и A(BC), причём (AB)C = A(BC).

2°. A(B+C) = AB+AC – дистрибутивность умножения относительно сложения,

3°. ( A) B = A (B) = (AB),

4°. A = A; AE = A,

выполненными для любых матриц , для которых левые части равенств имеют смысл.

2.11. Матрицы и, для которых, называютсяперестановочными или коммутирующими.

2.12. Если А – квадратная матрица, то определено произведение АА, которое называется квадратом матрицы А, обозначается А², и также является квадратной матрицей того же порядка, что и А. Поэтому определено и произведение АА². Вообще, если для квадратной матрицы определена степень , то по определению. Если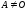, то по определению считается, чтоA⁰=E.

2.13. Теорема. Натуральные степени квадратной матрицы обладают следующими свойствами:

1°. ;

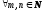
2°..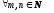

2.14. Пусть — произвольный многочленn-й степени. Многочленом от матрицы A называется матрица

.

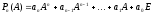Все алгебраические операции, определенные для многочленов, определены и для многочленов от матрицы. Многочлены от матрицы — перестановочные матрицы: P_n(A)·Q_m(A) = Q_m(A)·P_n(A).

2.15. Матрица А называется нильпотентной степени , если существует такое целое число , чтои.

2.16. Пусть . Матрица называетсятранспонированной к матрице 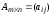, если

, .

Таким образом, из определения мы видим, что при транспонировании матрицы строки становятся столбцами и наоборот.

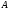Кроме обозначения A^T для матрицы, транспонированной к А, ещё используют следующие: . Переход от матрицык матриценазываетсятранспонированием матрицы.

2.17. Теорема. (Свойства операции транспонирования). Операция транспонирования обладает следующими свойствами:

1°.;

2°.;

3°.,;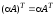

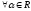4°.,

выполненными для всех матриц , для которых имеют смысл левые части равенств.

Заметим, что при транспонировании блочной матрицы транспонированию подлежат и ее элементы. Например,

.

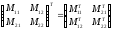2.18.Квадратная матрица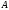называетсясимметрической (симметричной), если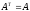. Квадратная матрицаназываетсякососимметрической (кососимметричной), если. Любую квадратную матрицуможно представить, и при этом единственным образом, в ви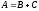де, где-симметрическая, а-кососимметрическая матрицы.

2.19.Матрица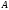называетсяортогональной, если.

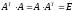2.20. Пусть даны квадратные матрицыи.Прямой суммойматрициназывают квадратную блочную матрицупорядка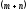, равную, где обозначает нулевой блок.

Обозначение: .

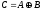2.21. Теорема.(Основные свойства прямой суммы матриц).

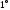. Прямая сумма ассоциативна: .

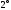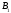. Пусть квадратные матрицы иимеют порядок, а квадратные матрицыиимеют порядок. Тогда

,

.

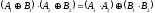2.22. Пусть даны матрицы 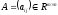и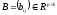. Кронекеровым (тензорным) произведением матриц иназывают матрицуразмеров, равную

.

Обозначение: .

Таким образом, из определения мы видим, что 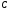есть блочная матрица, составленная из блоков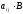, где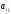- элементы матрицы.

2.23. Теорема.(Основные свойства кронекерова произведения матриц).

.При условии существования произведений и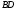имеет место равенство

,

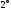. При транспонировании матриц

.

2.24. Элементарными преобразованиями матрицы называются преобразования следующих типов:

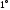умножение строки (столбца матрицы на число, отличное от нуля;

перестановка двух строк (столбцов) матрицы;

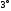прибавление к одной строке (столбцу) матрицы другой ее строки (соответственно столбца), умноженной на любое число.

Каждое элементарное преобразование строк (столбцов) матрицы 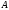можно трактовать как умножение матрицыслева (справа) на матрицу специально вида. Эта матрица получается, если то же преобразование вы полнить над единичной матрицей.

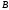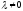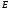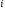Пусть матрица получается в результате умножения-строки матрицына число. Тогда, где матрицаполучается из единичной матрицыпорядкаумножением ее-й строки на число.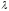

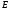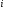Пусть матрица получается в результате перестановки-й и-й строк матрицы. Тогда, где матрицаполучается из единичной матрицыпорядкаперестановкой ее-й и-й строк.

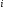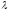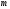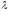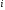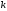Пусть матрица получается в результате добавления к-й строке матрицыее-й строки с коэффициентом. Тогда, где матрицаполучается из единичной матрицыпорядкав результате добавления к-й строке ее-й строки с коэффициентом, т.е. в матриценулевой элемент на пересечении-й строки и-го столбца заменен на число.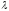

С помощью алгоритмов, которые основаны на элементарных преобразованиях строк и столбцов, матрицы можно преобразовывать к различному виду.

2.25. Теорема (об основном процессе). Произвольная ненулевая матрица конечным числом элементарных преобразований только строк может быть приведена к верхней ступенчатой форме.