Часть 1.Определения и формулировки теорем

1. Матрицы и линейные операции над ними

1.1. Пусть .Матрицей размера 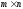(читается m на n) или -матрицей называется совокупность чисел, записанная в виде прямоугольной таблицы изстрок истолбцов. При этом сами числа называютсяэлементами матрицы. Матрицу обозначают прописными латинскими буквами, при этом саму таблицу заключают в скобки (либо круглые, либо квадратные, либо двойные вертикальные):

; ;.

Элементы матрицы обозначают строчными буквами, снабженными двумя индексами: - элемент матрицы, расположенный в-й строке и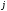-м столбце (в позиции). В этих обозначениях матрицы в общем виде могут быть записаны следующим образом:

.

Матрица А имеет размеры ,B – , aC – .

Удобно также пользоваться обозначениями:

- множество всех вещественных матриц размера ;

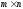- матрица с элементами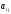в позиции,

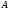- элемент матрицы в позиции;

-матрица размера .

Часто вместо только нижних индексов удобнее использовать верхний и нижний индексы. Условимся о правиле соответствия этих двух записей: первый индекс соответствует верхнему индексу, второй индекс соответствует нижнему индексу, т.е. или.

1.2. Набор называют-строкой, а набор--столбцом матрицы().

Матрица размера 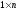называетсяматрицей-строкой, или строкой, или вектор-строкой, а размера матрицей-столбцом, или столбцом, или вектор-столбцом.

1.3. Матрица называется нулевой и обозначается O, если все её элементы равны нулю.

1.4. Если m=n, то матрица называетсяквадратной, а число n называется её порядком (говорят: квадратная матрица А n-го порядка).

1.5. Элементы 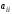квадратной матрицы образуют её главную диагональ и называютсядиагональными. Если в квадратной матрице все недиагональные элементы равны нулю (при), а отличными от нуля могут быть только диагональные элементы (среди них также могут быть нули), то такая матрица называетсядиагональной. Обозначение:. Диагональная матрица, у которой все диагональные элементы равны между собой, называетсяскалярной. Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной (тождественной) и обозначается символам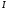и или. Единичная матрица выглядит так:

.

Если обозначить элементы единичной матрицы , то

.

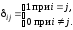Символ , равный 1, когда индексы совпадают, и 0, когда они разные, широко применяется как в математике, так и в физике, и называетсясимволом Кронекера. Таким образом, элементы единичной матрицы совпадают с соответствующими символами Кронекера.

1.6. Квадратная матрица называетсяверхней треугольной, если при,нижней треугольной, если при. Неквадратная матрицаприn>m называется трапециевидной, если приi>j. Например, А – верхняя треугольная, В – нижняя треугольная, С – трапециевидная матрицы:

;

1.7.Число(или) называетсяследом матрицы.

1.8.Разобьем матрицусистемой горизонтальных и вертикальных линий на клетки (блоки).Клеточной(блочной) матрицей называется матрица, элементами которой служат эти клетки.

Например, матрица В разбита на 4 блока, а матрица С – на 6:

, .

Общий вид клеточной матрицы:

,

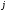где - клетка, расположенная в-клеточной строке и в-клеточном столбце. Блочные матрицы продуктивно используются в вычислительной математике для обработки большого объема информации.