Метод распознавания состояния объектов, основанный на теореме Байеса.

Этот метод основан на том, что имеется некоторая доопытная вероятность в постановках диагностирования, т.е. априорно известны вероятности диагностирования для однотипных объектов, находящихся в одинаковых условиях.

Пусть имеется некоторый объект, состояние которого характеризуется признаком k_j [7]. Известно, что этот признак может проявляться как при наличии диагноза D_j, так и при его отсутствии. Появление признака k_j является случайным, но статистически зависимым от наличия диагноза D_i.

Вероятность совместного появления событий (наличия у объекта состояния D_i и признака k_j) равна:

, (2.8)

где р(D_i) – априорная вероятность диагноза, определенная по статистическим данным;

p(k_j/D_i) – вероятность появления признака k_j у объектов с состоянием D_i;

p(k_j) – вероятность появления признака k_j во всех объектах независимо от их состояния.

Из равенства ( 2.8) вытекает теорема Байеса:

, (2.9)

где n – число состояний объекта.

Если каждое из n состояний объекта характеризуется комплексом признаков К*={k₁, k₂…k_m}, то формула Байеса примет вид:

, (2.10)

где .

Решающее правило при постановке диагноза выглядит следующим образом:

. (2.11)

Основным недостатком метода Байеса является увеличение погрешности при распознавании редких диагнозов.

Метод последовательного анализа.

Суть метода последовательного анализа заключается в том, что в процессе диагностирования объекта, состояние которого характеризуется несколькими признаками, все признаки последовательно проверяются. На каждом шаге процедуры диагностирования проверяется условие о возможности постановки диагноза. Если информации достаточно, то ставится диагноз и диагностирование прекращается. В противном случае проверяется следующий признак и т.д. проб являются случайными величинами, то одной пробы для определения состояния изоляции не достаточно.

Пусть объект может находиться в двух состояниях: D₁ – исправное состояние (в нашем случае это состояние соответствует незагрязненной изоляции) и D₂ – неисправное состояние (загрязненная изоляция). Пусть в результате первой пробы получен признак, характеризующий состояние объекта x₁, причем, этот признак при диагнозе D₂ встречается чаще, чем при диагнозе D₁. При этом, если

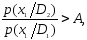то , (2.12)

где А – верхняя граница принятия решения.

В противном случае, когда признак k₁ значительно чаще встречается при диагнозе D₁, принимается решение

при , (2.13)

где В – нижняя граница принятия решения.

Отношение вероятностей

(2.14)

называют отношением правдоподобия.

Если в результате первой проверки условие (2.14) выполняется, то необходима следующая проверка и т.д. Отношение правдоподобия для n-ой проверки будет выглядеть следующим образом:

. (2.15)

Расчеты повторяются до тех пор, пока значение отношения не выйдет за одну из указанных границ.

Границы А и В рассчитываются исходя из вероятностей ошибок первого и второго рода, которые считаются заданными:

,

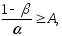
где  - ошибка первого рода – это принятие решения о наличии дефекта, когда в действительности система находится в исправном состоянии;

 - ошибка второго рода – принятие решения об исправном состоянии, в то время как система содержит дефект.

Значения ирекомендуется выбирать из диапазона 0,05…0,10.