
- •Численные методы
- •Решение трансцендентных и алгебраических уравнений
- •Постановка задачи
- •Метод половинного деления
- •Метод хорд
- •Метод итераций
- •Метод Ньютона
- •Модифицированный метод Ньютона
- •Метод секущих
- •Интегрирование функций Постановка задачи
- •Формула прямоугольников
- •Алгоритм программы метода прямоугольника
- •Формула трапеций
- •Формула Симпсона
- •Квадратурная формула Чебышева
- •Квадратурная формула Гаусса
- •Методы решения слау Постановка задачи
- •Метод Крамера
- •Метод Гаусса
- •Связь метода Гаусса с lu-факторизацией
- •Вычисление определителя
- •Обращение матрицы
- •Алгоритм схемы Халецкого
- •Вычисление невязки решения
- •Итерационные методы
- •Теорема Самарского о сходимости стационарных методов
- •Метод Якоби
- •Алгоритм метода Якоби
- •Возможные ошибки
- •Теорема сходимости метода Якоби
- •Рекомендации
- •Метод Зейделя
- •Интерполяционный многочлен Лагранжа
- •Интерполяционная формула Ньютона.
- •Интерполяционные и экстраполяционные формулы при равноотстоящих значениях аргумента.
- •Формула Ньютона для интерполирования вперед и экстраполирования назад
- •Формула Ньютона для интерполирования назад и экстраполирования вперед
- •Интерполяционные формулы Гаусса.
- •Построение кривой по точкам Общие понятия
- •Метод наименьших квадратов
- •Метод линеаризации данных по методу наименьших квадратов.
- •Интерполирование сплайнами Кусочно-линейное и кусочно-квадратичное интерполирование
- •Простейший подход к сглаживанию
- •Кусочно-кубические сплайны
- •Список литературы
Интерполяционный многочлен Лагранжа
Пусть на отрезке [a,b] заданы (n+1) точка x0, x1, , xn и значения функции f в этих точках.
Будем
строить интерполяционный многочлен
вида
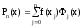 ,
где
,
где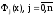 -
многочлены степениn,
удовлетворяющие условиям
-
многочлены степениn,
удовлетворяющие условиям
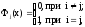
так
как требуем, чтобы значения интерполяционного
многочлена и значения функции f(x)
совпадали в узлах интерполяции i,
т.е.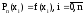 .
.
Тогда
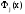 можно искать в виде:
можно искать в виде:
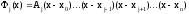
где
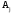 - некоторая константа, которую найдем
из условия
- некоторая константа, которую найдем
из условия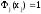 ,
тогда
,
тогда
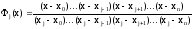
Если
обозначить
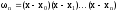 и продифференцировать это выражение
по х, полагая х=хj,
то последнее выражение можно записать
в виде:
и продифференцировать это выражение
по х, полагая х=хj,
то последнее выражение можно записать
в виде:
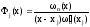 ,
,
где
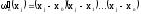
Таким образом, получим многочлен
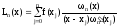 ,
,
который называется интерполяционным многочленом Лагранжа.
Пусть
узлы интерполирования являются
равноотстоящими, т.е.
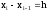 ,
если ввести новую переменную
,
если ввести новую переменную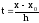 ,
то многочлен Лагранжа для равноотстоящих
узлов запишется в виде
,
то многочлен Лагранжа для равноотстоящих
узлов запишется в виде
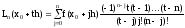 ,
,
т.к.
 .
.
Оценка
погрешности интерполяционного многочлена
Лагранжа: если функция f(x)
имеет на [a,b]
непрерывные производные (n+1)-го
порядка, имеет вид
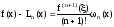 ,
где
- некоторая точка [a,b]
или
,
где
- некоторая точка [a,b]
или
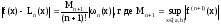 .
.
Это
выражение может служить оценкой
отклонения полинома Лагранжа от f(x)
в том случае, когда можно оценить
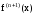 .
.
Интерполяционная формула Ньютона.
Запишем интерполяционный многочлен Лагранжа Ln(x) в другой форме:
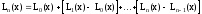
где
разность
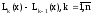 ,
есть многочлен степениk,
обращающийся в нуль в точках x0,,xk-1.
Поэтому можно записать
,
есть многочлен степениk,
обращающийся в нуль в точках x0,,xk-1.
Поэтому можно записать
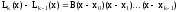
Константу B найдем, полагая x=xk, т.е.
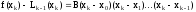
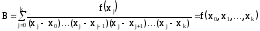
где
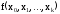 -
есть разностное отношениеk-го
порядка .
-
есть разностное отношениеk-го
порядка .
Учитывая выражение для В интерполяционный многочлен можно представить в виде

Эта форма записи интерполяционного многочлена Лагранжа носит название интерполяционного многочлена Ньютона для неравных промежутков. Многочлен Ньютона имеет степень равную n и удовлетворяет условию
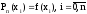 .
.
Формула
Ньютона имеет более сложное строение,
чем формула Лагранжа, и требует составления
разностных отношений
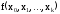 ,
,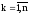 .
Несмотря на это, она более удобна для
вычислений, т.к. при добавлении нового
узла все проделанные вычисления
сохраняются, а в формуле добавляется
еще одно слагаемое
.
Несмотря на это, она более удобна для
вычислений, т.к. при добавлении нового
узла все проделанные вычисления
сохраняются, а в формуле добавляется
еще одно слагаемое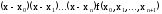 .
.
Это позволяет не задавать заранее число узлов интерполирования, а постепенно увеличивать точность результата, добавляя последовательно по одному новому узлу.
Остаточный член формулы Ньютона совпадает с остаточным членом формулы Лагранжа, т.е.
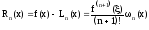
где - точка отрезка, содержащего узлы интерполирования и точку х. Из свойств разностных отношений следует
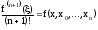 .
.
Тогда
для остаточного члена имеем:
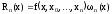 .
.
Интерполяционные и экстраполяционные формулы при равноотстоящих значениях аргумента.
Пусть все узлы интерполирования хi принадлежат отрезку [a,b], причем а=х0, b=xn.
Если точка интерполирования х принадлежит отрезку [a,b], то формула, приближающая функцию f в точке х, называется интерполяционной, а если х не принадлежит отрезку [a,b], то формула называется экстраполяционной.
Узлы
интерполирования, лежащие ближе к точке
интерполирования, оказывают большее
влияние на интерполяционный многочлен,
чем узлы, лежащие дальше. Поэтому
целесообразно за
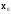 и
и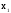 брать ближайшие к х узлы интерполирования
и проводить сначала линейную интерполяцию
по этим узлам, а затем постепенно
привлекать следующие узлы таким образом,
чтобы они возможно симметричнее
располагались относительно точки.
Полученные при этом поправки будут
незначительными.
брать ближайшие к х узлы интерполирования
и проводить сначала линейную интерполяцию
по этим узлам, а затем постепенно
привлекать следующие узлы таким образом,
чтобы они возможно симметричнее
располагались относительно точки.
Полученные при этом поправки будут
незначительными.
Пусть узлы интерполирования определены на [a,b] равномерно и заданы значения интерполируемой в этих узлах функции.
