Тест №2.

1. Для приведенной формулой является…

1) ;

2) ;

3) ; 4). 2. Сколько различных функций алгебры логики отnпеременных?

1) n;

2) ;

3) ;

4) .

3. Задать функцию формулой

1	1	0
1	0	1
0	1	0
0	0	0

1) ;

2) ;

3) ;

4) .

4. Пусть задана система высказывательных переменных . Элементарными дизъюнкциями не являются:

1) x;

2) ;

3) ;

4) .

5. Пусть задана система высказывательных переменных . Выписать элементарные конъюнкции.

1) ;

2) ;

3);

4) .

6. Найти тождественно истинные элементарные дизъюнкции:

1) ;

2) ;

3) ;

4) .

7. Какая из элементарных конъюнкций является тождественно ложной:

1) ;

2) ;

3) ;

4) .

8. Привести формулу к КНФ.

1) ;

2) ;

3) ;

4) .

9. Привести формулу к ДНФ.

1) ;

2) ;

3) ;

4) .

10. Пусть задана система высказывательных переменных . Какая из формул является СКНФ:

1)

2)

3)

4)

11. Пусть задана система высказывательных переменных. Какая из формул является СДНФ:

1) ;

2) ;

3) ;

4) .

12. Построить СДНФ для Апо таблице истинности:

		А
1	1	0
0	1	1
1	0	0
0	0	1

1) ;

2) ;

3) ;

4) .

13. Путем равносильных преобразований привести к СКНФ формулу .

1) ;

2) ;

3) ;

4) .

14. Какой является формула

1) Тождественно истинной;

2) Тождественно ложной;

3) Выполнимой.

15. Выразить черези – .

1) ;

2) ;

3) ;

4) .

Лекция 3. Приложение алгебры высказываний к логико-математической практике. П. 3.1. Релейно-контактные схемы.

Релейно-контактные схемы (РКС) часто называют переключательными схемами, используются в технике автоматического управления.

Под переключаемой схемой понимают схематическое изображение некоторого устройства, состоящее из элементов:

1. переключателей, которые могут быть механическими устройствами, электромагнитное реле и т.д.;

2. соединяющих их проводников;

3. входовв схему ивыходовиз нее (клеммы, на которые подается электрическое напряжение). Они называютсяполюсами.

Через 1 обозначим такое состояние электрической цепи, при котором та проводит ток, через 0 – состояние, при котором она ток не проводит.

Рассмотрим зависимости между шинами соединения переключателей и состояниями цепи.

1) Соединим переключатели ипоследовательно.

Построим таблицу проводимости этой цепи:

1	1	1
1	0	0
0	1	0
0	0	0

Эта таблица совпадает с таблицей истинности логической функции конъюнкции.

Таким образом, последовательному соединению переключателей соответствует операция конъюнкциив том случае, что состояние такого участка цепи при определенных положениях переключателей можно узнать, подставив соответствующие значения в формулу.

2) Соединим теперь переключатели ипараллельно

Таблица проводимости:

x	y
1	1	1
0	1	1
1	0	1
0	0	0

Таблица проводимости этой цепи выглядит так же, как и таблица истинности логической операции дизъюнкции. Таким образом, параллельному соединению переключателей соответствует операция дизъюнкции .

Так как любая формула алгебры высказываний может быть записана в СДНФ или СКНФ, то ясно, что любой формуле можно поставить в соответствие некоторую РКС, а каждой РКС можно поставить в соответствие некоторую формулу алгебры высказываний.

Пример 1: Составить РКС для формулы .

Решение:

Упростим .

Тогда РКС:

Пример 2: Упростить РКС.

Составим по РКС формулу – при упрощении использовали закон поглощения, тогда РКС примет вид:

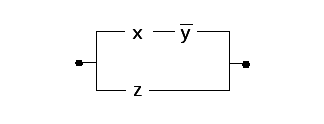
Пример 3: Построить схему, состоящую из трех переключателей, которые проводят ток только тогда, когда только один выключатель включен.

Решение: По данному условию работы схемы построим таблицу проводимости.

x	y	z
1	1	1	0
1	1	0	0
1	0	1	0
1	0	0	1
0	1	1	0
0	1	0	1
0	0	1	1
0	0	0	0

Построим формулу в виде СДНФ: . Тогда требуемая схема будет выглядеть следующим образом: