П.1.4. Равносильные формулы.

Определение 1.4.:Две формулыАиВ называются равносильными, если они принимают одинаковые логические значения при любом наборе значений входящих в формулу элементарных высказываний.

Равносильность обозначается знаком «». Для преобразования формул в равносильные важную роль играют основные равносильности, выражающие одни логические операции через другие, равносильности, выражающие основные законы алгебры логики.

Для любых формул А,В,Ссправедливы равносильности.

1. Основные равносильности

закон идемпотентности

1-истина

0-ложь

закон противоречия

закон исключенного третьего

закон поглощения

формулы расщепления

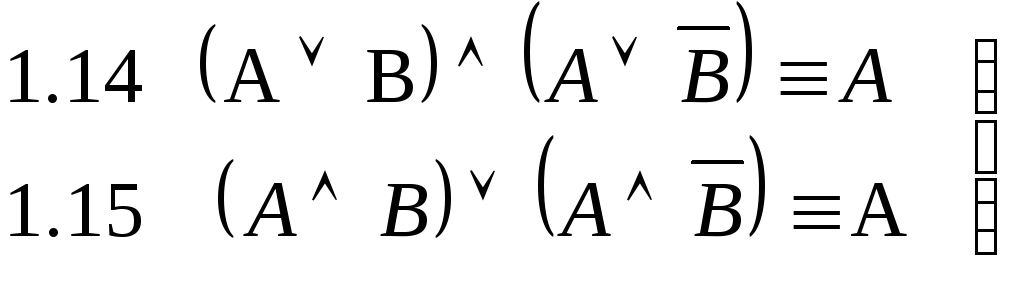закон склеивания

2. Равносильности, выражающие одни логические операции через другие.

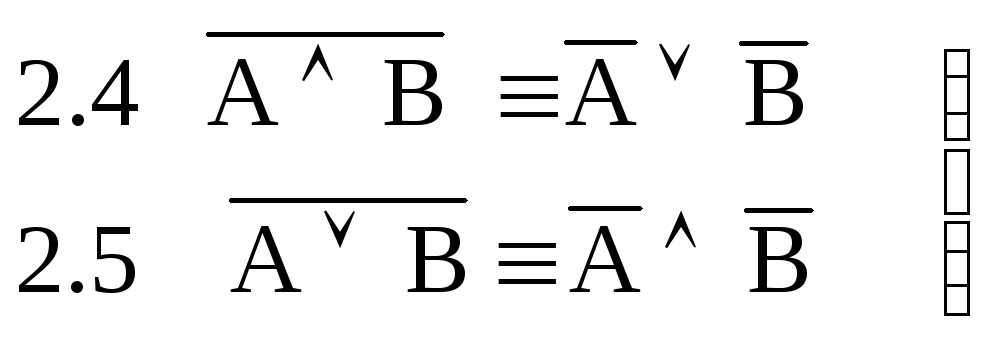закон де Моргана

3. Равносильности, выражающие основные законы алгебры логики.

коммутативный закон

ассоциативный закон

дистрибутивный закон

Любая из равносильностей легко может быть доказана с помощью таблицы истинности. Докажем первый закон де Моргана. Построим таблицу истинности для левой и правой части закона.

А 1	В 1	1	0	0	0	0
1	0	0	1	0	1	1
0	0	0	1	1	0	1
0	0	0	1	1	1	1

Если результирующие столбцы совпали, то формулы, стоящие в левой и правой части закона, равносильны.

Отношение равносильности есть отношение эквивалентности. Оно рефлексивно: симметрично, т.к. для любых двух формулАиВ: еслитранзитивно : еслиТаким образом, эквивалентные формулы можно рассматривать как разные формулы записи одной и той же формулы. Используя равносильностиI,II,IIIгрупп, можно формулу заменить равносильной ей формулой. Такие преобразования формул называются равносильными. Равносильные преобразования используются для доказательства равносильностей; для приведения формул к заданному виду, для упрощения формул.

Пример 14. Упростить формулу

При упрощении были использованы равносильности:

II (1), I (9), I (2), III (1), I (10).

Пример 15. Закон поглощения можно вывести при помощи равносильностей

I(3),III(5),I(4)

Вопросы и задания.

1. Среди следующих предложений выделите те, которые являются высказываниями, и установите, если это возможно, истинны они или ложны.

1) Число 2 является делителем числа 7.

2) На улице идет дождь.

3) Меню в программе – это список возможных вариантов.

4) Как пройти в библиотеку?

5) Математика – интересный предмет.

6) Москва – столица России.

7) «Да здравствуют музы!»

8) Студент МИКТ.

9) Алюминий тяжелее свинца.

2. Сформулируйте отрицание следующих высказываний, укажите значение истинности данных высказываний и их отрицаний.

1) Все простые числа нечетные.

2) 2>3.

3) Австралия – остров.

4) 12 есть составное число.

5) 2+2=4.

3. Определите значение истинности следующих высказываний:

1) Липецк расположен на берегу реки Воронеж и в нем проживает 100 тыс. человек.

2) 7 – простое число и 6 – составное число.

3) 7 – простое число или 6 – составное число.

4) Если 12 делится на 3, то 12 – составное число.

4. Даны два высказывания:

а: «число 5 является делителем 125»,

в: «число 5 – составное число».

В чем заключаются высказывания:

5. Определить, являются ли данная последовательность формулой:

1) ;

2) ;

3) ;

4) ;

5) .

6. Составить таблицы истинности для следующих формул и указать, какие из формул являются выполнимыми, какие – тождественно истинными, какие – тождественно ложными:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

7. Какие из следующих формул являются тавтологиями?

1) ;

2) ;

3) .

8. Какие из рассмотренных логических законов аналогичны законам алгебры чисел, а какие нет?

9. Доказать следующие равносильности:

1) ;

2) ;

3) .