Тема 5. Элементы математической статистики

Литература: , часть третья, гл. 15, параграфы 1-3, 6-8, гл. 16, параграфы 1 , 3-5, 9, 14-18, 20, гл.18, параграфы 1-4, 10-15, гл.19, параграфы 1-4, 22,, раздел 2, гл. 12, параграфы 8.1-8.3, 8.5, параграфы 12.1-12.8

Решение типовых задач

Пример 1:Отобрано 100 проб чернослива. Определили содержание углеводов в этих пробах. Результаты поместили в таблицу:

Таблица 6

50,2	54,0	41,0	42,0	58,2	59,3	84,8	45,0	76,5	58,3
21,0	55,0	45,0	21,5	46,0	44,0	42,5	49,0	48,7	75,0
15,3	55,0	23,8	46,5	53,0	62,8	78,5	67,0	34,5	49,9
49,7	63,0	30,0	32,0	42,4	22,4	52,0	70,4	57,2	50,0
23,0	47,8	47,4	50,8	78,3	27,0	56,6	51,3	58,6	28,4
51,7	50,0	48,8	49,4	57,5	47,4	33,5	27,0	39,7	57,5
18,4	35,6	28,4	37,6	49,5	26,7	54,0	68,6	29,3	62,7
43,8	44,0	69,1	46,3	76,7	37,1	69,2	39,3	30,0	43,0
85,0	63,0	30,0	43,8	64,8	22,0	38,8	42,3	64,8	41,0
30,0	10,0	63,0	48,8	71,2	54,4	47,8	31,2	46,1	17,8

Требуется определить закон распределения содержания углеводов в черносливе; найти точечные статистические оценки математического ожидания; дисперсии и среднего квадратичного отклонения.

Решение: Мы могли бы построить вариационный ряд содержания углеводов в черносливе. Для этого нужно упорядочить результаты по возрастанию, указав частоту встречаемости каждого из них.

Таблица 7

	10,0	15,3	17,8	…	85,0
	1	1	1	…	1

Значения вариант в таблице почти не повторяются. Поэтому построим интервальное распределение значений .Найдем минимальное и максимальное значение содержания углеводов в черносливе и. Найдем размах значений содержания углеводов в черносливе

Определим длину частичного интервала (классового интервала). Мы будем использовать формула Стэрджеса:

где - объем выборки. Определяем границы частичных интервалов. Нижняя граница первого интервала принимается, верхняя граница. Второй интервал, третий интервали так далее, пока не будет выполнено условие, где- верхняя граница последнего интервала ().

Замечание: Если какое-либо значение совпало с границей двух соседних интервалов, то его относят к левому интервалу (по договоренности).

Получаем следующее интервальное распределение содержания углеводов в черносливе:

Таблица 8

	1	9	14	19	29	15	7	6
	0,01	0,09	0,14	0,19	0,29	0,15	0,07	0,06

В таблице - частоты,- относительные частоты содержания углеводов в черносливе.

Замечание: Нужно проверить, что сумма частот , где- объем выборки, и сумма относительных частот.

Напомним, что распределение непрерывной случайной величины характеризуется функцией распределения плотности вероятностей (дифференциальным законом распределения).

В статистике ее оценкой служит гистограмма относительных частот. Гистограмма дает нам графическое представление количественной информации в виде столбиковой диаграммы. Высота столбцов пропорциональна количеству значений случайной величины (частоте), попавших на соответствующий интервал. Основаниями столбцов служат частичные интервалы, высоты определяются по формуле (плотности относительных частот). Для нашего примера:

Таблица 9

	1	9	14	19	29	15	7	6
	0,01	0,09	0,14	0,19	0,29	0,15	0,07	0,06
	0,001	0,009	0,014	0,019	0,029	0,015	0,007	0,006

Гистограмма относительных частот имеет вид:

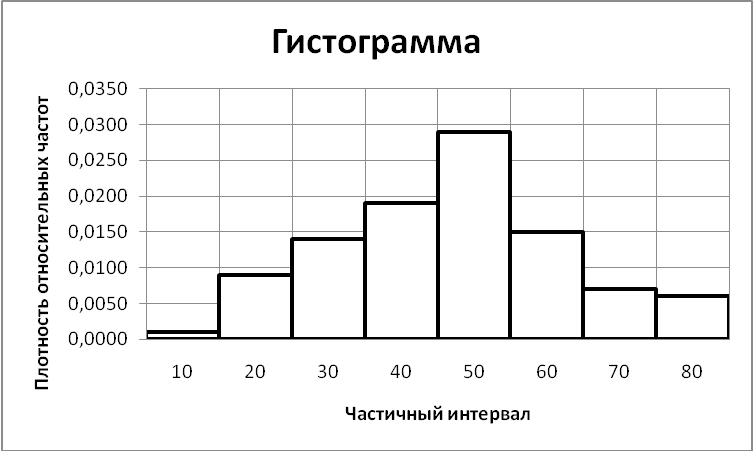
Рис. 5. Гистограмма

От интервальных распределения содержания углеводов в черносливе можно перейти к дискретному (точечному) распределению, взяв в качестве выборочных значений исследуемого признака середины частичных интервалов.

В нашем примере, дискретное распределение имеет вид:

Таблица 10

	10	20	30	40	50	60	70	80
	1	9	14	19	29	15	7	6
	0,01	0,09	0,14	0,19	0,29	0,15	0,07	0,06

Для наглядности построим полигон относительных частот. Вершины этой ломаной линии находятся в точках . Полигон относительных частот имеет вид:

Рис. 6. Полигон

По горизонтальной оси мы отложили середины частичных интервалов , по вертикальной оси отложены относительные частоты выборочных значений .

Для точечного распределения выборки можно построить эмпирическую функцию распределения . Эмпирическая функция распределения является статистической оценкой функции распределения вероятностей признака (интегрального закона распределения) и находится по формуле:

где - объем выборки,- сумма частот выборочных значений признака, которые меньше. Для нашего примера, получаем:

Заметим, что аналогом эмпирической функции распределения является кумулятивная кривая. Она для точечного (дискретного) выборочного распределения представляет собой ломаную линию с вершинами в точках , где - объем выборки,- сумма частот выборочных значений признака, которые меньше. Эмпирическая функция распределения икумулятивная кривая относительных частот служат характеристиками процесса накопления частот в рассматриваемой выборке.

Для нашего примера, кумулятивная кривая накопленных частот имеет вид:

Рис. 7. Кумулятивная кривая

Важнейшими характеристиками случайной величины являютсяматематическое ожидание , дисперсия исреднее квадратичное отклонение .

Точечными статистическими оценками этих параметров служат выборочное среднее , выборочная дисперсия, исправленная выборочная дисперсия, выборочное среднее квадратичное отклонение и исправленное среднее квадратичное отклонение.

Они вычисляются по формулам:

Выборочное среднее:

Выборочная дисперсия:

Исправленная выборочная дисперсия:

Выборочное среднее квадратичное отклонение:

Исправленное среднее квадратичное отклонение:

где - выборочное значение изучаемого признака,- частоты выборочных значений,- объем выборки.

Вычислим точечные статистические оценки параметров распределения признака .

Самостоятельно: Перед праздником 8 Марта опросили шестьдесят представителей сильного пола на тему: «Сколько подарков они собираются покупать?». Получили следующие результаты:

Таблица 11

3	2	5	6	6	1	4	6	4	6
3	6	4	2	1	5	3	1	6	4
5	4	2	2	4	2	6	3	1	5
6	1	6	6	4	2	5	4	3	6
4	1	5	6	3	2	4	4	5	2
5	6	2	3	5	4	1	2	5	3

Требуется определить закон распределения числа подарков; найти точечные статистические оценки математического ожидания; дисперсии и среднего квадратичного отклонения.

Ответ:

Таблица 12

	1	2	3	4	5	6
	7	10	8	12	10	13
	7/60	10/60	8/60	12/60	10/60	13/60

Таблица 13

Интер-вал
	7	10	8	12	10	13

Точечными статистическими оценками будут выборочное среднее , выборочная дисперсия, исправленная выборочная дисперсия, выборочное среднее квадратичное отклонение и исправленное среднее квадратичное отклонение.

Пример 2: В таблице представлены результаты выборочного измерения значений признака (первая строка) и значений признака(вторая строка).

Таблица 14

	21	50,2	15,3	49,7	23	51,7	18,4	43,8	85	30
	55	54	55	63	47,8	50	35,6	44,0	63	10

Требуется оценить тесноту линейной корреляционной связи между признаками и, и составить выборочное уравнение прямой регрессиина.

Решение:

Выпишем формулу для вычисления выборочного коэффициента корреляции:

где ,- выборочные средние и,- выборочные средние квадратичные отклонения признакови.

В нашем случае, выборочные средние: и. Выборочные средние квадратичные отклоненияи. Находим.

Выписываем выборочный коэффициент корреляции:

.

На практике приняты следующие пределы качественной характеристики тесноты связи:

1. - связь между иотсутствует или не является линейной;

2. - связь слабая;

3. - связь средней тесноты;

4. - связь тесная;

5. - связь очень тесная;

6. - связь между переменными исчитается функциональной.

Заметим, что данные, с помощью которых мы вычисляли, и будем строить уравнение связи между переменнымии, носят случайный характер. Проверить связь на случайность можно с помощью корреляционной поправки:

где ,- объем выборки (т.е. количество пар).

В нашем случае: .

Считается, что связь между переменными исущественная, если

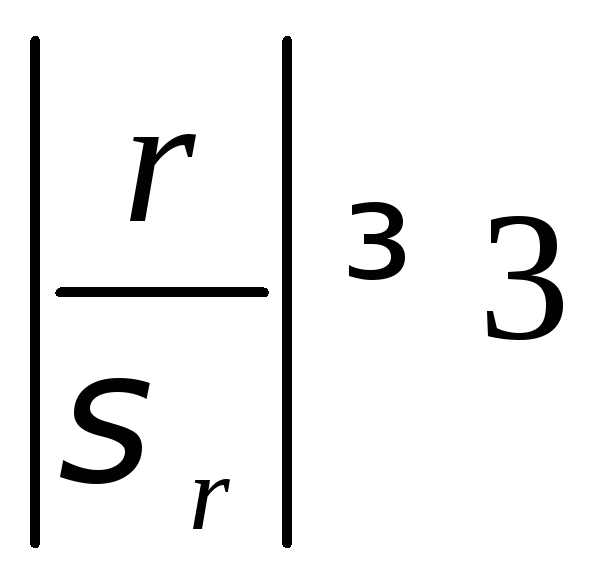
В нашем случае, , мы получили связь средней тесноты. Установим, является ли связь существенной. Получаем, что. Связь между переменнымиине является существенной.

Составим выборочное уравнение прямой регрессии на. Применяем формулу для не сгруппированных данных:

Подставляем наши данные:.

Получаем, что выборочное уравнение прямой регрессии имеет вид:.

Самостоятельно: В таблице представлены результаты выборочного измерения значений признака (первая строка) и значений признака(вторая строка).

Таблица 15

	0	1	2	3	4	5
	5,1	4,7	4,4	4,5	4,3	4,0

Требуется оценить тесноту линейной корреляционной связи между признаками и, и составить выборочное уравнение прямой регрессиина.

Ответ:.

Пример 3: Даны среднее квадратичное отклонение , выборочная средняяи объем выборкинормально распределенного признака генеральной совокупности. Найти доверительные интервалы для оценки генеральной среднейс надежностью.

Решение: Доверительный интервал (в котором с вероятностью будет находиться средняя генеральной совокупности) для нормально распределенной случайной величины с известным квадратичным отклонением , выборочной среднейи объемом выборкиравен

где - точность оценки, - значение аргумента, при котором функция Лапласа , где - надежность интервальной оценки. Значение функции Лапласа можно найти в Приложении 2.

В нашем случае, . По таблице Приложения 2 найдем значение аргумента, при котором функция Лапласа . По таблице при аргументе . Получаем доверительный интервал .

Вычисляем . В этом интервале с вероятность будет находиться средняя генеральной совокупности.

Самостоятельно: Даны среднее квадратичное отклонение , выборочная средняя и объем выборки нормально распределенного признака генеральной совокупности. Найти доверительные интервалы для оценки генеральной среднейс надежностью. Ответ:.

Пример 4: Дано исправленное среднее квадратичное отклонение ; выборочная средняяи объем выборкинормально распределенного признака генеральной совокупности. Найти, пользуясь распределением Стьюдента, доверительные интервалы для оценки генеральной среднейс надежностью.

Решение: Нам не известно генеральное среднее квадратичное отклонение. Интервальной оценкой генеральной средней нормально распределенного признака генеральной совокупности по величине выборочной средней при небольшом объеме выборки служит доверительный интервал:

где - надежность, - «исправленное» среднее квадратичное отклонение, - объем выборки. Значение находится в Приложения 3 по заданным значениям и .

В нашем случае, найдем в Приложении 3 по значениям и . Получаем . Подставляем , , и в формулу: .

Получаем: . В этом интервале с вероятностью будет находиться средняя генеральной совокупности.

Самостоятельно: Дано исправленное среднее квадратичное отклонение ; выборочная средняя и объем выборки нормально распределенного признака генеральной совокупности. Найти, пользуясь распределением Стьюдента, доверительные интервалы для оценки генеральной среднейс надежностью .

Ответ:.

Пример 5: При уровне значимости проверьте гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

Таблица 16

Эмпирические частоты,	6	12	16	40	13	8	5
Теоретические частоты,	4	11	15	45	13	6	6

Решение: Будем использовать критерий согласия(Пирсона). Найдем эмпирическое значение критерия:

В нашем случае,

Мы получили, . По таблицеПриложения 4 находим при уровне значимости и числе степеней свободы, где- число различных вариант выборки. Получаем. Так как, то у нас нет оснований отвергать гипотезу о нормальном распределении.

Самостоятельно: При уровне значимости проверьте гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:

Таблица 17

Эмпирические частоты,	14	18	32	70	20	36	10
Теоретические частоты,	10	24	34	80	18	22	12

Ответ:гипотеза о нормальном распределении генеральной совокупности отвергается.

Вопросы для проверки:

1. Укажите основные задачи математической статистики.

2. Что называют выборочной совокупностью? Что называют генеральной совокупностью?

3. Какие способы отбора объектов существуют?

4. Что называют статистическим распределением выборки?

5. Каким образом строят полигон и гистограмму?

6. Каким требованиям должны удовлетворять статистические оценки?

7. Выпишите формулы для вычисления генеральной и выборочной средней, генеральной и выборочной дисперсии.

8. Каким образом определяется мода, медиана, среднее абсолютное отклонение, коэффициент вариации вариационного ряда?

9. Какие зависимости являются функциональными, статистическими, корреляционными зависимостями?