Тема 4 случайные величины и их числовые характеристики. Основные законы распределения дискретных и непрерывных случайных величин.

Литература: , часть вторая, гл.6, параграфы 1-8, гл.7, параграфы 1-5, гл.8, параграфы 1-10, гл.10, параграфы 1-3, гл.11, параграфы 1-6, гл.12, параграфы 1-7, 9, гл.13, параграфы 1-3,, раздел 3, гл.3 , параграфы 3.1-3.7, гл.4, параграфы 4.1-4.8

Решение типовых задач:

Пример 1: Дан закон распределения дискретной случайной величины :

Таблица 1

Х	4,0	4,1	4,2	4,4
Р	0,1	0,2	0,3	0,4

Построить многоугольник распределения. Найти математическое ожидание случайной величины , дисперсию случайной величины, среднее квадратичное отклонение. Задать таблицей интегральную функцию распределения и построить ее график.

Решение:

Ряд распределения (закон распределения) случайной величины можно задать графически, откладывая по горизонтальной оси значения случайной величины, а на вертикальной оси – соответствующие им значения вероятностей. Графическое представление ряда распределения называетсямногоугольником распределения (Рис. 1):

Рис. 1. Многоугольник распределения

Математическое ожидание дискретной случайной величины, принимающей значенияс вероятностяминаходится по формуле:

В нашем случае:

.

Дисперсией называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть для дискретной случайной величины:

При вычислении дисперсии можно использовать следующее свойство дисперсии: дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата математического ожидания случайной величины.

В нашем случае:

.

Среднее квадратичное отклонениеравно квадратному корню дисперсии:

В нашем случае:

.

Для дискретной случайной величины вводится понятие интегральной функции распределения , которая равна вероятности случайного события состоящего в том, что дискретная случайная величинапримет одно из возможных значений, меньших некоторого, то есть

Если дискретные значения случайной величины расположены в порядке возрастания, то интегральную функцию распределения можно представить в виде:

Таблица 2

					1

В нашем случае:

Таблица 3

Функцию распределения можно представить в виде ступенчатой функции (Рис.2):

Рис. 2. Интегральная функция распределения

Самостоятельно: Дан закон распределения дискретной случайной величины :

Таблица 4

Х	40	41	42	44
Р	0,1	0,2	0,3	0,4

Построить многоугольник распределения. Найти математическое ожидание случайной величины , дисперсию случайной величины , среднее квадратичное отклонение. Задать таблицей интегральную функцию распределения и построить ее график.

Ответ:

Таблица 5

Пример 2: Непрерывная случайная величина заданаинтегральной функцией распределения:

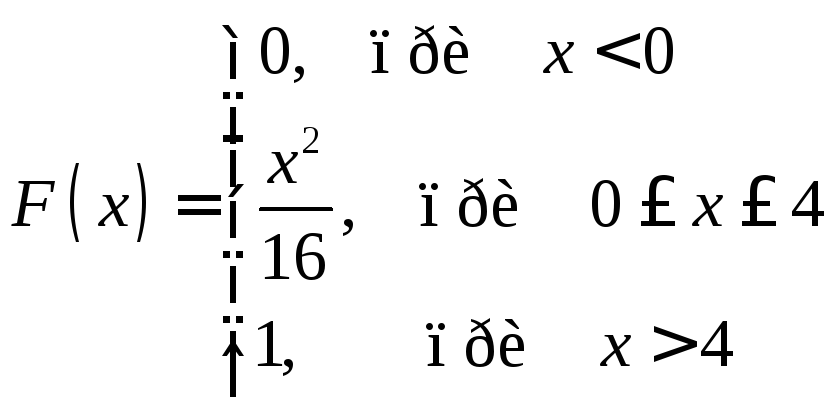
Построить график интегральной функции распределения. Найти дифференциальную функцию распределения. Построить график дифференциальной функции распределения. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.

Решение: График интегральной функции распределения:

Рис. 3. Интегральная функция распределения

Дифференциальная функция распределения имеет вид:

Построим график интегральной функции распределения:

Рис.4. Дифференциальная функция распределения

Найдем математическое ожидание непрерывной случайной величины:

В нашем случае:

Дисперсию непрерывной случайной величины можно вычислить по формулам:

Вычислим дисперсию по второй формуле:

Найдем среднее квадратичное отклонение:

.

Самостоятельно: Непрерывная случайная величина задана интегральной функцией распределения:

Построить график интегральной функции распределения. Найти дифференциальную функцию распределения. Построить график дифференциальной функции распределения. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.

Ответ:

Пример 3:Математическое ожидание нормально распределенной случайной величины – количество тертого грецкого ореха, используемого для приготовления четырех порций салата «Южный» с орехами, равно 40 грамм, со среднеквадратичным отклонением 3 грамма.

Найти вероятность того, что четыре порции салата будут содержать не менее тридцати четырех грамм и не более сорока трех грамм грецкого ореха; вероятность того, что количество грецкого ореха отклонится от его математического ожидание не более чем на 1,5 грамма.

Решение: Пусть – количество грецкого ореха в салате. Напомним, что если случайная величина распределена по нормальному закону, то вероятность попадания случайной величины в интервал вычисляется по формуле:

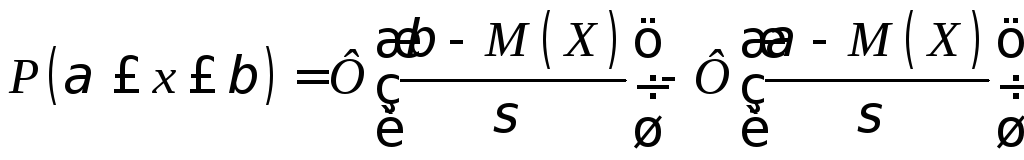
где – функция Лапласа (Приложение 2), где– математическое ожидание,– среднее квадратичное отклонение.

В нашем случае вероятность того, что четыре порции салата будут содержать не менее тридцати четырех грамм и не более сорока трех грамм грецкого ореха, вычисляется:

Напомним, что , то есть функция Лапласа нечетная.

Найдем вероятность того, что количество грецкого ореха отклонится от его математического ожидание не более чем на 1,5 грамма. Эта вероятность является вероятностью того, что количество грецких орехов попадет в интервал.

Вычислим эту вероятность:

Самостоятельно: Срок безотказной работы телевизора представляет собой нормально распределенную случайную величину с математическим ожиданием 12 лет и средним квадратичным отклонением 3 года. Найти вероятность того, что телевизор проработает от 6 до 9 лет. Найти вероятность того, что срок безотказной работы телевизора отклонится от математического ожидания не более чем на 3 года.

Ответ: .

Вопросы для проверки:

1. Какая величина называется случайной?

2. Какая случайная величина называется дискретной? Какая случайная величина называется непрерывной?

3. Какое соответствие называется законом распределения дискретной случайной величины?

4. Какая функция называется интегральной функцией распределения? Перечислите ее основные свойства.

5. Какая функция называется дифференциальной функцией распределения (плотностью распределения)? Перечислите ее основные свойства.

6. Каким образом вычисляется математическое ожидание, дисперсия и среднее квадратичное отклонение дискретной случайной величины и непрерывной случайной величины?

7. В чем состоит вероятностный смысл математического ожидания?