
курс лекции по начерательной геометрии
.pdf
51
Л Е К Ц И Я 6
ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА ВРАЩЕНИЕМ ОРИГИНАЛА ВОКРУГ ОСИ
6.1. Общие замечания
Как уже отмечалось, целью любого преобразования КЧ является получение новых изображений (проекций) ГО.
При задании новой ПП эта плоскость является носителем новой проекции ГО, который при этом остается неподвижным (см. лекцию 1). При вращении ГО вокруг неподвижной оси он перемещается относительно Ï1 и Ï2 до тех пор, пока интересующий нас элемент ГО не займет нужное нам частное относительно них положение, после чего ГО проецируется на Ï1 и Ï2. Таким образом, при вращении ГО каждая из ПП Ï1 и Ï2 будет являться носителем двух полей проекций - старых и новых.
|
j |
|
|
|
|
При вращении (повороте) в |
|
|
том или ином направлении ГО |
||||||
m |
|
||||||
|
вокруг оси j его точки М |
вра- |
|||||
|
|
||||||
M |
|
щаются вокруг j по окружностям |
|||||
|
m |
|
|
|
до занятия этими точками |
||
O |
|
|
|
|
|||
|
|
|
|||||
|
|
требуемого положения М |
(рис. |
||||
M |
|
6.1). Плоскости окружностей m |
|||||
|
перпендикулярны оси |
j, их |
|||||
|
|
центры O находятся на оси j. |
|||||
Рис. 6.1
Договоримся над обозначением
повернутого ГО наносить черту, а при вращении вокруг двух осей - две черты.
Точки ГО, расположенные на оси j, при вращении неподвижны. В общем случае для поворота прямой достаточно повернуть две её точки, а для поворота плоскости - три её точки.
6.2. Способ вращения оригинала вокруг проецирующей оси
Суть способа вращения вокруг проецирующей оси: ГО поворачивают вокруг оси j, перпендикулярной к Ï1 или Ï2, до тех пор, пока ГО не займет нужного положения относительно Ï2 или Ï1. При вращении ГО проекции его точек на плоскости проекций, перпендикулярной к оси вращения, перемещаются по концентрическим окружностям, а на другой плоскости проекций - по отрезкам,

|
|
|
52 |
|
|
|
перпендикулярным к проекции оси j. На |
M2 |
M2 |
||||
рис. 6.2 ось j Ï1, траектория перемеще- |
||||||
O2 |
m2 |
|||||
ния проекции M2 - отрезок m2 |
j2, проек- |
|||||
j2 |
|
|||||
ции M1 - окружность m1 , причем радиус õ |
|
|
||||
вращения точки M и угол её поворота f, |
|
m1 |
||||
проецируются на Ï1 |
в |
натуральную |
|
|
||
величину ( 1O,M1 = 1 O1 |
,M1 1 |
; |
1 f1 =f1 ). |
O1 j1 |
|
|
Поэтому при вращении ГО его проекция |
|
|
||||
на ПП, к которой |
ось |
|
вращения |
1 |
|
|
перпендикулярна, меняет только свое |
M1 |
M1 |
||||
положение, не меняя формы и |
|
|
||||
размеров. |
|
|
|
Рис. 6.2 |
|
|
ПРИМЕР 6.1. Вращением вокруг проецирующей оси перевести прямую t (t1 ,t2 ) общего положения в положение горизонтали.
При решении 1ОЗПЧ для перевода прямой в положение горизонтали прямую вращают вокруг оси j Ï2, для перевода в положение фронтали - вокруг оси j
Ï2, для перевода в положение фронтали - вокруг оси j  Ï1 .
Ï1 .
Чтобы перевести прямую t в положение горизонтали (рис. 6.3), возьмем на t две точки A, B и зададим проходящую через точку B
ось j |
Ï2 : |
j1 |
B1 |
|
j1 |
x1 |
2 ; j2 |
B 2 . |
При вращении точка |
|||
B |
j будет неподвижна (B |
B |
B1 |
B1 |
B2 B2 |
), поэтому для |
||||||
поворота t |
достаточно |
повернуть |
точку |
A. |
Так |
как прямая t |
||||||
|
|
t2 |
A2 |
|
|
|
|
|
|
|
j2 |
|
|
|
m2 |
|
|
|
|
h2 m2 |
|
|
B2 B2 A2 h2 |
||
|
|
|
|
|
|
|
|
|
A2 |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
t2 |
A2 |
|
|
B2 |
j2 B2 |
|
|
|
|
||
x1 |
2 |
|
|
|
|
|
|
x1 |
2 |
|
m1 |
h1 |
|
|
|
|
|
B1 |
B1 |
|
|
|
|||
|
|
|
|
|
|
h1 |
|
|
||||
|
|
|
|
|
|
|
|
A |
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
A |
|
m1 |
|
|
|
|
|
A1 |
B1 j1 B1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
A1 |
|
|
|
|
|
|
|
|
|
t1 |
t1 |
|
j1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.3 |
Рис. 6.4 |

53
должна занять положение t 
 Ï1, проведем через B2 проекцию t2
Ï1, проведем через B2 проекцию t2 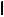


 x1
x1 2 и найдем A2=m2
2 и найдем A2=m2  t2, где m 2 - дуга, по которой двигается проекция A2 точки A. Проекция A1 перемещается по отрезку m1: m1
t2, где m 2 - дуга, по которой двигается проекция A2 точки A. Проекция A1 перемещается по отрезку m1: m1 B1
B1 
 m1
m1 
 x1
x1 2. Проекцию A1 повернутой точки A определим на отрезке m1 с помощью проведенной из A2 линии связи. Проекция t1 повер- нутой прямой t
2. Проекцию A1 повернутой точки A определим на отрезке m1 с помощью проведенной из A2 линии связи. Проекция t1 повер- нутой прямой t 
 Ï1 пройдет через точки B1 и A1. Заметим, что
Ï1 пройдет через точки B1 и A1. Заметим, что  A1,B1
A1,B1 - длина отрезка [A,B].
- длина отрезка [A,B].
На рис. 6.4 решена 2ОЗПЧ: горизонталь h переведена в поло- жение фронтально проецирующей прямой h  Ï2. Для этого на h взяли точки A, B и задали ось j, проходящую через точку B перпендику-
Ï2. Для этого на h взяли точки A, B и задали ось j, проходящую через точку B перпендику-
лярно к Ï1 : j1 B1; j2 |
B2 |
j2 |
x1 |
2; B1 B1 ; B2 |
B2. |
При h |
Ï2 |
в поле Ï1 проекция h1 |
B1 |
h1 |
x1 |
2, точка A1=m1 |
h1. |
В поле |
Ï2 |
проекция A2 ищется на m2  j2 с помощью линии связи, проведенной
j2 с помощью линии связи, проведенной
из A1 . Поэтому A2 |
|
B2 |
|
h2. |
|
|
На |
|
рис. |
6.5 |
прямая t |
||||||
|
|
t |
A |
2 |
A |
2 |
B2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
B2 j12 |
|
2 |
|
|
|
|
общего |
положения |
вращением |
||||||||
B2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
вокруг |
проецирующих осей |
||||||||||
|
|
|
|
|
t2 |
|
|
|
переведена |
в |
проецирующее |
||||||
|
|
|
|
|
|
|
|
положение t |
|
Ï2. Для поворота |
|||||||
A2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
j22 |
прямой t на ней взяли точки A, B |
|||||||||
t2 |
|
|
|
|
|
|
|
и |
последовательно |
вращали t |
|||||||
|
|
|
|
|
|
|
B1 |
вокруг двух проецирующих осей. |
|||||||||
|
|
|
|
|
|
|
|
Сначала задали ось j1 |
B j1 Ï2 |
||||||||
|
|
|
|
|
|
|
|
|
и вращением вокруг j1 |
перевели |
|||||||
B |
B |
|
|
|
|
|
|
|
в положение t Ï1. Затем задали |
||||||||
1 |
|
1 |
|
|
|
t1 |
|
t |
ось j |
2 |
A |
j |
2 |
Ï1 |
и повернули |
||
t1 |
|
|
|
|
|
|
|
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
прямую t |
Ï1 в положение t Ï2. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
На рис.6.6 плоскость об- |
||||||
A1 |
j11 |
|
A |
j2 |
A |
|
щего положения S( ABD) враще- |
||||||||||
|
1 |
нием вокруг проецирующей оси j |
|||||||||||||||
|
|
|
|
1 |
1 |
|
|||||||||||
|
Рис. 6.5 |
|
|
|
|
( j |
|
D |
|
j |
Ï1 ) переведена в |
||||||
|
|
|
|
|
положение S |
|
Ï2 . Точка D при |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
вращении неподвижна (D D), поэтому поворот плоскости S сводится |
|||||||||||||||||
к повороту двух её точек A и B.
Так как у фронтально проецирующей плоскости горизонталь h  Ï2 , то через точку D в S провели горизонталь h и повернули её
Ï2 , то через точку D в S провели горизонталь h и повернули её

|
|
54 |
|
|
||
вокруг оси j до положения h Ï |
2 |
B2 |
j2 |
B2 |
||
(h2 D2, h |
D1 h1 x1 2). |
m1 |
||||
|
S2 |
|
||||
Для |
поворота плоскости S |
|
|
|||
использовали точку E=h 
 [A,B].
[A,B].
E1 =m1
 h1 и E2
h1 и E2 D2
D2 h2 - её проек-
h2 - её проек-
ции в повернутом положении.
Поскольку j |
Ï1 , то |
D1B1E1 = |
= D1B1 E1 . |
Точку B1 |
строили из |
условия равенства этих треугольников ( D1 B1 E1 строился по трем
D1 B1 E1 строился по трем
сторонам). Затем |
на прямой |
(B1,E1) от точки E1 отложили отре- |
|
зок [E1 ,A1 ] ( E1 ,A1 |
= E1 ,A1 ) и |
h2 |
D2 D2 h2 E2 E2 |
A2 |
A2 |
õ1 2 |
|
D1 |
j1 D1 |
|
h1 |
|
A1 |
нашли проекцию A1 . Точка B2 |
h1 |
|
|
|||
есть точка пересечения |
линии |
|
E1 |
|||
связи, |
проведенной из |
B1 |
, и |
|
|
|
перпендикуляра к j2 из точки |
B2. |
|
|
B1 |
||
На S2 |
B2,D2 находится проек- B1 |
E1 |
A1 |
m1 |
||
ция A2. |
|
|
|
|
Рис. 6.6 |
|
6.3. Способ вращения оригинала вокруг линии уровня
Способ вращения ГО вокруг линии уровня целесообразно применять для определения натурального вида плоской фигуры, лежащей в плоскости общего положения, путем перевода её в положение плоскости уровня.
Так, вращая плоскость общего положения вокруг её горизонтали h, плоскость можно перевести в горизонтальное положение, при котором фигуры, расположенные в этой плоскости, на Ï1 проецируются в натуральную величину, а на Ï2 - в отрезки, параллельные оси проекций x1 2. Точки вращаемой вокруг горизонтали фигуры перемещаются по окружностям, плоскости которых перпендикулярны к горизонтали и к Ï1. Поэтому горизонтальные проекции точек вращаемой фигуры перемещаются по отрезкам, перпендикулярным проекции h1 горизонтали.
2. Точки вращаемой вокруг горизонтали фигуры перемещаются по окружностям, плоскости которых перпендикулярны к горизонтали и к Ï1. Поэтому горизонтальные проекции точек вращаемой фигуры перемещаются по отрезкам, перпендикулярным проекции h1 горизонтали.
ПРИМЕР 6.2. Используя вращение вокруг линии уровня, найти величину угла между пересекающимися прямыми a и b (рис. 6.7).
Прямые a и b задают плоскость общего положения S(a 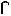
 b).
b).

|
|
|
|
|
|
|
55 |
|
|
|
|
|
|
|
|
|
Построим её горизонталь h и получим |
ABD, угол при вершине B |
|||||||||||||||
которого |
является |
искомым. Решение примера сводится к |
||||||||||||||
определению натурального вида этого треугольника. |
|
|
|
|
|
|||||||||||
|
При повороте плоскости S вокруг горизонтали h до положения |
|||||||||||||||
S |
Ï1 |
горизонталь h остается неподвижной: h |
h; |
A |
A; |
D |
|
D. |
||||||||
Поэтому для поворота плоскости S достаточно повернуть её точку B. |
||||||||||||||||
Зададим плоскость DB, в которой вращается точка B. Так как DB |
h, |
|||||||||||||||
то DB |
Ï1 |
и DB задаётся своей основной проекцией DB1 |
B1 |
DB1 |
|
h1. |
||||||||||
|
|
|
|
B2 |
|
|
|
|
|
Найдем |
центр |
враще- |
||||
|
|
|
|
|
|
|
|
ния точки B точку O: O=h |
DB и |
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
s |
|
|
|
|
определим |
по |
правилу |
пря- |
||||
A2 |
|
|
h |
h |
S2 |
моугольного |
треугольника |
|||||||||
|
|
|
||||||||||||||
a2 |
|
|
O2 |
|
D2 |
2 |
2 |
|
величину радиуса |
вращения |
||||||
|
|
|
b2 |
|
|
B,O точки B. Один катет этого |
||||||||||
x1 2 |
|
|
B1 |
|
|
|
|
|
треугольника - отрезок [B1 ,O1 ], |
|||||||
|
|
|
b1 |
|
|
|
|
а второй, отмеченный знаком |
||||||||
|
|
|
|
|
|
|
|
“s”, брался в поле Ï2. |
|
|
|
|||||
a1 |
|
|
|
b1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
Плоскость S займет по- |
||||||||||
a1 |
|
|
O1 |
|
|
h1 |
h1 |
ложение S |
Ï1, когда |
радиус |
||||||
|
|
|
D1 |
D1 |
|
|
вращения |
точки |
B |
будет |
||||||
|
|
|
|
|
|
|||||||||||
A1 |
A1 |
|
|
|
|
|
|
|
проецироваться на Ï1 |
в |
нату- |
|||||
|
|
|
|
DB1 |
|
|
ральную величину и проекция |
|||||||||
|
|
|
|
B1 |
B1 |
будет удалена от h 1 |
h1 |
на рас- |
||||||||
|
|
|
|
B |
стояние |
|
B1 ,O1 |
= B1 ,O1 . |
Построенный |
|||||||
|
|
B,O |
D1 |
A1 B1 D1 |
|
соответствует |
натуральному |
|||||||||
|
|
|
Рис. 6.7 |
виду |
ABD, а величина угла при вершине |
|||||||||||
|
|
|
B1 - величине угла между прямыми |
a |
и |
b. |
||||||||||
6.4. Определение углов 6.4.1. Угол между пересекающимися прямыми
Угол между пересекающимися прямыми - плоская фигура, натуральный вид которой в общем случае ищут одним из трех способов:
-вращением вокруг линии уровня (см. ПРИМЕР 6.2);
-без преобразования КЧ (см. рис. 6.9.);
-способом задания новой ПП (см. ПРИМЕР 5.14).
6.4.2. Угол между прямой линией и плоскостью
Угол между прямой линией t и плоскостью S измеряется углом f между прямой t и её проекцией tS на плоскость S (рис. 6.8).

|
|
56 |
|
|
|
180 -d |
|
|
Для построения угла f надо |
||
|
M |
найти на плоскости S проекцию tS |
|||
|
прямой t, проходящую через точки |
||||
d |
|
||||
|
N=t |
S и K=l S (l - перпендикуляр к |
|||
|
|
||||
f |
tS |
плоскости S, проведенный через |
|||
|
Ê |
произвольную точку M |
t). Прямые |
||
N |
t и tS пересекаются в точке N под |
||||
|
|||||
|
|
углом f, который можно найти |
|||
t |
|
одним из способов |
определения |
||
l |
угла |
между пересекающимися |
|||
|
прямыми (см. раздел 6.4.1). |
||||
|
|
|
Если необходимо узнать толь- |
||
Рис.6.8 |
|
ко величину угла f, не строя сам |
|||
|
угол, |
то величину угла f обычно |
|||
|
|
||||
ищут в такой последовательности (рис. 6.8):
1.На прямой t берется произвольная точка M.
2.Через точку M проводят перпендикуляр l к плоскости S.
3.Ищут острый угол d между пересекающимися прямыми l и t.
4.Величину угла f находят из условия f=90 -d.
-d.
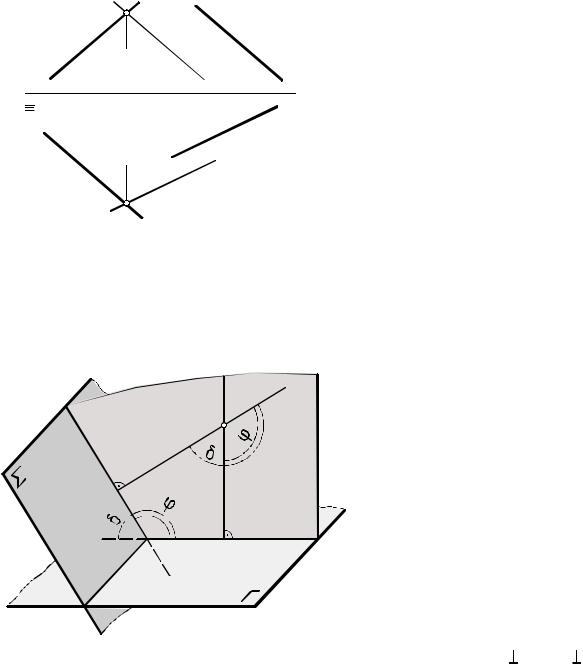
На рис. 6.9 и 6.10 ищется величина угла f между прямой t и плоскостью S(a  b). Для этого на обоих рисунках через произволь-
b). Для этого на обоих рисунках через произволь-
ную точку M |
t провели прямую l S (в плоскости S строили гори- |
зонталь h, |
фронталь f и проводили l1 h1 и l2 f2), определили |
угол d между прямыми t и l, а затем угол f=90 -d. В обоих случаях при определении величины угла d искали натуральный вид
-d. В обоих случаях при определении величины угла d искали натуральный вид  AMB, образованного при пересечении прямых l и t какой-то горизонталью
AMB, образованного при пересечении прямых l и t какой-то горизонталью
h1 |
Ã(l t). |
|
|
|
|
На рис. 6.9 треугольник |
AMB с углом |
d |
при вершине M |
построен по трем сторонам. |
Сторона [A,B] |
h1 |
и её длина A,B = |
|
= A1 ,B1 , длину A,M стороны [A,M] определили по правилу прямо- |
||||
угольного треугольника из A1 M1 F, а длину M,B |
стороны [M,B] - из |
|||
B1M1E. На рис. 6.10 натуральный вид AMB, как в ПРИМЕРЕ 6.2, |
||||
найден в результате вращения |
AMB вокруг горизонтали h1 : AMB = |
|||
= |
A1 M1B1 . На обоих рисунках f=90O-d. |
|
|
|

a2
a1
A
a2
a1
57
f2 |
l2 |
t2 |
b2 |
A2 |
h21 |
|
 B2
B2
h2
h1 |
M |
2 |
A1 |
|
|
|
|
|
|
|
l1 |
|
f1 |
|
b1 |
A,M |
|
M |
||
|
F
 B
B
Рис. 6.9
b2 f2
h2
h1
f1 l1
b1  M,O
M,O 
Рис. 6.10

 A,B
A,B
M1 |
B1 t |
|
1 |
 B,M
B,M h11
h11
 E
E
l2 t2
A2 O2 h12
 B2
B2
 M2
M2
A1 A1
A1
 M1
M1
|
О1 |
|
M1 |
t1 |
|
B1 h11 |
||
B1 |
58
6.4.3. Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми линиями (лекция 2) измеряется углом между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
|
M2 |
b2 |
Обычно при определении |
|
угла между скрещивающимися |
||
a2 |
|
|
|
l2 |
|
прямыми a и b (рис. 6.11) на |
|
x1 2 |
|
|
одной из них, например на a, |
|
b1 |
берут произвольную точку M, |
|
a1 |
|
проводят через M прямую l, |
|
l1 |
|
параллельную второй прямой |
|
|
|
(на рис. 6.11 прямой b), и |
|
|
M1 |
|
любым способом находят угол |
|
|
между пересекающимися пря- |
|
|
Рис. 6.11 |
|
мыми a и l, равный искомому. |
|
|
|
6.4.4. Угол между плоскостями
Две пересекающиеся плоскости S и Ã образуют четыре попарно равных двугранных угла. Двугранные углы между плос-
D |
t |
l |
костями измеряются линей- |
||
ными углами f и d между |
|||||
|
|
||||
M |
|
|
|||
|
|
прямыми d и g, по которым |
|||
d |
|
|
|||
|
|
|
плоскость D, перпендику- |
||
|
|
|
лярная к плоскостям S и G, |
||
|
g |
|
пересекает эти |
плоскости |
|
|
|
(рис. 6.12). |
|
||
e |
|
|
Обычно, если линия e |
||
|
|
пересечения плоскостей S и |
|||
Рис. 6.12 |
|
|
G неизвестна, для построе- |
||
|
|
ния углов f и d из произ- |
|||
вольной точки M пространства проводят перпендикуляры l |
S и t G, |
||||
углы между которыми равны искомым (рис. 6.12). На рис. 6.13 построены проекции перпендикуляров l и t, проведенных из некой точки M к плоскостям S(a 
 b) и G(A,B,D,A). Для определения величины углов f и d между плоскостями S и Gостается только одним из известных способов найти углы между пересекающимися прямыми l и t.
b) и G(A,B,D,A). Для определения величины углов f и d между плоскостями S и Gостается только одним из известных способов найти углы между пересекающимися прямыми l и t.

59
|
|
a2 |
b2 |
l2 |
|
t2 |
|
|
|
|
|
|
|
|
|
B2 |
|||
|
h2 |
|
|
|
1 |
|
|
||
|
|
|
|
|
f2 |
|
|
|
|
|
f2 |
|
|
M2 |
|
1 |
|
|
D2 |
|
|
|
l1 |
|
h2 |
|
|
||
|
|
|
|
t1 |
A2 |
|
|
|
|
|
|
|
|
|
A1 |
|
h11 |
||
|
|
|
|
|
|
|
|||
|
f1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
h1 |
|
b1 |
M1 |
|
f11 |
|
|
D1 |
|
a1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
B1 |
|
|
|
|
|
|
Рис. 6.13 |
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
42 |
|
Если |
известно |
ребро двугранного |
|||
|
|
b2 |
|||||||
|
|
угла (линия пересечения плоскостей, |
|||||||
|
12 |
h2 |
|
||||||
|
|
образующих угол), то величину угла |
|||||||
|
|
a2 |
32 |
удобно определять |
|
с |
использованием |
||
|
|
|
22 |
способа задания новых ПП, переводя |
|||||
x1 |
|
|
|
ребро угла в проецирующее положение. |
|||||
2 |
h1 |
31 |
На рис. 6.14 таким образом найден угол |
||||||
|
|
между плоскостями |
S(a |
h) и G(a b) с |
|||||
|
|
|
|||||||
|
|
a1 |
|
известным ребром |
a, а на рис. 6.15 - |
||||
|
11 |
21 угол между плоскостями треугольников |
|||||||
|
|
|
|||||||
|
|
41 |
b1 |
ABD и ABE с известным ребром ÀÂ. |
|||||
x1 |
3 |
|
|
|
|
|
|
|
|
|
|
a4 |
|
14 24 |
|
|
|
||
|
|
a3 |
|
|
|
|
|
||
|
|
23 |
|
|
|
S |
|
|
|
1 |
|
h3 |
à |
|
34 |
4 |
|
||
3 |
33 |
|
4 |
|
|
|
|
|
|
|
|
|
b4 44 |
|
|
|
|
|
|
|
43 |
b3 |
|
|
|
|
|
|
|
|
|
|
õ3 |
4 |
|
|
|
|
|
Рис. 6.14

60
D2
 A2
A2
E2
B2 |
E3 |
õ1 2
2
 A1
A1
E1
D1
B3
B1 õ1 3
3
Л Е К Ц И Я 7
ПОВЕРХНОСТИ
E4
 D4
D4
A4 B4
B4
 A3
A3
õ3 4
4
 D3
D3
Рис. 6.15
7.1.Образование поверхности
ВНГ поверхность обычно рассматривают как результат движения в пространстве линии, перемещающейся по какому-либо закону.
Линия, перемещающаяся в пространстве и образующая при этом поверхность, называется образующей поверхности, а закон её перемещения - законом образования поверхности.
На рис. 7.1 приведен пример образования конической поверхности общего вида. Эта поверхность может быть образована прямой
линией l (образующей), двигающейся по закону (li  k, li
k, li  T), согласно которому в любом i-м положении образующая li пересекает заданную линию k и проходит через заданную точку T (вершину).
T), согласно которому в любом i-м положении образующая li пересекает заданную линию k и проходит через заданную точку T (вершину).
Всё многообразие поверхностей определяется разнообразием форм образующих линий и законов образования поверхностей.
