
курс лекции по начерательной геометрии
.pdf
41
Л Е К Ц И Я 5
КОМПЛЕКСНЫЕ ПОЗИЦИОННО-МЕТРИЧЕСКИЕ ЗАДАЧИ 5.1. Общие замечания
Комплексные позиционно-метрические задачи составляют важнейший раздел курса, связанный с решением обратной задачи НГ. Эти задачи получили свое название в силу того, что для выполнения большинства из них необходимо последовательно решать определенные позиционные и метрические задачи.
Рассматриваемые комплексные задачи можно условно разбить на четыре группы, выделив в каждой группе ключевую задачу, на базе которой решаются остальные задачи группы. Сформулируем эти ключевые задачи:
1.Определение расстояния от точки до плоскости.
2.Определение расстояния от точки до прямой линии.
3.Определение расстояния между скрещивающимися прямыми.
4.Определение натурального вида треугольника. Комплексные позиционно-метрические задачи могут решаться без
преобразования КЧ с использованием основных метрических и главных позиционных задач или с преобразованием КЧ с использованием четырех ОЗПЧ и свойств прямых и плоскостей частного положения.
5.2. Определение расстояния от точки до плоскости
Расстояние от точки M до плоскости S равно длине отрезка  M,K
M,K перпендикуляра l, опущенного из точки на плоскость (рис. 5.1). Задача решается согласно ПА (не зависит от способа решения):
перпендикуляра l, опущенного из точки на плоскость (рис. 5.1). Задача решается согласно ПА (не зависит от способа решения):
1.Через точку M проводят перпендикуляр l к плоскости S -1ОМЗ.
2.Ищут точку K пересечения перпендикуляра l и плоскости S - 1ГПЗ.
3. Определяют длину отрезка  M,K
M,K перпендикуляра l - 2ОМЗ.
перпендикуляра l - 2ОМЗ.
l |
|
l |
l |
|
|
M |
|||
M |
a |
M |
||
|
||||
|
|
|
||
K |
|
K |
K |
|
Рис. 5.1 |
|
Рис. 5.2 |
Рис. 5.3 |
Рассматриваемая задача является ключевой для группы задач, в которую, в частности, входят задачи: определить расстояние между прямой и параллельной ей плоскостью; определить

42
расстояние между параллельными плоскостями; через точку плоскости провести к плоскости отрезок перпендикуляра заданной длины; построить плоскость, параллельную данной плоскости и удаленную от неё на указанное расстояние.
Расстояние от прямой a до параллельной ей плоскости S определяется длиной отрезка  M,K
M,K перпендикуляра l, опущенного из произвольной точки M прямой на плоскость (рис. 5.2). Поэтому, чтобы найти расстояние от прямой до параллельной ей плоскости, достаточно на прямой взять точку и найти расстояние от неё до плоскости, то есть решить ключевую задачу. Расстояние между параллельными плоскостями G и S измеряется длиной отрезка
перпендикуляра l, опущенного из произвольной точки M прямой на плоскость (рис. 5.2). Поэтому, чтобы найти расстояние от прямой до параллельной ей плоскости, достаточно на прямой взять точку и найти расстояние от неё до плоскости, то есть решить ключевую задачу. Расстояние между параллельными плоскостями G и S измеряется длиной отрезка  M,K
M,K перпендикуляра l, опущенного из произвольной точки M одной плоскости на другую (рис. 5.3). Следовательно, чтобы найти расстояние между параллельными плоскостями, достаточно в одной из плоскостей взять точку и найти расстояние от неё до второй плоскости, то есть опять же решить ключевую задачу.
перпендикуляра l, опущенного из произвольной точки M одной плоскости на другую (рис. 5.3). Следовательно, чтобы найти расстояние между параллельными плоскостями, достаточно в одной из плоскостей взять точку и найти расстояние от неё до второй плоскости, то есть опять же решить ключевую задачу.
ПРИМЕР 5.1. Заданы точка M(M1 ,M2) и плоскость S(A,a) (рис. 5.4). 
 M,S
M,S - найти расстояние от точки M до плоскости S без
- найти расстояние от точки M до плоскости S без
преобразования КЧ. |
|
|
|
|
Пояснения к решению: 1. l |
M |
l |
- |
через точку M провели |
перпендикуляр l к плоскости S: в |
S построили горизонталь h (h1,h2) |
|||
и фронталь f (f1,f2) и провели l1 |
M1 |
l1 |
h1 ; |
l2 M2 l2 f2. |
2. K=l

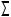 - нашли точку K пересечения перпендикуляра l и плоскости
- нашли точку K пересечения перпендикуляра l и плоскости  , для чего заключили l в плоскость Ã
, для чего заключили l в плоскость Ã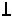 Ï2, построили прямую t=Ã
Ï2, построили прямую t=Ã

 ,
,
а затем точку K=t l. |
3. |
M, |
= M,K - из прямоугольного |
M1 K1D |
||||
нашли длину отрезка |
M,K = M1,D , равную искомому расстоянию. |
|||||||
A2 |
|
12 |
h2 |
32 |
M2 |
|
|
|
|
2 |
|
K2 |
B |
M2 |
K2 |
h2 |
|
a2 |
|
f |
|
|
|
|
|
|
2 |
2 |
t2 |
Ã2 |
l2 |
|
|
||
a1 |
|
|
42 |
|
|
|||
|
|
|
|
|
|
|
||
|
|
t1 |
|
|
|
|
|
|
|
2 |
1 |
f |
|
M1 |
|
1 |
|
A1 |
|
41 |
1 |
M1 |
|
|
||
|
|
|
M,K |
|
|
|||
h1 |
|
|
|
K1 |
h1 |
|||
|
|
|
|
|
||||
|
11 |
K |
|
M,K |
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
l1 |
|
D |
|
Рис. 5.5 |
|
Рис. 5.4 |
|
31 |
|
|
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|||

43
ПРИМЕР 5.2. Заданы точка M(M1 ,M2) и плоскость S(S1 )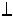 Ï1 (рис. 5.5).
Ï1 (рис. 5.5). 
 M,
M,
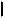 - найти расстояние от точки M до плоскости S.
- найти расстояние от точки M до плоскости S.
Пояснения к решению: 1. h |
M |
h |
- так как |
|
Ï1 , |
то |
|||
перпендикуляр к является горизонталью h (h1 |
1). |
2. |
K=h |
|
|||||
- поскольку |
Ï1 , |
то K1 =h1 |
1, а |
K2 |
l2 . 3. |
M, |
= M,K |
- |
|
[M,K] h h Ï1 |
M,K = M1,K1 . |
|
проецирующая, |
то |
отрезок |
||||
Таким |
образом, |
если плоскость |
|||||||
перпендикуляра, определяющий расстояние от точки до плоскости, строится сразу, так как он параллелен одной из ПП. Поэтому при нахождении расстояния от точки до плоскости общего положения часто применяют преобразование чертежа, решая 3ОЗПЧ и переводя плоскость в проецирующее положение (см. пример 5.3).
ПРИМЕР 5.3. Заданы точка M(M1,M2) и плоскость S(a b) (рис. 5.6). Используя способ введения новой ПП, найти
b) (рис. 5.6). Используя способ введения новой ПП, найти  M,S
M,S - расстояние от точки M до плоскости S.
- расстояние от точки M до плоскости S.
Прямая t на рис. 5.6 отношения к примеру 5.3 не имеет.
В основе решения примера - 3ОЗПЧ и пример 5.2 (рис. 5.5). Пояснения к решению: 1. Ï3
Ï3
 Ï3
Ï3 Ï1 - задали новую ПП и сде-
Ï1 - задали новую ПП и сде-
лали плоскость |
проецирующей, получив её проекцию |
3 и проекцию |
|||||||
|
l2 |
M2 |
|
точки M3 . Для этого в плоскости |
|||||
|
|
12 |
построили |
произвольную |
горизон- |
||||
t2 |
|
|
таль h, нанесли старую x1 2 |
(M1,M2) |
|||||
|
|
|
|||||||
|
|
|
b2 |
и новую x1 |
3 h1 |
оси |
проекций и |
||
|
|
K2 |
|
через проекции 13 |
и 33 |
точек 1 и 3 |
|||
|
22 |
h2 |
плоскости провели её проекцию S3 . |
||||||
|
|
||||||||
a2 |
|
|
32 |
|
|
M3 |
l3 |
|
|
|
|
|
|
|
|
|
|
||
x1 2 |
|
l1 |
|
|
|
|
|
|
|
|
t1 |
|
|
|
M,K |
|
|
|
|
|
|
|
h3 |
33 |
|
|
|
||
|
|
M1 |
31 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
a1 |
|
|
|
K3 |
3 |
|
|
|
|
h1 |
21 |
|
|
|
|
13 |
|
|
|
|
K1 |
b1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
11 |
|
x1 |
3 |
Рис. 5.6 |
|
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
44 |
|
|
|
|
|
2. |
l |
M |
l |
- построили проекции l1 и |
l 3 |
перпендикуляра l к |
||||
плоскости S, проходящего через точку M: а) l |
S |
|
h S |
l |
h, по- |
|||||
этому l1 |
h1; б) |
Ï3 l |
l Ï3 , поэтому l3 |
3 . |
3. |
K=l |
||||
- нашли проекции точки пересечения l и S: K |
l |
K |
S, но |
Ï3 |
||||||
K3=l3 |
3 |
K1 |
l1 . Для получения K2 из K1 |
построили линию связи |
||||||
(K1 ,K2) |
x1 2 и |
отложили от x1 2 по линии связи расстояние, рав- |
||||||||
ное расстоянию от точки K3 |
до оси x1 3. Через K2 и M2 проходит l2. |
|||||||||
4. |
M, |
= |
M,K - |
искомое |
расстояние равно длине отрезка |
M,K : |
||||
[M,K] l
l 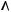 l
l 
 Ï3
Ï3 
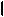 M,K
M,K =
=  M3,K3
M3,K3 .
.
ПРИМЕР 5.4. |
Заданы параллельные прямая t и плоскость |
||||||||||||
(a b) (рис. 5.6). |
|
t, - найти расстояние от прямой до плоскости. |
|||||||||||
Для выполнения примера 5.4 достаточно на |
|
|
a2 b2 |
||||||||||
прямой t взять произвольную точку M и найти рас- |
|
d2 |
|
||||||||||
стояние от неё до плоскости S с использованием |
|
|
g2 |
||||||||||
новой ПП, как в примере 5.3, или без преобразо- |
|
M2 |
|||||||||||
|
|
||||||||||||
вания КЧ, как в примере 5.1. |
|
|
|
|
|
g1 |
|||||||
|
|
|
|
|
|
||||||||
Для определения расстояния между плос- |
d1 |
||||||||||||
b1 |
|||||||||||||
костями S(a b) |
|
G(d |
g) (рис. |
5.7) достаточно |
|
|
|||||||
найти |
расстояние |
от |
какой-то |
точки |
M |
G, |
|
M1 |
a1 |
||||
например M = d |
g, |
до плоскости S так, |
как это |
|
Рис. 5.7 |
||||||||
сделано в примерах 5.1 или 5.3. |
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||
ПРИМЕР 5.5. Задана плоскость (a b) (рис. 5.8). Построить плос- |
|||||||||||||
кость |
Ã, параллельную плоскости |
и удаленную от неё на 20 мм. |
|||||||||||
Для выполнения примера надо через какую-то точку плоскости |
|||||||||||||
провести к |
отрезок перпендикуляра длиной 20 мм, а затем за- |
||||||||||||
дать плоскость Ã |
|
, проходящую через конец отрезка. |
|
||||||||||
|
e2 |
K2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
h |
2 |
2 |
|
|
|
l3 |
|
|
|
t2 |
|
|
|
|
2 |
|
|
|
|
|
||
|
M2 |
|
|
|
|
|
|
|
K3 |
Ã3 |
|||
|
a |
|
b2 |
|
|
|
|
|
|||||
|
2 |
l2 |
|
|
|
3 |
|
|
|
|
|||
x1 2 |
l1 |
|
|
|
|
|
M3 |
|
|
||||
|
|
|
|
|
|
|
13 23 |
h3 |
|||||
t1 |
|
|
|
|
|
|
|
|
|
||||
K1 |
|
|
b1 |
|
|
|
|
|
|
||||
e1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
h1 |
|
21 |
|
|
|
|
|
|||
|
|
M1 |
|
|
|
x1 |
|
|
|
|
|||
|
|
|
11 |
|
a1 |
|
3 |
|
Рис. 5.8 |
||||
|
|
|
|
|
|
|
|
|
|
||||

|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
Пояснения |
к |
решению: |
1. |
M |
|
a - в S взяли произволь- |
|||||||||
ную |
точку |
M. |
2. |
Плоскость |
S |
сделали проецирующей, |
задав |
||||||||||
Ï3 |
|
h (h - произвольная горизонталь плоскости) |
и построив её |
||||||||||||||
проекцию S3, используя |
точки |
1,M |
S. |
3. Через точку M провели |
|||||||||||||
l |
S, при этом l1 |
h1 |
(l |
S h |
S |
l |
h), а l3 |
S3 (l |
S |
S |
Ï3 |
||||||
|
l |
Ï3. 4. Так как l |
Ï3, то от M3 |
по l3 |
отложили отрезок |
длиной |
|||||||||||
20 |
мм и получили точку K3 . Точка |
K1 |
=(K3 ,K 1 ) |
l1 . Точку K2 |
|||||||||||||
нашли на линии связи, проведенной из |
|
K1 перпендикулярно оси |
|||||||||||||||
x1 |
2 , с использованием расстояния |
от |
точки |
K3 |
до |
оси |
x1 3 . |
||||||||||
5. |
à |
K Ã |
- в поле Ï3 провели Ã3 |
3, а в полях Ï1 и Ï2 плоскость |
|||||||||||||
à задали пересекающимися прямыми t |
и e ( t a |
e |
h). |
|
|
||||||||||||
|
|
5.3. Определение расстояния от точки до прямой линии |
|
||||||||||||||
|
|
Расстояние от точки до прямой линии равно длине отрезка |
|||||||||||||||
перпендикуляра, опущенного из этой точки на прямую. |
|
|
|
||||||||||||||
|
|
Расстояние |
между |
параллельными |
прямыми |
равно |
длине |
||||||||||
отрезка перпендикуляра, опущенного из произвольной точки одной прямой на другую прямую. Поэтому для определения расстояния между параллельными прямыми достаточно на одной из них взять какую-то точку и решить ключевую задачу - найти расстояние от этой точки до второй прямой.
5.9). |
ПРИМЕР 5.6. Заданы точка M(M1,M2) и прямая a(a1,a2) Ï1 (рис. |
|||||||||||
M,a - найти расстояние от точки до прямой. |
|
|
|
|
|
|||||||
a2 |
|
l2 K |
|
|
l2 |
K |
h |
2 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
||||
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
h2 |
M2 |
|
M2 |
x1 |
2 |
|
M2 |
|
|
|
|
K2 |
|
|
|
|
|
|
|
|
||||
|
h1 |
M,K |
M1 |
|
|
|
M1 |
|
|
|
|
|
|
M,K |
h1 |
|
|
M3 |
|
|
|||||
|
|
|
l1 |
|
|
|
|
|
||||
|
|
M1 |
D |
|
|
|
|
|
|
|
||
|
|
h1 |
|
l1 |
|
|
|
|
M,K |
|||
K1 |
a1 |
|
K |
|
K |
|
|
|
||||
|
1 |
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
x1 3 |
K |
3 |
h |
||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
Рис. 5.9 |
|
Рис. 5.10 |
|
|
Рис. 5.11 |
|
|
|||||
|
Пояснения к решению: 1. |
h M |
h |
a: так как |
a |
|
Ï1, то пер- |
|||||
пендикуляр к a |
параллелен |
Ï1 . 2. |
K=h a: |
K1 |
a1 |
|
K2=h2 |
|
a2. |
|||
3. M,a = M,K = M1 ,K1 : поскольку [M,K] |
h |
h |
Ï1, то отрезок [M,K] |
|||||||||
проецируется на |
Ï1 в натуральную величину. |
|
|
|
|
|
|
|||||

46
Таким образом, если прямая является проецирующей, то перпендикуляр к ней параллелен одной из ПП и расстояние от точки до прямой ищется с использованием простейших свойств прямых
частного положения. |
|
ПРИМЕР 5.7. Заданы точка M(M1 ,M2) и прямая |
h(h1 ,h2) Ï1 . |
M,h - найти расстояние от точки M до прямой h |
без преобра- |
зования КЧ (рис. 5.10) и с преобразованием КЧ (рис. 5.11). Пояснения к решению на рис. 5.10: 1.Через точку M провели пря-
мую l, пересекающую прямую h под прямым углом: построили l1 |
M1 |
||
l1 h1, нашли K1=l1 |
h1 K2 h2 и провели l2 M2,K2. 2. M,h = |
M,K - |
|
длина отрезка |
M,K |
прямой l найдена по правилу прямоугольного |
|
треугольника ( |
M1K1D), построенного в поле Ï1. |
|
|
Пояснения к решению на рис. 5.11: 1. См. пункт 1 пояснений к рис. 5.10. 2. Чтобы отрезок [M,K] прямой общего положения проецировался на ПП в натуральную величину, надо чтобы эта ПП была параллельна отрезку и, следовательно, перпендикулярна к h:
Ï3 |
h Ï3 |
Ï1 - нанесли x1 |
2 (M1,M2) и x1 3 |
h1 , построили M3 |
||
и K3 |
h3 и получили M3,K3 |
= M,K . |
|
|
||
ПРИМЕР 5.8. Заданы прямая a |
и точка |
M (рис. |
5.12). Без |
|||
преобразования КЧ найти расстояние от точки M до прямой a. |
||||||
Прямая b на рис. 5.12 отношения к примеру 5.8 не имеет. |
||||||
|
1 |
f2 |
Пример выполнялся |
согласно |
||
|
такому |
ПА (первые два пункта ПА |
||||
|
2 |
|||||
M,K |
K2 |
нужны |
для получения |
отрезка, |
||
E |
|
|||||
|
определяющего искомое расстояние): |
|||||
h2 |
M2 |
|
22 |
|
|
b2 |
|||
|
|
|
|
|
|
|
a2 |
Ã2 |
t2 |
x1 |
2 |
|
|
|
h |
|
11 |
F |
f1 |
b |
|
M1 |
K |
t |
|
|
1 |
1 |
|
|
|
a1 |
|
21 |
|
|
|
|
|
|
|
Рис. 5.12 |
|
|
1. |
M |
|
a |
(1ОМЗ) - |
горизонталью h |
M |
h |
a (h 1 a1) и |
|
фронталью f |
M |
f |
a (f2 a2) задали |
|
плоскость S |
a, содержащую множест- |
|||
во всех прямых, проходящих через точку M перпендикулярно к прямой a.
2.  K=
K=

 a (1ГПЗ) - для нахождения точки K использовались построе-
a (1ГПЗ) - для нахождения точки K использовались построе-
ния: 1. Ã
Ã a
a Ã
Ã Ï2; 2.
Ï2; 2. t=Ã
t=Ã
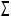 ; 3.
; 3.  K=t
K=t
 a.
a.
Через точку K пересечения прямой a с плоскостью S проходит определяющий искомое расстояние отрезок [M,K]

|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикуляра, опущенного из точки M на прямую a. |
|
|
|
|
|
|
|
|
|||||||||||
|
3. M,a = M,K (2ОМЗ): искомое расстояние - длину отрезка M,K = |
||||||||||||||||||
= E,K2 нашли из |
K2M2E, |
в котором E,M2 = K1,F . |
|
|
|
|
|
|
|
|
|||||||||
|
ПРИМЕР 5.9. |
Заданы точка M(M1 ,M2) и прямая a(a1 ,a2) |
(рис. |
||||||||||||||||
5.13). Используя способ введения новой ПП, найти |
M,a - расстояние |
||||||||||||||||||
от точки M до прямой a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Прямая b на рис. 5.13 отношения к примеру 5.9 не имеет. |
|
|
|
|
|
|
||||||||||||
|
|
22 |
a2 |
|
Цель введения новой ПП в |
||||||||||||||
|
K |
примере |
- |
сделать прямую |
|
a |
|||||||||||||
|
2 |
|
|
общего положения |
проецирую- |
||||||||||||||
|
12 |
|
b2 |
||||||||||||||||
|
M2 |
щей, чтобы несущий искомое |
|||||||||||||||||
|
|
||||||||||||||||||
x1 |
|
|
|
расстояние отрезок |
[M,K] перпен- |
||||||||||||||
2 |
|
|
дикуляра, |
опущенного из точки |
|
M |
|||||||||||||
|
11 |
M1 |
на прямую |
a, проецировался на |
|||||||||||||||
x1 |
3 |
|
|
ПП в натуральную величину. Для |
|||||||||||||||
|
K1 |
|
b1 |
этого на прямой |
a |
взяли произ- |
|||||||||||||
1 |
|
вольные точки 1, 2 и последова- |
|||||||||||||||||
3 |
21 |
|
|||||||||||||||||
|
a3 |
|
тельно задали две новые ПП: |
|
|
|
|||||||||||||
|
|
a1 |
1. Ï3 a |
|
Ï3 |
Ï1 - решали 1ОЗПЧ, |
|||||||||||||
|
M3 |
|
задавая x |
|
3 |
a |
1 |
и строя a |
3 |
1 |
3 |
,2 ; |
|
||||||
|
K3 |
x3 4 |
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|||||
|
|
2. Ï4 a |
|
Ï4 |
Ï3- решали 2ОЗПЧ, |
||||||||||||||
|
23 |
|
|
задавая x3 4 |
|
a3 и строя a4 |
|
|
14. |
||||||||||
|
|
|
|
|
Так |
как |
a |
Ï4 |
[M,K] |
|
a, то |
||||||||
|
K4 a4 14 |
|
M |
[M,K] |
Ï |
4 |
и M,K = M,a = M ,K |
4 |
. |
||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
||
|
|
M,K |
|
Точка |
K3 |
|
искалась |
из условия |
|||||||||||
|
Рис. 5.13 |
|
[M3,K3] |
|
a 3 |
(теорема о проеци- |
|||||||||||||
|
|
ровании прямого угла). |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
ПРИМЕР 5.10. Заданы прямые a |
b (рис. 5.12 и 5.13). Найти |
|||||||||||||||||
расстояние между этими прямыми. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Для нахождения расстояния между параллельными прямыми |
||||||||||||||||||
a и b на прямой b берут произвольную точку M и ищут расстояние от неё до прямой a без преобразования КЧ (см. пример 5.8 и рис. 5.12) или с использованием новой ПП (см. пример 5.9 и рис. 5.13).
5.4. Расстояние между скрещивающимися прямыми Расстояние между скрещивающимися прямыми определяется
длиной отрезка общего перпендикуляра, проведенного к обеим прямым. В учебном курсе это расстояние определяется с использованием способа введения новой ПП.

48 |
|
ПРИМЕР 5.11. Заданы скрещивающиеся прямые a Ï2 |
и b |
(рис. 5.14). a,b - найти расстояние между прямыми a и b. |
|
Пусть l - перпендикуляр к прямым a и b, пересекающий |
a в |
точке M и b в точке K ([M,K] l). Тогда искомое расстояние равно длине отрезка
l). Тогда искомое расстояние равно длине отрезка  M,K
M,K . Так как a
. Так как a Ï2, то M2
Ï2, то M2 a2. Поскольку a
a2. Поскольку a Ï2
Ï2 l
l a, то l
a, то l
 Ï2 - перпендикуляр l к прямым a и b является фронталью. Про-
Ï2 - перпендикуляр l к прямым a и b является фронталью. Про-
|
|
a M |
|
ведем через M 2 |
проекцию l2 b2 (теоре- |
|||||
b2 |
M,K |
2 |
2 |
ма о проецировании прямого угла), найдем |
||||||
|
K2 |
|
|
K2 =l2 |
b2 и с помощью линии связи K1 b1. |
|||||
l2 |
|
|
Через точку K перпендикулярно к a |
1 |
прой- |
|||||
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
дет проекция l1 |
перпендикуляра l. Точка |
|||||
|
|
l1 |
|
M1 =l1 |
a 1 . Отрезок [M,K] Ï2 , поэтому его |
|||||
|
|
|
длина |
M,K = M ,K |
2 |
. |
|
|
||
b1 |
K1 |
M1 |
|
|
2 |
|
|
|
|
|
|
a1 |
|
Таким образом для нахождения рас- |
|||||||
|
|
|
||||||||
|
Рис. 5.14 |
|
стояния между скрещивающимися прямыми |
|||||||
одну из них целесообразно сделать проецирующей, чтобы отрезок перпендикуляра, определяющий искомое расстояние, был параллелен плоскости проекций.
ПРИМЕР 5.12. Заданы скрещивающиеся прямые a и b (рис. 5.15). 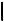
 a,b
a,b - найти расстояние между этими прямыми.
- найти расстояние между этими прямыми.
Согласно приведенной выше рекомендации прямую a сделали проецирующей, последовательно задав две новые ПП:
1. Ï3
Ï3 
 a
a  Ï3
Ï3  Ï1 (новая ось проек-
Ï1 (новая ось проек-
ций x1 3
3 a 1 ). 2.
a 1 ). 2. Ï4
Ï4 a
a Ï4
Ï4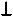 Ï3
Ï3
A2
b2
x1 2
2
b1
x1 3
3  A1
A1
(новая ось проекций |
|
x3 4 |
x3 4 a3). |
|
|
C4 |
C3 |
|
|
K4 |
a3 |
M,K |
|
D4 M4 a4
a4 B4
B4 A4
A4
 A3
A3
a2
M2 D2
|
K2 |
B2 |
C2 |
|
|
C1 |
K |
D1 |
1 |
|
|
|
|
a1
 M1
M1
K3

 B1 M3
B1 M3  D3 B3
D3 B3
b4 |
b3 |
|
Рис. 5.15 |
49
Для построения новых проекций прямых на каждой из них взяли две
произвольные точки (A и B на a, |
C и D на b). |
|
Так как a Ï4, то отрезок [M,K] - отрезок общего перпендикуляра |
||
к прямым a и b (пусть M |
a, K |
b) параллелен Ï4. Поэтому из M4 |
(M4 a4) провели [M4,K4] |
b4 и нашли искомое расстояние: a,b = |
|
=  M,K
M,K  =
=  M4,K 4
M4,K 4 . Так как K
. Так как K b
b K3
K3  b3, K1
b3, K1  b1 , K2
b1 , K2 b2. Для
b2. Для
нахождения M3, а затем M1 a1 и M2
a1 и M2 a2 из K3, используя теорему о проецировании прямого угла, опустили перпендикуляр на a3 (a
a2 из K3, используя теорему о проецировании прямого угла, опустили перпендикуляр на a3 (a 
 Ï3).
Ï3).
|
ПРИМЕР 5.13. |
|
Заданы скрещивающиеся прямые a и b (рис. |
||||||||||||||||||
5.16). |
a,b - найти расстояние между прямыми a и b. |
|
|
|
|
||||||||||||||||
|
В |
примере b |
|
Ï2 , |
поэтому |
|
|
|
|
|
|
K3 |
b3 |
|
D3 |
||||||
проецирующей делали прямую b, |
|
|
x2 |
|
|
|
|
||||||||||||||
используя новую ПП Ï3 |
b (новая |
|
|
3 |
A3 |
M,K |
|
|
|||||||||||||
ось проекций |
x2 |
3 |
|
b2). Для по- |
|
|
|
|
|
|
a3 |
|
|
|
|||||||
строения проекций a |
3 |
и b |
3 |
на пря- |
A2 |
|
K2 |
|
|
|
M |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
b. |
|
|
|
|
|
|
|
|||||
мых брали точки: A,B |
|
a и D |
|
|
|
|
|
|
|
|
B3 |
||||||||||
Расстояние |
|
a,b |
равно |
длине |
|
|
D2 |
|
|
|
|
l3 |
|||||||||
|
|
|
M |
|
|
|
|
|
|||||||||||||
отрезка |
[M,K] |
прямой |
l, |
где l |
a, |
b2 |
|
2 |
|
B |
|
|
|
||||||||
|
a2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M=l |
a , l |
b, K=l |
|
b (l M,K). |
|
|
|
|
|
|
l2 |
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пояснения к решению : |
|
|
|
|
|
|
|
l1 |
|
x1 |
2 |
|||||||||
1. В полеÏ3 |
: |
b |
Ï3 |
|
|
|
K3 |
b3; |
A1 |
|
a1 |
|
|
|
|||||||
Ï3 |
|
|
|
|
|
|
|
|
|||||||||||||
b Ï3 |
l b |
l |
|
l3 |
a3 |
|
|
|
M1 |
|
B1 |
|
|
|
|||||||
(l3 |
K3); M3 = l3 |
a 3 ; l |
|
Ï3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
[M,K] |
l |
|
M,K |
= |
|
M3,K3 . |
|
|
|
|
|
|
|
|
|
|
|
||||
2. В поле Ï2: M2 a2, |
l2 |
M2 |
l2 |
b2 |
D |
1 |
|
|
K |
|
b |
|
|
|
|||||||
(l |
b b |
Ï2), |
K2=l2 |
b2. В поле Ï1: |
|
|
|
1 |
|
1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
M1 |
a1, |
K1 |
|
b1, |
l1 |
|
|
M1 ,K1. |
|
|
|
|
Рис. 5.16 |
|
|
|
|||||
5.5. Определение натурального вида треугольника
Задача на определение натурального вида треугольника - ключевая задача для группы задач, в которую, в частности, входят задачи на определение натурального вида других плоских фигур, на построение биссектрисы угла между пересекающимися прямыми, центра окружности, вписанной в треугольник или описанной вокруг него, плоских фигур по заданным условиям.
50
Вразделе 5.5 решение ключевой задачи осуществляется только
сиспользованием способа введения новой ПП.
Плоская фигура проецируется на плоскость проекций в натуральную величину, если плоскость фигуры параллельна этой ПП.
Если плоская фигура расположена в проецирующей плоскости, то для определения натурального вида фигуры достаточно решить 4ОЗПЧ, используя одну новую ПП (рис. 3.19 и пояснения к нему).
Если плоская фигура расположена в плоскости общего положения S, то для того, чтобы плоскость S стала параллельна плоскости проекций (стала плоскостью уровня), надо последовательно задать две новые ПП (сразу задать ПП параллельно плоскости S нельзя, так
как эта ПП не будет перпендикулярна ни Ï1 , ни Ï2 ): |
|
|
|
|||||||
1. Задают |
Ï3 |
перпендикулярно горизонтали h (новая |
ось |
|||||||
x1 3 h1 ) или фронтали f |
(новая ось x2 |
3 |
f2) плоскости |
, решая |
||||||
3ОЗПЧ и делая |
проецирующей. |
|
|
|
|
|
|
|||
2. Задают Ï4 |
|
Ï4 |
Ï3 (новая ось |
x3 |
4 S3, где S3 - основная |
|||||
проекция плоскости S), решая 4ОЗПЧ. |
|
|
|
|
|
|||||
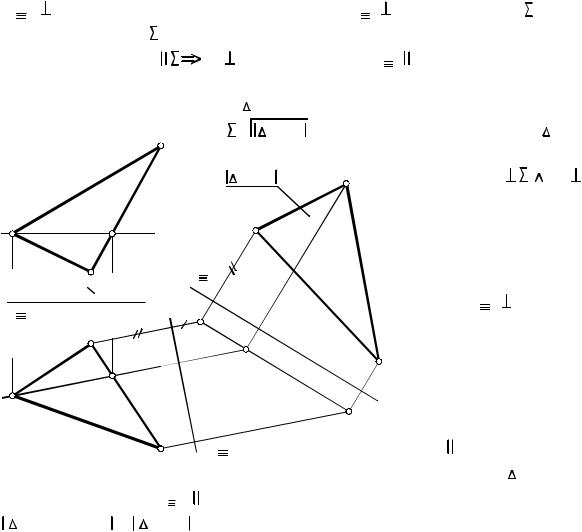
ПРИМЕР 5.14. Задан ABD (рис. 5.17), расположенный в плос- |
||||||||||
кости общего положения |
. ABD |
- найти натуральный вид |
ABD. |
|||||||
|
|
B2 |
|
|
A4 |
|
Сначала |
задали |
||
|
|
|
|
ABD |
|
новую ПП Ï3 |
|
Ï3 |
Ï1 |
|
A2 |
h2 |
|
|
D4 |
|
|
и сделали плоскость |
S |
||
|
|
|
|
проецирующей. Для этого |
||||||
|
|
x3 |
|
|
|
|
в S построили горизон- |
|||
D |
|
4 |
|
|
|
таль h(h1,h2), нанесли но- |
||||
2 |
|
|
|
|
|
|
вую ось x1 3 |
h , |
нашли |
|
x1 2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
проекции точек A3, B3, D3 |
||||
D1 |
h1 |
D3 |
|
B |
|
|||||
|
|
|
A3 |
|
и провели через них пря- |
|||||
|
|
|
|
4 |
мую S3 - основную проек- |
|||||
|
|
|
|
|
|
|
||||
A1 |
|
|
|
|
|
|
цию плоскости S. |
|
|
|
|
|
|
|
B3 |
|
Затем задали новую |
||||
|
|
|
x1 3 |
|
||||||
Рис. 5.17 |
B1 |
|
|
ПП Ï4 S и нашли нату- |
||||||
|
|
|
|
ральный вид |
ABD, про- |
|||||
|
|
|
|
|
|
|
||||
ведя новую ось x3 |
4 |
S3 и построив проекции вершин A4, B4, D4: |
||||||||
A4 B 4 D4 = |
ABD . На рис. 5.17 |
отмечены расстояния, отклады- |
||||||||
ваемые при построении проекций точки D. |
|
|
|
|
|
|||||
Натуральный вид треугольника может быть найден без преобразования чертежа определением длин его сторон по правилу прямоугольного треугольника (см. рис. 6.9 и пояснения к нему).
