
сборник задач по динамике
.pdf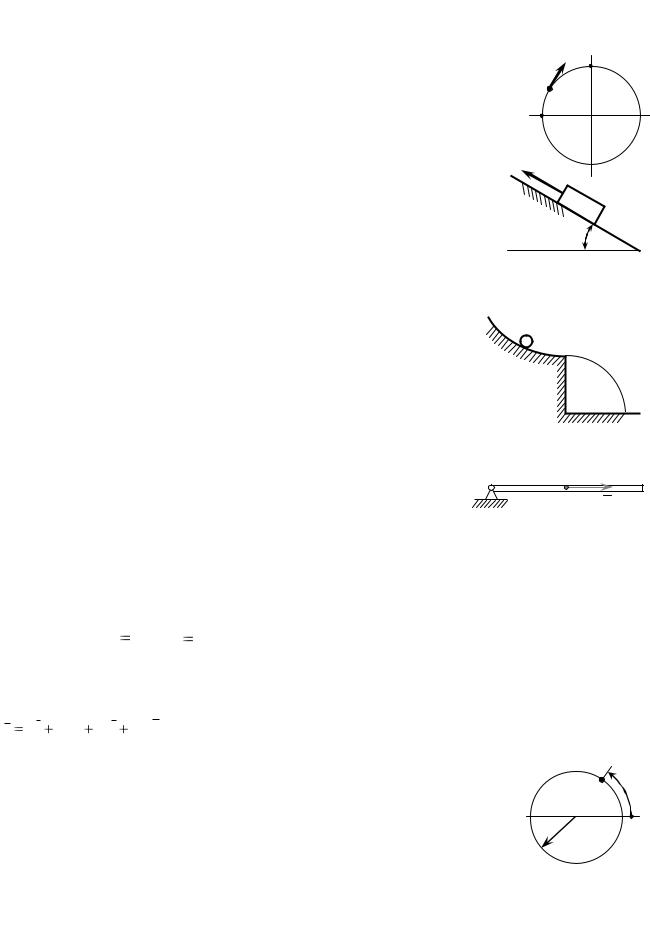
5) Тело, которому сообщили начальную скорость v0 = 6 м/с, скользило по |
|||||||||||||||
шероховатой горизонтальной плоскости и остановилось через 3 с. Найти |
|||||||||||||||
коэффициент трения скольжения. (0,2). |
|
|
|
|
|
|
v |
2 |
|
||||||
6) Материальная точка М массой m = 6 кг равномерно |
|
|
|||||||||||||
|
|
|
|
||||||||||||
движется по окружности со скоростью v = 5 м/с. Определить |
1 |
М |
|
|
|||||||||||
модуль импульса равнодействующей всех сил, действующих на |
|
|
|
||||||||||||
эту точку за время ее движения из положения 1 в положение 2. |
|
|
|
|
|||||||||||
Ответ: 5,66 Н∙с. |
|
|
|
|
|
|
|
v0 |
|
|
|||||
7) Телу, которое скользит по гладким наклонным |
|
|
|
|
|||||||||||
направляющим, сообщили начальную скорость v0 = 9,81 м/с. |
|
|
|
|
|||||||||||
Определить, через какое время тело достигнет максимальной |
|
30° |
|
||||||||||||
высоты подъема. (2 с). |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
8) Какой должен быть коэффициент трения f колес заторможенного |
|||||||||||||||
автомобиля о дорогу, если при скорости езды v = 30 м/с он останавливается |
|||||||||||||||
через 10 с после начала торможения. Ответ: 0,34. |
|
А |
|
|
|
|
|||||||||
9) Тело М, размерами которого можно пренебречь, |
в |
М |
|
|
|||||||||||
конце участка АВ приобрело скорость 15 м/с, |
|
В |
|
|
|||||||||||
|
|
|
|
||||||||||||
направленную горизонтально. Участок свободного |
|
|
|
|
|||||||||||
движения ВС оно прошло за 2,04 с. Определить величину |
|
|
|
С |
|||||||||||
скорости тела в конце участка ВС. Ответ: 25 м/с. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
10) Камень брошен вертикально вверх с начальной скоростью 30 м/с. Через |
|||||||||||||||
сколько секунд его скорость будет равна нулю? Сопротивлением воздуха |
|||||||||||||||
пренебречь. (3,58 м/с). |
|
|
|
|
|
|
О |
|
|
|
|
||||
11) Трубка равномерно вращается с угловой |
|
|
|
|
М |
vr |
|
||||||||
скоростью ω = 10 рад/с. По трубке движется шарик массой m = 2 кг. |
|||||||||||||||
Определить момент количества движения шарика относительно оси вращения |
|||||||||||||||
трубки, когда расстояние ОМ = 1,5 м и скорость шарика относительно трубки vr |
|||||||||||||||
= 2 м/с. (45 Н∙м). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
12) Материальная точка массой m = 0.5 кг движется в плоскости согласно |
|||||||||||||||
уравнениям |
x |
2t , |
y |
4t2 (м). Определить момент равнодействующей всех |
|||||||||||
приложенных к этой точке сил относительно начала координат в момент |
|||||||||||||||
времени t = 2 c (16). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
13) |
Материальная |
точка |
массой |
m |
= |
0.5 |
кг |
движется |
по |
закону |
|||||
r 2i (4t 2 |
5) j |
2t 2k |
(м). Определить производную |
по |
времени |
от |
момента |
||||||||
количества движения точки относительно начала координат. (13,4 Н∙м). |
|
||||||||||||||
14) Движение материальной точки М массой m = 10 кг |
|
|
|
s |
|||||||||||
происходит по окружности радиуса r =5 м согласно уравнению |
|
|
М |
||||||||||||
|
|
|
|||||||||||||
s = 0.5 t2. Определить момент количества движения этой точи |
|
r |
|
0 |
|||||||||||
относительно центра окружности в момент времени t |
= 2 с. |
|
|
||||||||||||
|
|
|
|
||||||||||||
Ответ: 100 Н∙м. |
|
|
|
|
|
|
|
|
|
|
|
||||
15) Материальная точка массой m = 1 кг движется по кривой. Даны |
|||||||||||||||
координаты точки: x = y = z = 1 м и проекции скорости vx = 1 м/с, vy = 2 м/с, vz = |
|||||||||||||||
4 м/с. Определить момент количества движения этой точки относительно |
|||||||||||||||
начала координат. Ответ: 3,74 Н∙м. |
|
|
|
|
|
|
|
|
|
||||||
11

3. Теорема об изменении кинетической энергии точки
Кинетической энергией материальной точки называется скалярная величина mv2 / 2 , равная половине произведения массы точки на квадрат ее
скорости. Движение точки массой m под действием силы |
|
|
|
|
определяется |
||||||||
F |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
уравнением mdv dt F , которое также можно записать в виде |
|
||||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
d (mv2 2) |
dA |
|
(3.1) |
||
mdv Fdt |
mvdv F vdt |
. |
|||||||||||
Получили теорему об изменении кинетической энергии точки в дифференциальной форме: дифференциал кинетической энергии точки равен
элементарной работе силы, действующей на точку. |
|
|||||
Интегрируя обе части уравнения (3.1) от M 0 |
до M1 , получаем |
|
||||
|
mv12 2 mv02 2 A |
|
|
|
|
(3.2) |
|
или |
T1 |
T0 A |
. |
||
Теорема об изменении кинетической энергии точки в интегральной форме: изменение кинетической энергии точки на любом перемещении равно работе силы, действующей на точку, на том же перемещении.
3.1. Относительное движение материальной точки
Пусть точка М под действием некоторых сил Fk совершает сложное
движение. Основное уравнение динамики точки относительно инерциальной (неподвижной) системы отсчета Oxyz:
|
|
|
|
|
|
|
|
|
|
|
|
|||
ma |
Fk |
m(ae ar ac ) |
Fk mar |
Fk |
( mae ) ( mac ) , |
|||||||||
где ma |
|
|
u |
– переносная сила инерции; |
|
|
|
u |
– кориолисова сила |
|||||
F |
ma |
F |
||||||||||||
e |
|
e |
|
|
|
|
|
c |
|
c |
|
|||
инерции. Таким образом, основное уравнение динамики для относительного
|
|
|
|
|
|
|
u |
|
u |
. |
|
движения запишется |
ma |
F |
F |
F |
(3.3) |
||||||
|
r |
|
k |
|
e |
c |
|
|
|||
Относительное движение материальной точки можно рассматривать как абсолютное, если действующим на точку силам прибавить переносную и кориолисову силы инерции.
Пример 3.1. Вагон весом 16 т наталкивается со скоростью 1 м/с на два упорных буфера. Определить наибольшее сжатие буферов при ударе вагона, если известно, что пружина буфера сжимается на 1см под действием силы в 5 т.
Решение. В момент соприкосновения вагона и буферов на вагон начинают действовать две силы F cx , где с = 5 т/см. Применим теорему об изменении кинетической энергии в дифференциальной форме:
d mv2 |
F dx 2 5xdx 10xdx . |
2 |
x |
|
Интегрируем слева по v от v0 = 100 см/с до нуля, а справа по х от нуля до какого-то предельного сжатия λ. Масса вагона m = 16/g = 16/981.
0 |
d |
mv2 |
10 xdx |
m1002 |
10 |
2 |
16 1002 |
5 2 |
4,04 см. |
|
2 |
2 |
981 2 |
||||||
100 |
|
0 |
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
12
Пример 3.2. Телу весом Р, лежащему на горизонтальной плоскости, сообщают начальную горизонтальную скорость v0. Требуется определить, через сколько времени тело остановится и какой путь оно пройдет до остановки, если
коэффициент трения тела о плоскость равен f (рис. 3.1). |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
N |
|
|
|||||||
Решение. По теореме об изменении количества |
|
|
|
|
|
|
|||||||
|
Fтр |
|
|
|
v |
||||||||
|
|
|
|
||||||||||
движения точки: |
mvx |
mv0 x |
Fтрt , |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
где Fтр Nf |
mgf . Поскольку vх = v0 и v0х = 0, отсюда |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
P |
|
|
|||||||
находим искомое время: t |
v0 fg . Воспользуемся |
|
|
|
Рис. 3.1 |
|
|
||||||
теоремой (3.2) |
mv2 2 |
mv2 2 |
F |
s , так как v = 0, то mv2 |
2 mgfs. |
|
|
||||||
|
|
0 |
тр |
0 |
|
|
|
|
|
|
|
|
|
Отсюда путь, пройденный телом до остановки: s v2 |
|
2 fg . |
|
|
|||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Пример 3.3. Груз весом Р, подвешенный на нити длиной l, отклоняют от |
|||||||||||||
вертикали на угол |
в положение М0 и отпускают без начальной скорости. |
||||||||||||
Определить натяжение нити в момент, когда груз дойдет до наинизшего положения М1 (рис 3.2). 
Решение. Дифференциальное уравнение движения материальной точки в проекции на главную нормаль:
|
|
mv2 l |
T |
P |
T |
mv2 l |
P , |
(1) |
|
l |
n |
|||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
где v1 |
– скорость груза в положении M1 . Для определения |
|
|
|
|
|
|
|
||||||||
|
|
T |
||||||||||||||
mv2 |
воспользуемся уравнением (3.2): mv2 |
2 mv2 2 |
A , |
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
где A |
Ph |
Pl(1 |
cos |
) |
– работа силы тяжести на М0М1. |
M 0 |
|
|
|
h |
||||||
M1 |
|
|
|
|
v |
|||||||||||
|
Учитывая условие задачи v0 |
0 , из последнего находим |
|
|
|
|
|
|||||||||
mv2 |
|
|
P |
|||||||||||||
|
2Pl(1 |
cos |
) , подставляя найденное в (1), имеем |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
|
|
|
Рис. 3.2 |
|||||
|
|
|
|
|
T |
P(3 2cos ) . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3.4. Тело 1 массой m1 = 0.5 кг удерживается в состоянии относительного покоя на гладкой поверхности призмы 2. Определить ускорение призмы 2, обеспечивающее относительный покой тела 1 (рис. 3.3).
Решение. На тело 1 действуют сила тяжести G , нормальная реакция N и переносная сила инерции Feu , направленная противоположно переносному
ускорению призмы |
a |
( F u |
ma ). Введем оси х1 и |
|
|
|
|
|
y1 |
||||
|
|
|
e |
e |
e |
|
|
|
|
|
|||
|
|
|
N |
|
|
||||||||
у1, связанные с движущейся призмой. |
|
|
x1 |
||||||||||
|
|
|
|
||||||||||
Запишем дифференциальное уравнение (3.3) |
|
|
|
|
|||||||||
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительного движения тела 1 в проекциях на |
|
|
|
|
|
Feu |
|||||||
ось х1: 0 |
Gsin30 |
F u cos30 или |
|
|
2 |
||||||||
|
|
|
|
а |
|||||||||
|
|
|
e |
|
|
30° |
|
|
e |
||||
0 |
mg sin 30 |
mae cos 30 . |
G |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда находим ускорение призмы 2: |
Рис. 3.3 |
||||||||||||
a |
|
gtg30 |
5,66 м/с2. |
||||||||||
|
|
|
|
|
|
|
|
|
|||||
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
13

Пример 3.5. Вагон трогается с постоянным ускорением a . Определить траекторию движения тела М, упавшего с полки высотой h, относительно вагона (рис. 3.4).
Решение. Вводим оси, связанные с вагоном. Указываем действующие на тело М силы: G – сила тяжести и Feu – переносная сила инерции, направленная противоположно переносному ускорению вагона a . Дифференциальные
уравнения относительного движения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
mx1 |
u |
x1 |
a, |
|
|
|
|
|
|
|
|
|
|
|
y1 |
|
|||
Fe , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
my1 |
G. |
y1 |
g. |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интегрируя, получаем |
|
|
|
|
|
|
|
Fe |
|
|
|
h |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
||||||
x1 |
at C1, |
|
x1 |
at2 |
2 C1t C3 , |
|
|
x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
G |
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
|
gt C2. |
|
y |
gt |
2 |
2 C |
t C |
. |
|
|
|
|
|
|
O1 |
|
|||
y1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
Используя начальные условия |
|
|
|
|
|
|
|
|
Рис. 3.4 |
|
|||||||||
|
|
|
0, |
|
|
0 , |
|
|
|
|
|
|
|
|
|||||
при t = 0: x1 = 0, y1 = h, x1 |
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
найдем постоянные интегрирования: С1 = С3 = С2 = 0, С4 = h. Уравнения
движения примут вид: x |
at2 2, y |
h gt2 2. |
|
1 |
1 |
|
|
Траекторию движения получим, |
исключив параметр t: y1 |
h gx1 a – |
|
уравнение прямой. Тело М упадет на пол вагона на расстоянии s |
ah g от края |
||
полки (при y1 0 x1 s ).
Если вагон будет двигаться равномерно (а = 0), то s = 0. Наблюдатель увидит траекторию – вертикальную прямую, такую же, как и при неподвижном вагоне.
|
Пример 3.6. Горизонтальная трубка длиной L м равномерно вращается |
||||||||||||||
вокруг оси Оz с угловой скоростью ω рад/с. Внутри трубки находится тело М. |
|||||||||||||||
Определить скорость тела относительно трубки в момент его вылета, если в |
|||||||||||||||
начальный момент относительная скорость v x |
x |
0 . Трением пренебречь. |
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Решение. На тело (рис. 3.5) помимо силы тяжести G и реакции от нее N1 |
||||||||||||||
будут действовать кориолисова сила инерции F u , ее реакция N |
2 |
и переносная |
|||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
сила инерции |
F u . |
По теореме об изменении кинетической энергии точки в |
|||||||||||||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
относительном движении: |
mv2 |
2 |
mv2 |
2 |
A |
A(F u ) , |
|
|
|
|
|||||
|
|
|
|
|
1 |
|
0 |
|
k |
e |
|
|
|
|
|
z |
|
|
|
|
где v0 и v1 – |
значения относительных скоростей, |
|||||||||
|
|
N1 |
|
аc |
А – работа на относительном перемещении. |
|
|||||||||
|
|
|
В нашем случае |
Ak |
0 , |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
N2 |
|
|
|
|
|
|||||||
|
аe |
М |
|
A(Feu ) |
L |
|
L |
|
m |
2 |
x02 ) . |
||||
А |
|
|
|
|
х |
maedx |
m 2 |
xdx |
|
|
(L2 |
||||
|
|
|
F u |
В |
|
|
x0 |
|
x0 |
|
|
2 |
|
||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
O |
Fcu |
G |
|
|
|
|
|
|
|
mv12 2 A(Feu ) . |
|
|
|||
Рис. 3.5 |
Откуда скорость тела в момент вылета vB |
|
|
2 |
2 |
||||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
L |
x0 . |
||||||||
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
3.2.Задачи для самостоятельного решения
1)Материальная точка массой 2.5 кг движется по горизонтальной прямой вправо со скоростью 0.4 м/с. К ней приложили постоянную силу 2 Н, направленную влево. Определить длину пути s, пройденного точкой от начала действия силы до положения, в котором точка достигает скорости 0.2 м/с, направленной влево. Определить также расстояние х между начальным и конечным положениями точки. (s = 12,5 см, x = 7,5 см).
2)Телу, положенному на шероховатую горизонтальную плоскость,
сообщили скорость v0 . Определить путь, пройденный телом до остановки, если
коэффициент трения между телом и плоскостью f. Ответ: s |
v2 |
(2 fg) . |
|
0 |
|
3) Шарик, имеющий начальную скорость v0 14 м/с, |
падает с высоты |
|
h1 1,8 м по вертикали на горизонтальный пол и отскакивает от него вверх. Определить скорость шарика на высоте h2 6,8 м от пола, не учитывая сопротивление воздуха и других потерь механической энергии.
Ответ: v 7
 2 м/с.
2 м/с.
4) Ружье весом 35 Н подвесили горизонтально на двух нерастяжимых вертикальных нитях длиной 2,55 м каждая. После выстрела каждая нить отклонилась от вертикали на угол 24°. Определить, с какой скоростью вылетела
пуля из ружья, если вес пули 0,09 Н. |
A |
R |
|
|
|
|
|
Ответ: v 809 м/с. |
|
|
|
|
R |
|
|
|
|
|
|
|
|||
5) Шарик М, размером которого |
|
|
|
|
|
||
|
|
R |
|
C |
D |
||
можно пренебречь, движется без начальной |
|
|
45° |
||||
|
|
|
|||||
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
||
скорости по дуге АВС окружности радиуса R. |
|
|
|
|
|
||
Затем шарик движется свободно. Пренебрегая трением, определить, на каком расстоянии СD от точки С шарик коснется горизонтальной плоскости. ( R
 2 ).
2 ).
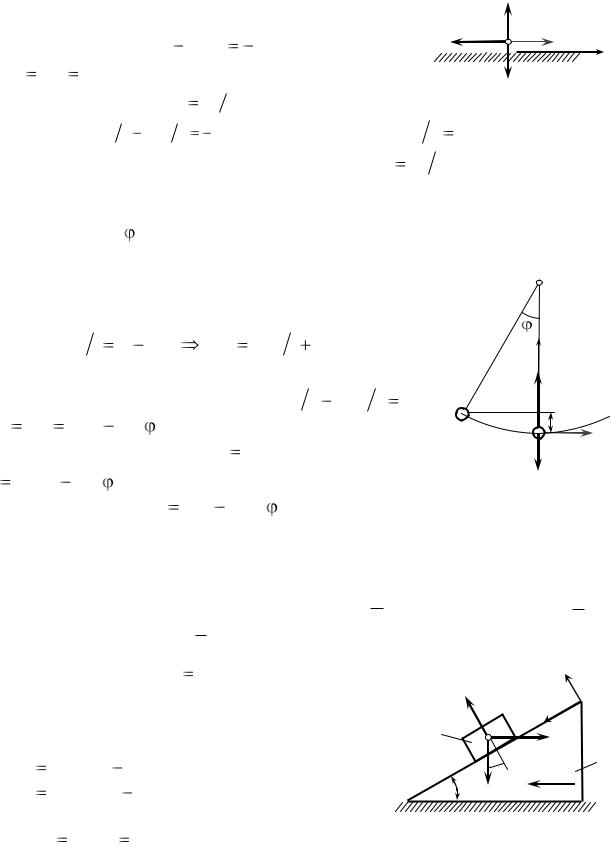
6) Вдоль наклонной грани неподвижного клина 1 |
|
|
a2 |
|
||
начал двигаться из состояния покоя клин 2. Определить |
|
|
2 |
h2 |
||
|
|
|
|
|
||
скорость клина 2 в момент, когда он, спускаясь вниз, |
h1 |
|
|
|||
коснется горизонтальной плоскости, если fтр при |
1 |
|
||||
|
|
|
|
|||
движении клина 2 равен 0,2. Известно, что a 60 см , |
|
|
|
a1 |
||
|
|
|
||||
|
1 |
|
|
|
|
|
h1 15 см , a2 20 см , h2 |
5 см . (v = 0,626 м/с). |
|
|
|
|
|
7) Маховик весом |
7,5 кН, вращаясь равномерно, |
|
делает |
900 об/мин. |
||
Определить мощность, воспринимаемую от двигателя маховиком, если диаметр вала 20 см, а коэффициент трения между валом и подшипниками 0,02. (1,414).
8) Груз М массой m может перемещаться вдоль горизонтального стержня АВ, на который надеты пружины с коэффициентами жесткости с1 и с2, которые в положении равновесия груза не напряжены. Пренебрегая весом пружин и трением, определить скорость груза М при прохождении положения
равновесия, если |
он |
был отклонен от этого положения на |
расстояние λ и |
|
отпущен без начальной скорости. |
c |
c2 |
||
1 |
M |
|||
Ответ: v2 |
|
c ) 2 m. |
|
|
(c |
|
|
||
|
1 |
2 |
|
|
15
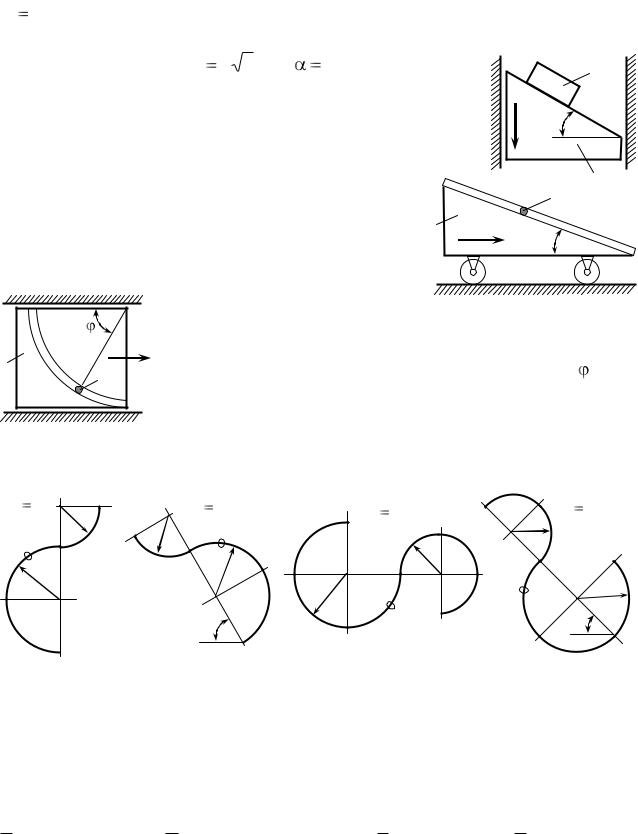
|
9) Камень брошен вверх под углом к горизонту с начальной скоростью |
||||||||||||
v0 |
21м/с. Определить: 1) скорость |
камня в момент достижения высоты h = |
|||||||||||
10 м; 2) угол, под которым он был брошен, если эта высота оказалась в два раза |
|||||||||||||
меньше максимальной. ( v |
7 5 м/с; |
|
arccos(1/ 3) ). |
|
|
|
1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10) Груз 1 массой m1 = 0.2 кг спускается вниз по |
|
|
|
|||||||||
наклонной плоскости тела 2. Тело 2 движется по вертикаль- |
|
30° |
|
||||||||||
ным |
направляющим |
вниз |
с ускорением |
а2 = |
2 |
м/с2. |
|
|
|||||
|
а2 |
|
|||||||||||
Определить силу давления груза 1 на тело 2. |
(6.76 Н). |
|
|
|
|||||||||
|
|
|
|
||||||||||
|
11) Шарик массой m1 = 0.2 кг движется из |
О |
|
|
|
2 |
|||||||
состояния относительного покоя в точке |
О по |
|
|
|
1 |
|
|||||||
гладкому цилиндрическому каналу тела 2. Тело 2 |
2 |
а2 |
|
|
|
||||||||
движется с постоянным ускорением а2 = |
2 м/с2. |
|
20° |
|
|||||||||
|
|
|
|||||||||||
Определить |
скорость |
относительного |
движения |
|
|
|
|
|
|||||
шарика в момент t = 5 c. (0.331). |
|
|
|
|
|
|
|
|
|||||
|
|
О |
|
12) Тело 1 движется по прямолинейным направляя- |
|||||||||
|
|
ющим. |
Внутри |
тела |
имеется |
канал |
в |
форме |
дуги |
||||
|
|
|
|||||||||||
|
|
а1 |
окружности, по которому перемещается шарик 2 массой |
||||||||||
1 |
|
2 |
m. Определить ускорение а1 тела 1, если при угле |
= 60° |
|||||||||
|
|
|
шарик находится в состоянии относительного покоя. |
|
|||||||||
|
|
|
|
Ответ: 5,66 м/с2. |
|
|
|
|
|
|
|||
|
13) По проволоке АВС, расположенной в вертикальной плоскости и |
||||||||||||
изогнутой в виде дуг окружностей радиусов |
R = 2 м, r =1.5 м, может скользить |
||||||||||||
без трения кольцо M массой m. Определить скорость кольца в точке С, если: |
|||||||||||||
vA 0 |
|
А |
|
vA |
0,5 м/с |
А vA 0,2 м/с |
А |
vA |
0,5 м/с |
r |
|
А |
|||||||
М |
|
|
r |
М |
|
|
r |
|
|
|
|
|
|
|
|
|
|
||
В |
|
|
|
|
r |
|
|
С |
|
|
|
|
|
|
|
В |
|||
|
|
|
|
В |
R |
В |
|
|
|
R |
|
|
|
|
|
R |
|
М |
R |
|
|
|
|
|
|
|
|||
|
|
|
|
60° |
|
М |
С |
45° |
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК
4.1. Теорема о движении центра масс Системой материальных точек (или механической системой) называют
такую совокупность материальных точек, в которой положение или движение каждой точки зависит от положения и движения всех остальных.
Все действующие на механическую систему задаваемые (активные) силы
Fk и реакции связей Nk разделяют на внешние Fke и внутренние Fki .
Внешними называют силы, действующие на точки системы со стороны материальных точек, не входящих в состав данной системы.
Внутренними называют силы, с которыми точки данной системы действуют друг на друга.
16
Центром масс системы называется геометрическая точка С, радиус-
вектор которой |
|
|
mk |
|
|
mk |
– масса системы. |
|
|||||
rC |
rk M , M |
|
|||||||||||
Координаты центра масс системы: |
|
|
|
|
|
|
|
||||||
|
xC |
mk xk M , yC |
mk yk |
|
M , zC |
mk zk M |
. |
(4.1) |
|||||
Уравнение движения системы материальных точек можно записать |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MaC |
Fke . |
|
|
(4.2) |
|||
Уравнение (4.2) выражает теорему о движении центра масс системы:
центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы,
действующие на систему. В проекциях на координатные оси, получим
MxC |
Fkxe , MyC |
Fkye , MzC |
Fkze |
. |
(4.3) |
Закон сохранения движения центра масс системы (следствия теоремы).
1. Если |
|
|
|
|
|
|
|
|
|
|
|
Fke |
0 , то из (4.2) следует, что aC 0 , откуда |
vC vC 0 |
. |
||||||||
И если vC 0 |
0, то vC 0 |
|
|
|
|
|
|
|
|
||
rC rC 0 |
. |
||||||||||
Таким образом, если геометрическая сумма всех внешних сил, действующих на систему, равна нулю, то центр масс системы движется прямолинейно и равномерно или находится в покое.
2. Если |
F e |
0, то |
x |
x |
. И если |
x |
0 , то |
x |
const или |
x |
x |
. |
|
kx |
|
C |
C 0 |
|
C 0 |
|
C |
|
C |
C 0 |
|
4.2. Теорема об изменении количества движения системы Количеством движения механической системы называют вектор K ,
равный геометрической сумме количеств движения точек системы или определяется как произведение массы всей системы на скорость ее центра масс
K  mk vk MvC .
mk vk MvC .
Запишем теорему о движении центра масс механической системы в виде
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MaC |
|
Fke F e d (MvC ) dt |
F |
e |
dK |
dt F e |
. |
(4.4) |
||||||
Уравнение (4.4) выражает теорему об изменении количества движения механической системы в дифференциальной форме: производная по времени от количества движения механической системы геометрически равна главному вектору внешних сил, действующих на эту систему.
В проекциях на оси координат имеем
|
dKx dt Fxe , dKy |
|
dt |
Fye , dKz dt Fze |
. |
(4.5) |
|||||||
Проинтегрируем уравнение (4.4) за время перехода системы из какого- |
|||||||||||||
нибудь одного положения в другое |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
e |
, |
(4.6) |
|
|
|
K |
K0 |
S |
|||||||||
где S e  Ske – полный импульс главного вектора внешних сил.
Ske – полный импульс главного вектора внешних сил.
Уравнение (4.6) выражает теорему об изменении количества движения механической системы в интегральной форме: изменение количества движения механической системы за некоторый промежуток времени равно
17
полному импульсу внешних сил, приложенных к системе, за тот же промежуток времени. В проекциях на оси координат
Kx K0x Sxe , K y K0 y Sye , Kz K0 z Sze |
. |
(4.7) |
Закон сохранения количества движения системы (следствия теоремы).
|
|
e |
|
|
e |
|
|
|
|
|
|
|
1. Если |
F |
|
F |
0 , то из (4.4) следует, что |
K const |
. |
||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, если главный вектор внешних сил, действующих на систему, равен нулю, то вектор количества движения системы будет постоянен по модулю и направлению.
2. Если |
|
|
|
|
|
|
|
|
Fxe |
Fkxe 0 , то Kx const или |
mk vkx const |
. |
(4.8) |
||||
Пример 4.1. Человек массой m1 стоит на корме лодки массой m2 |
длиной l, |
|||||||
находящейся в покое в стоящей воде. Определить, пренебрегая сопротивлением воды, расстояние , на которое переместится лодка, если человек перейдет на
нос лодки (рис 4.1). |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Система лодка-человек |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
xC 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
находится в покое под действием |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
трех внешних вертикальных сил: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
веса человека |
G1 , |
веса лодки |
G2 |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
О |
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
||||||||||||||
реакции воды |
|
N. |
Пусть x1 |
и |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x1 |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
начальные координаты |
человека |
и |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G2 |
|
|
|
|
|
|
|
|
||||||||||||||||
лодки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.1 |
|
|
|
|
|
|
|
|
||||||||||||||
Поскольку |
|
|
F e |
0 |
и начальная скорость лодки равна нулю |
x |
0 , то по |
|||||||||||||||||||||||||||||||
|
|
|
|
kx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C 0 |
|
|
|
|
|
второму закону сохранения xC |
|
const |
или xC 0 |
|
xC , где xC 0 и xC – координаты |
|||||||||||||||||||||||||||||||||
центра масс системы до перемещения и после перемещения человека по лодке соответственно. Определим их по формуле (4.1)
x |
m1x1 |
m2 x2 |
, x |
|
m1 (x1 l |
) m2 (x2 ) |
. |
C 0 |
m1 |
m2 |
C |
m1 |
m2 |
||
|
|
||||||
Приравниваем координаты центра масс до и после перемещения человека
m1x1 m2 x2 m1(x1 |
l ) m2 (x2 ) . |
Откуда находим перемещение лодки |
m1l (m1 m2 ) . |
Пример 4.2. По грани клина 1 массой М, поставленной на гладкой горизонтальной плоскости, опускается с относительной скоростью u тело 2
массой m. Определить скорость клина (рис. 4.2). |
|
|
||
Решение. Поскольку проекция главного |
|
|
||
вектора внешних сил на ось х равна нулю, согласно |
u |
|
||
второму закону сохранения количества движения |
|
mg |
||
|
|
|
|
|
системы Kx |
mk vkx const или |
|
|
|
|
mk 0vkx0 |
mk vkx . |
х |
Mg |
В начале движения количество движения |
Рис. 4.2 |
|||
|
|
|||
18
системы |
равно |
нулю |
mk 0vkx0 |
0 , т.к. |
система была неподвижна. В |
||||||||||||||
последующий момент клин начнет двигаться с некоторой скорость |
v1x |
v |
|||||||||||||||||
влево, а тело 2 будет иметь абсолютную скорость v2 x |
v |
u cos |
. Тогда |
||||||||||||||||
количество |
движения |
|
системы |
|
в |
|
последующий |
|
момент |
||||||||||
mk vkx |
Mv |
m( v |
u cos |
) |
0 , отсюда v |
mucos /(M m) . |
|
|
|
|
|||||||||
1 |
|
4.3. Задачи для самостоятельного решения |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
1) Определить ускорение тела 1, скользящего по |
||||||||||||||||
|
|
|
|||||||||||||||||
|
|
гладкой |
|
наклонной |
плоскости, |
если |
по |
горизонтали |
|||||||||||
x |
|
относительно него под действием внутренних сил системы |
|||||||||||||||||
|
|
движется тело 2 согласно закону |
x |
t2 . Массы |
тел: |
||||||||||||||
30° |
|
m1 |
m2 |
1кг. Тела движутся поступательно. (4.04). |
|
||||||||||||||
|
|
|
|||||||||||||||||
x |
|
2 |
|
2) На тело 1 действует постоянная сила F |
10 Н. |
||||||||||||||
|
1 |
Определить ускорение этого тела в момент времени |
|||||||||||||||||
F |
|
||||||||||||||||||
|
|
t 0,5 с, если относительно него движется тело 2 по |
|||||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
закону x |
cos t . Массы тел: m1 |
4 кг, |
m2 |
1кг. (2). |
||||||||||||
2 |
|
|
3) |
Тело |
1 |
массой |
m1 |
0,7 кг |
может |
двигаться по |
|||||||||
|
горизонтальной |
направляющей. |
Определить |
модуль |
|||||||||||||||
1 |
|
||||||||||||||||||
x |
ускорения тела 1 в момент времени |
t |
0,25 |
с, |
если |
||||||||||||||
|
|||||||||||||||||||
|
60° |
относительно |
него |
движется |
тело |
2 массой |
m2 |
0,1кг |
|||||||||||
|
|
согласно уравнению s |
sin 4t . (0,841). |
|
|
|
|
vA |
|||||||||||
4) Ползун |
А движется |
под действием |
силы |
F |
с |
|
|
|
|
|
|||||||||
|
|
|
|
|
А |
||||||||||||||
постоянной скоростью vA . Определить реакцию |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||
направляющей на ползун А в тот момент времени, когда |
|
|
|
|
|
F |
|||||||||||||
ускорение ползуна В равно vB |
4 м/с, |
если |
|
масса |
В |
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
однородного стержня АВ равна 5 |
кг. Массой ползунов |
|
aB |
|
|
|
|||||||||||||
пренебречь. (10). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) По платформе длины 6 м и массы 3000 кг, находившейся в начальный |
|||||||||||||||||||
момент в покое, рабочие перекатывают бочку А из левого конца платформы в |
|||||||||||||||||||
правый, а бочку В из правого конца в левый конец. Насколько переместится |
|||||||||||||||||||
при этом платформа, если общая масса бочки А и рабочих равна 500 кг, а бочки |
|||||||||||||||||||
В и рабочих равна 900 кг? (6/11). |
|
|
|
|
|
|
|
|
1 |
|
|
|
l |
||||||
6) Тело 1 массой 4 кг может двигаться по горизонталь- |
|
|
|
|
|
||||||||||||||
ной направляющей. На какое расстояние переместится тело 1, |
|
|
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
когда однородный стержень 2 массой 2 кг и длиной 0.6 м, опускаясь под |
|||||||||||||||||||
действием силы тяжести, займет вертикальное положение. В начальный момент |
|||||||||||||||||||
система находилась в покое. |
(0.1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7) Моторная лодка весом 4 кН, двигаясь по реке, приобретает постоянную |
|||||||||||||||||||
скорость 7 м/с. После натяжения каната вслед за лодкой из состояния покоя |
|||||||||||||||||||
начал двигаться |
прикрепленный к |
канату плот весом 7,2 кН. Считая, что |
|||||||||||||||||
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|

движущая сила и силы сопротивления уравновешиваются, определить |
|
|||
скорость, с которой лодка и плот продолжают двигаться вместе. (2,5 м/с). |
|
|
||
8) Рыбак весом G1 = 800 Н сидит на корме лодки, а второй весом G2 = 600 Н |
|
|||
на носовой части. Лодка весом G3 = 1000 Н и длиной 4 м, находящейся в покое |
|
|||
в стоящей воде. Определить, пренебрегая сопротивлением воды, расстояние, на |
|
|||
которое переместится лодка, если рыбаки поменяются местами. (1/3 м). |
|
|
||
9) На средней скамейке лодки, находившейся в покое, сидят два человека. |
|
|||
Один из них, массы m1 = 50 кг, переместился вправо на нос лодки. На какое |
|
|||
расстояние должен переместиться 2-й человек массы m2 = 70 кг для того, чтобы |
|
|||
лодка осталась в покое. Длина лодки 4 м. Сопротивлением воды движению |
|
|||
лодки пренебречь. (10/7 м). |
|
2 |
|
|
10) Клин 1 весом 70 Н размещен на гладкой |
|
|
|
|
|
|
1 |
|
|
горизонтальной плоскости. Пружину сжали и тело 2 |
|
|
|
|
|
|
|
|
|
весом 30 Н отпустили из состояния покоя. Определить |
|
30° |
|
|
расстояние, на которое переместится клин, если тело 2 |
|
|
|
|
прошло 40 см по наклонной грани клина. (10,4 см). |
|
2 |
|
|
11) Три груза массой m1 = 20 кг, m2 = 15 кг и m3 = 10 кг |
3 |
|
|
|
соединены нерастяжимой нитью. Пренебрегая трением |
B |
C |
|
|
|
1 |
|||
между усеченной пирамидой и полом, определить |
|
|
|
|
|
|
|
|
|
перемещение усеченной пирамиды АВСD массы M = |
A |
60° |
D |
|
100 кг относительно пола, если груз 1 опустится вниз на |
|
|
||
|
|
|
|
|
1 м. Массой нити пренебречь. (Влево на 14 см). |
|
|
|
|
12) Лодку весом 1 кН вместе с человеком, вес которого 0,6 кН, несет |
|
|||
течение реки. Человек стал переходить по дну лодки в направлении, |
|
|||
противоположном движению реки, со скоростью 0,8 м/с относительно лодки. |
|
|||
Пренебрегая сопротивлением воды, определить скорость лодки во время |
|
|||
перемещения человека, если скорость течения равна 0,5 м/с. (0,8 м/с) |
|
|
||
13) В лодке весом 900 Н, которую несет течение реки, сидят два человека |
|
|||
весом 500 Н и 700 Н. Чтобы поменяться местами, человек весом 500 Н |
|
|||
переходит по лодке в направлении течения реки со скоростью 0,6 м/с |
|
|||
относительно лодки, а второй в это же время движется в противоположном |
|
|||
направлении с относительной с относительной скоростью 0,2 м/с. Пренебрегая |
|
|||
сопротивлением воды, определить скорость лодки во время перемещения |
|
|||
людей, если скорость течения 0,4 м/с. (0,324 м/с). |
|
|
|
|
5. Теорема об изменении кинетического момента системы Моментом инерции тела (системы) относительно данной оси Оz
называется скалярная величина, равная сумме произведений масс всех точек
тела (системы) на квадраты их расстояний от этой оси: J |
z |
m h2 . |
|
|
k |
k |
|
Моменты инерции: |
|
|
|
– однородного стержня относительно центр масс стержня Jz |
Ml2 12; |
||
– тонкой цилиндрической оболочки относительно ее оси J z |
MR2 ; |
||
– круглого однородного цилиндра относительно его оси J z |
MR2 2 . |
||
20
