
- •Тема 3. Информационно-логические основы построения эвм лекция 3.1. Позиционные системы счисления
- •Основные понятия систем счисления
- •Представление целых неотрицательных чисел
- •Перевод целых чисел
- •Представление дробных чисел
- •Перевод дробных чисел
- •Арифметические действия над числами
- •Представление отрицательных двоичных чисел.
Арифметические действия над числами
Для выполнения арифметических операций над числами, представленными в любой системе счисления надо пользоваться известными правилами арифметики:
Сложение многоразрядных чисел начинается с младшего разряда, производится поразрядно с учетом единиц переноса из предыдущих разрядов.
Вычитание двух многоразрядных чисел начинается с младших разрядов с учетом при необходимости переноса единиц (количество которых соответствует основанию системы счисления) из старших разрядов.
Умножение и деление двух многоразрядных чисел в любой системе счисления выполняется по правилам десятичной системы счисления.
При двоичном умножении частичное произведение равно 0, если множитель равен 0, и равно множимому, если множитель равен 1. Таким образом, в процессорах операция двоичного умножения выполняется путем сдвига влево и сложения множимого. Аналогично операция двоичного деления выполняется путем сдвига вправо делителя и вычитания его из делимого.
С![]() уществует
еще одна арифметическая операция, часто
выполняемая над двоичными числами –
сложение по модулю 2. Эта операция
выполняется поразрядно и определяется
следующим образом:
уществует
еще одна арифметическая операция, часто
выполняемая над двоичными числами –
сложение по модулю 2. Эта операция
выполняется поразрядно и определяется
следующим образом:
Здесь полная аналогия с операцией «остаток от деления на 2» A mod 2, которая означает, что число A делится на 2 и заменяется остатком (например, 9 mod 2 = 1). Так и в случае сложения по модулю 2 сумма разрядов делится на 2 и заменяется остатком (например, 2 mod 2 = 0).
Представление отрицательных двоичных чисел.
Существует несколько способов представления отрицательных двоичных чисел.
Прямой (натуральный, симметричный, знаковеличинный) код. Согласно этому коду число представляется посредством значения и знака, причем значение записывается в двоичной системе счисления, а бит знака занимает самый старший разряд поля представления двоичного числа. Если число положительное, то бит знака равен 0, если отрицательное, то 1.
Пример 3.4. Семиразрядный натуральный двоичный код числа 2810 = 00111002. Так как число положительное, то к указанному коду следует приписать слева 0 (бит положительного знака): [00111002]пр. = 0.00111002.
Если же число отрицательное (-2810), то требуется добавить 1 (бит отрицательного знака): [-00111002]пр. =1.00111002.
Такой способ представления используется при выводе чисел на индикацию, а также в некоторых аналого-цифровых преобразователях.
При представлении чисел в прямом коде реализация арифметических операций в ЭВМ должна предусматривать различные действия с модулями чисел в зависимости от их знаков. Для упрощения выполнения арифметических операций используют специальные коды, позволяющие свести операцию вычитания к операции сложения.
Обратный код. Обратный код отрицательного двоичного числа формируется заменой всех нулей симметричного кода этого числа на единицы, а всех единиц на нули, кроме бита знака. Обратный код числа [-00111002]обр. = 1.11000112.
Принято, что обратный код положительного числа полностью соответствует прямому.
Возможно получение обратного кода отрицательного числа в любой системе счисления. В этом случае цифры числа определяются из соотношения
![]()
где m – основание системы счисления, a – цифра числа, записанного в прямом коде.
Дополнительный код. Прежде чем говорить об этом способе представления отрицательных чисел, дадим следующее определение.
Дополнение числа определяется как величина, которая, будучи прибавлена к данному числу, обращает сумму в нуль с переносом единицы в старший разряд.
Пример 3.5. 68110 и 31910 в сумме дают 1000 (т.е. нули с переносом единицы в старший разряд). Таким образом, 681 является дополнением числа 319, а 319 – дополнение к числу 681.
Пример 3.6. 1012 и 0112 в сумме дают 1000 (т.е. нули с переносом единицы в старший разряд). Таким образом, 101 является дополнением числа 011, а 011 – дополнение к числу 101.
Или более строго:
Дополнением числа A будет число Aдоп = K – A > 0, где K = mn – константа дополнения, m – основание системы счисления, n – максимальное количество разрядов для представления чисел.
Пример 3.7. Пусть m=10, n=7, A=75, тогда K=107=1000000010,
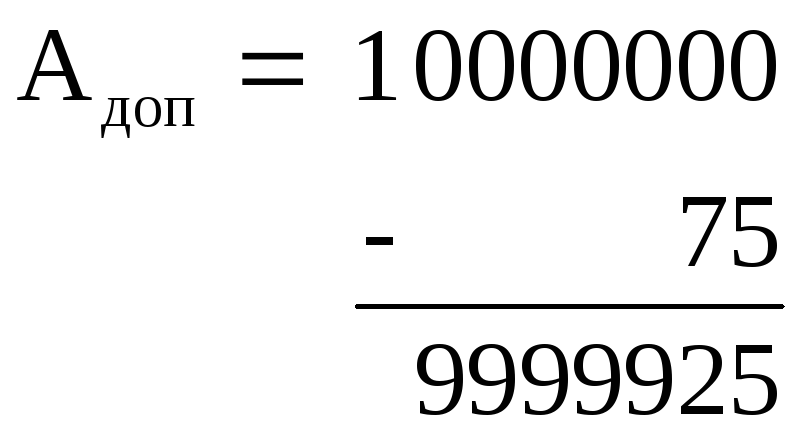
Пример 3.8. Пусть m=2, n=7, A=11, тогда K=27=100000002,
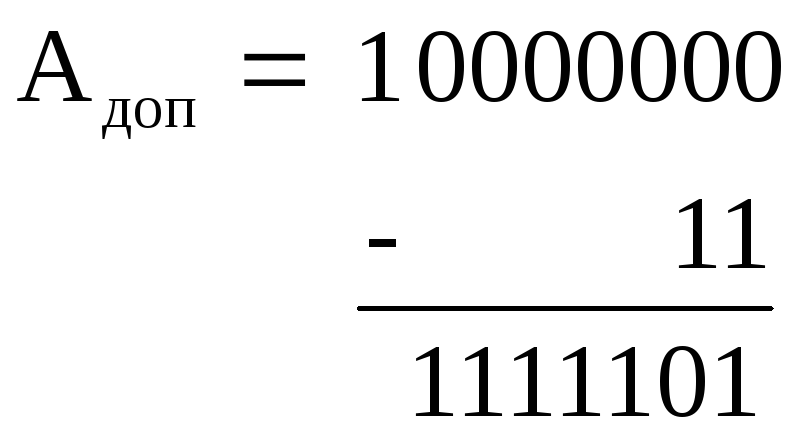
Для поиска дополнения можно пользоваться и таким приемом.
Для того чтобы получить дополнение для любого числа надо вычесть каждую цифру числа из наибольшего цифрового значения для данной системы счисления и прибавить единицу к цифре младшего разряда.
Отсюда с учетом (3.9) получаем правило: для получения дополнительного кода отрицательного числа надо к обратному коду числа прибавить единицу. Принято также, что дополнительный код положительного числа совпадает с прямым кодом.
Обратите внимание, что во всех представления старший разряд несет информацию о знаке числа.
В ЭВМ для представления отрицательных чисел и выполнения двоичных арифметических операций над целыми числами используется дополнительный код. При этом арифметические операции над двоичными числами без знака ничем не отличаются от подобных операций над двоичными числами со знаком, если они представлены своими дополнительными кодами.
Вычитание С = А - В при этом выполняется следующим образом:
определяется дополнительный код вычитаемого В и производится сложение этого кода с уменьшаемым А; перед преобразованием прямых кодов в дополнительные необходимо их выровнять по числу разрядов.
если разность – число положительное, то бит переноса из старшего (знакового) разряда необходимо отбросить (тем самым как бы удалить из результата константу дополнения).
Сущность заключается в том, что вычитаемое В, как отрицательное число, представляется в виде дополнения до константы К = mn, при которой выполняется условие К - В > 0. Следовательно, операцию С = A - B, где А и В целые положительные числа в любой системе счисления, можно представить в виде
С = А - В = А + (-В )=А + (mn - B) -mn, (3.10)
где m — основание любой системы счисления; mn – константа образования дополнительного кода, n – количество разрядов для представления чисел. Из выражения для разности (3.10) следует, что из полученной суммы нужно исключить добавленную константу.
Пример 3.9. Пусть необходимо найти разность 5 – 2:
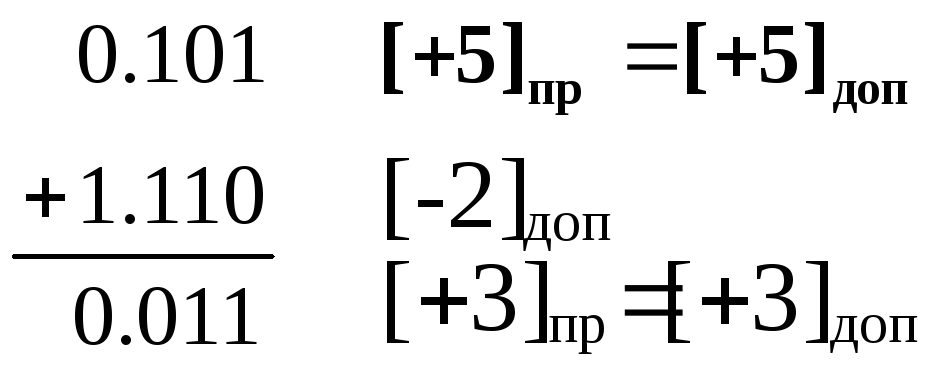
если разность – число отрицательное (бит старшего разряда 1), то результат представлен в дополнительном коде (константа дополнения осталась в результате). Для определения абсолютного значения отрицательного результата, необходимо применить к нему операцию вычисления дополнения (т.к. дополнение от дополнения есть исходное число).
Пример 3.10. Пусть необходимо найти разность 2 – 5:

Из примеров 3.9 и 3.10 следует, что при сложении чисел с разными знаками единица переноса из старшего (знакового) разряда является признаком положительного результата, отсутствие переноса – признаком отрицательного результата, при этом константа образования дополнительного кода не скомпенсирована и осталась в сумме.
При сложении чисел с одинаковыми знаками признаки противоположны: отсутствие переноса единицы из старшего разряда при положительных слагаемых является признаком положительного результата, а наличие переноса при отрицательных слагаемых – признаком отрицательного при этом одна константа компенсируется переносом, а вторая сохраняется в сумме.
Кроме того, в некоторых случаях может произойти переполнение разрядной сетки. Результат сложения чисел при переполнении является неверным.
Можно выполнять алгебраическое сложение чисел, представленных и в обратных кодах, только надо помнить, что бит переноса из знакового разряда надо добавить в младший разряд результата.
Объясним это. По сути обратный и дополнительный коды отличаются выбором значения константы К: mn – константа образования дополнительного кода, а mn - 1 — константа образования обратного кода.
Выражение (3.10) можно представить в виде
С = А - В = А + (-В )=А + (mn - 1 - B) - mn + 1 (3.11)
здесь mn -1 – константа образования обратного кода. Из выражения для разности следует, что из полученной суммы также нужно исключить добавленную константу (- mn + 1). Но для этого надо исключить 1 переноса из знакового разряда (т.е. mn ) и добавить 1 к младшему разряду суммы, т.е. требуется дополнительная операция сложения. Именно поэтому в ЭВМ для выполнения действий используется дополнительный код, а обратный только для образования дополнительного кода.
Пример 3.11. Пусть необходимо найти разность 5 – 2 используя обратный код:
![]()
