Задачи линейного программирования, не требующие для решения специальных методов

Рассматривается задача о рациональной организации снабжения центра однородной продукцией из n-пунктов. Пусть – количество продукции, поставляемое в центр изi-го пункта, а – стоимость производства и перевозки единицы продукции изi-го пункта. Стоимость всей продукции, доставленной в центр, определяется по формуле

. (1.10)

Требуется организовать рациональное снабжение центра, т.е. выбрать таким образом, чтобы обеспечить минимальную стоимость продукции в центре. При этом на задачу накладываются следующие ограничения:

• потребность центра в продукции определяется величиной , т.е.

, (1.11)

а излишков продукции быть не должно;

• производство продукции в i-м пункте ограничено величиной , а пропускная способность транспорта изi-го пункта ограничено величиной .

Пусть , где. Тогда

. (1.12)

Таким образом, получена задача линейного программирования. Нетрудно заметить, что наиболее рациональна доставка продукции из пункта, где ее стоимость наименьшая. Перенумеруем пункты в порядке возрастания стоимости

.

Из первого пункта, в котором стоимость единицы продукты наименьшая, центр может получить единиц продукции. При этом могут возникнуть две ситуации:

1. ;

2. .

В первом случае центр полностью удовлетворяет свою потребность за счет первого пункта. Решение задачи будет иметь вид

.

Во втором случае первый пункт удовлетворяет лишь часть потребности, т.е.

.

Тогда получается задача, аналогичная предыдущей, с той лишь разницей, что потребность в продукции определяется величиной , а количество поставщиков составит.

Из второго пункта центр может получить единиц продукции. При этом могут возникнуть две ситуации:

1. ;

2. .

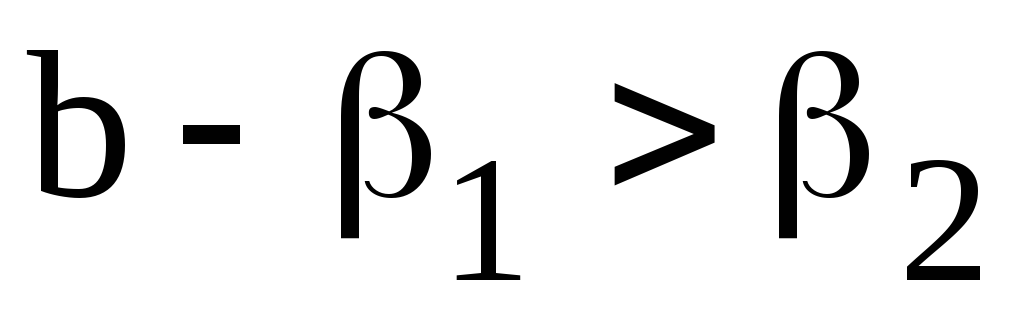В первом случае центр полностью удовлетворяет свою потребность за счет первого и второго пунктов. Решение задачи будет иметь вид

.

Во втором случае второй пункт совместно с первым удовлетворяют лишь часть потребности центра

,

т.е. получается задача, аналогичная предыдущей, с той лишь разницей, что потребность определяется теперь величиной , а количество поставщиков составит.

Продолжая решать задачу по приведенной схеме, можно столкнуться с одной из двух ситуаций:

1. ;

2. .

В первом случае невозможно полностью удовлетворить потребность центра в продукции. Во втором случае потребность будет удовлетворена полностью.

Определим индекс следующим образом

;

.

Тогда решение задачи будет иметь вид

.

Задача о рациональном снабжении центра решается таким простым способом лишь потому, что ее условие содержит только одно ограничение, связывающее все переменные .

Пример 1.2. Три машиностроительных предприятия снабжают головное предприятие комплектующими изделиями. Первое предприятие способно поставить 50 тыс.шт. по 10 тыс.руб. за 1 шт., второе − 30 тыс.шт. по 8 тыс.руб. за 1 шт., третье – 45 тыс.шт. по 9 тыс.руб. за 1 шт. Организовать рациональное снабжение головного предприятия комплектующими изделиями при условии, что пропускная способность транспорта с первого предприятия 60 тыс.шт., со второго – 25 тыс.шт., с третьего – 50 тыс.шт., а головному предприятию по плану необходимо иметь комплектующих изделий 100 тыс.шт.