Графический метод решения задачи линейного программирования

Простейшим методом решения задачи линейного программирования является графический. Графический метод используется для получения решения задач, в которых участвуют в рассмотрении только две переменные. Графический метод решения задачи линейного программирования предусматривает осуществление следующих этапов:

1. Строится многоугольная область допустимых решений.

2. Строится вектор-градиент целевой функции.

3. Линия уровня 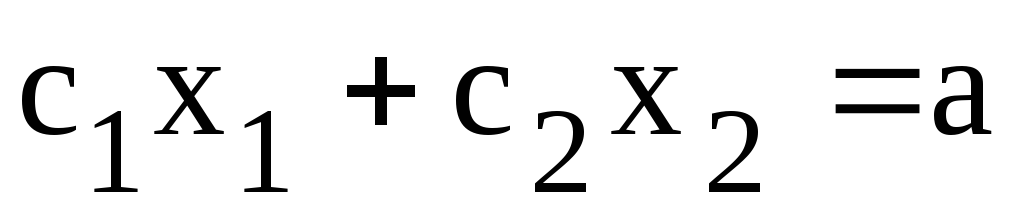(где- постоянная величина) − прямая, перпендикулярная вектору-градиенту — передвигается в направлении этого вектора в случае максимизации целевой функции до тех пор, пока не покинет пределов области допустимых решений. Предельная точка (или точки) области допустимых решений при этом движении и является точкой максимума целевой функции.

При минимизации целевой функции линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает области допустимых решений, то соответствующий максимум или минимум целевой функции не существует.

Использование графического метода для решения задач линейного программирования рассмотрим на примере 1.1.

Пример 1.1. Изготовление двух видов изделий А и Б включает выполнение трех операций. Трудоемкость обработки каждого изделия на этих операциях, фонды времени и прибыль на единицу изделия приведены в табл.. 1.1.

Таблица 1.1

Группа оборудования	Трудоемкость, нормо-час.		Фонд времени, час.
	А	Б
Токарная	1	5	28
Фрезерная	4	3	27
Шлифовальная	2	-	10
Прибыль на единицу изделия, тыс.руб.	2	4	-

Решение

Этап 1. Математическая постановка задачи.

Пусть – количество выпускаемых изделий вида А;– количество выпускаемых изделий вида Б. Тогда целевая функция примет вид

при ограничениях

Этап 2. Графическое решение задачи.

На плоскости построим декартову систему координат (рис. 1.1). На горизонтальной оси наносим значения переменной , на вертикальной –. Неравенства (1.5) - (1.9) на графике изображаются в виде полуплоскостей, ограниченных соответствующими прямыми:

1. ;

2. ;

3. ;

4. ;

5. .

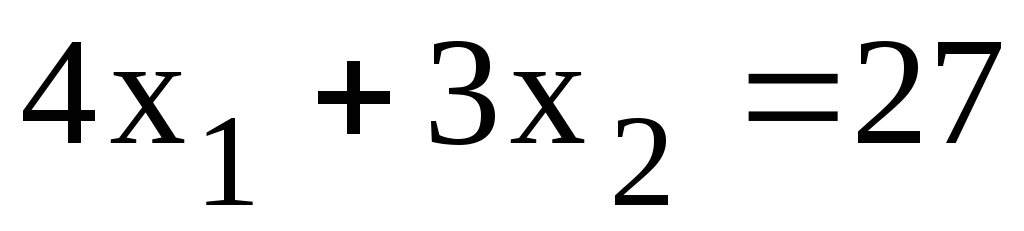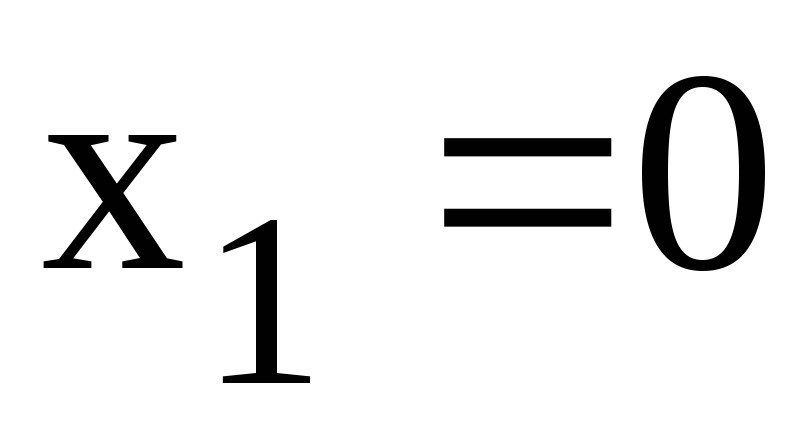Рис. 1.1. Графическое решение задачи определения оптимального плана

производства двух видов изделий

Пять полуплоскостей образуют область определения целевой функции, которая называется областью допустимых решений (область ОДР, заштрихована).

Задача заключается в том, чтобы из всех точек области ОДР найти такую, в которой целевая функция принимает максимальное значение. Известно, что если целевая функция имеет экстремум в ОДР, то он обычно достигается в вершине ОДР.

Для рассматриваемой задачи многоугольник, образующий ОДР, имеет пять вершин. Для выбора вершины, дающей максимум целевой функции, необходимо построить градиент. Градиент – это радиус-вектор, выходящий из начала координат и показывающий направление наискорейшего роста функции. Для построения градиента необходимы две точки, одной из которых будет начало координат, а другую определим по формуле:

,

где - радиус-векторы, совпадающие с координатными осямии.

Тогда

,

т. е. вторая точка будет иметь координаты (2, 4).

Построив градиент (рис. 1.1), легко можно определить единственную точку, дающую максимум целевой функции. Эта точка А с координатами (3, 5).

Таким образом, целевая функция достигает максимума при

.

Этап 3. Анализ полученного результата.

Оптимальным планом производства для машиностроительного предприятия будет выпуск изделия А в количестве 3 шт. и изделия Б – 5 шт., при этом предприятие получит максимальную прибыль в размере 26 тыс.руб.

Задача 1.1. Изготовление двух видов изделий А и Б включает выполнение четырех операций. Трудоемкость обработки каждого изделия на этих операциях, фонды времени и прибыль на единицу изделия приведены в табл. 1.2.

Таблица 1.2

Номер операции	Трудоемкость обработки изделия, нормо-ч		Фонд времени, ч
	А	Б
1	2	6	32
2	-	2	8
3	4	2	34
4	3	-	24
Прибыль на единицу изделия, усл.ед.	3	2

Определить, сколько изделий каждого вида необходимо выпустить для получения максимальной прибыли.