Т3 Логика решения задач

методы решения задач. В многослойных методах сложная задача разбивается на последовательные слои частных подзадач, имеющих более простое решение. Решение указанных частных подзадач приводит к решению сложной задачи в целом.

_______________________________________

450. После того, как тем или иным методом была формально решена задача оптимизации, следующим этапом исследований (L2. s .2) является

содержательный анализ полученного решения.

460. Прежде всего, полученное решение должно быть проанализировано в рамках исходной постановки задачи (14)–(27). Необходимо вычислить все достигнутые значения показателей и проверить выполнение всех ограничений. Тем самым будет построена содержательная интерпретация полученного решения в терминах планируемой операции.

470. На основе содержательной интерпретации полученного решения строится соответствующий план операции, который представляет собой упорядоченную последовательность средств и промежуточных целей с определенными значениями их параметров и показателей.

480. Так, если исходить из структуры целей и средств (рис. 3.3.1), то полученное решение позволит из альтернативных вариантов курсов действий по достижению генеральной цели выбрать оптимальный курс действий, который можно формально представить в виде:

{ iopt : i I 0 } { iopt : i I 1 } { iopt : i I 2 } ...

средств, промежуточных целей (средств) этапов и конечная цель соответственно; I 0 , I k - множества индексов исходных средств и

промежуточных целей (средств) на соответствующем этапе. Соответственно каждому этапу можно поставить в соответствие

расчетные значения параметров и показателей операции:

{( k ; x, z, y, p) : k 0, 1, 2, ... , T}. (34)

490. Далее, целесообразно построить подробный сценарий, реализующий полученный план операции. В результате сценарной отработки полученного плана может оказаться, что результаты операции не удовлетворяют ЛПР по ряду показателей и ограничений. Особо это относится к весовым оценкам частных показателей, базовых возмущений

204

среды и внутренних состояний, на основе которых решалась поставленная задача. В итоге формально оптимальное решение может оказаться неэффективным. В результате ЛПР может принять решение об изменении данных исходной постановки задачи с целью достижения приемлемых результатов.

____________________________________________

500. В целом выбор эффективного решения (L2. s . s ) представляет

собой интерактивную процедуру принятия решений, включающую в себя как формальные методы выбора оптимальных решений, так и содержательный анализ полученных решений с последующей коррекцией постановки задачи.

510. При выборе эффективных решений необходимо руководствоваться следующими особенностями данных задач.

Для наглядности изложения на рис. 3.3.2 представлена характерная зависимость двух нормированных показателей в задаче выбора решений.

Рис.3.3.2. Область Парето в задаче выбора решений

Здесь на рис. 3.3.2 приведена плоскость всевозможных значений показателей (g1, g2 ) . Заштрихованная область G представляет наборы

значений показателей (g1, g2 ) , которым соответствуют определенные

задачи они являются невыполнимыми.

205

Если сформулировать обобщенный показатель в виде взвешенной суммы частных показателей

то выражению (35) будет соответствовать некоторая прямая L в плоскости

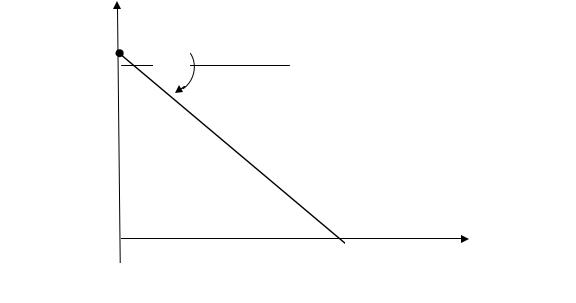
(g1, g2 ) (см. рис. 3.3.3).

g2

tg( ) 1

L

1 2

g1

1 1g0

Рис. 3.3.3. Геометрическая интерпретация обобщенного показателя

С учетом сказанного рассмотрим геометрическую интерпретацию решения задачи оптимизации на рис. 3.3.2.

Минимизация обобщенного показателя (35) означает параллельный сдвиг прямой L по направлению к началу координат, как конечной цели. Это движение имеет предел, определяемый точкой C на границе области возможных решений G . Это и есть точка оптимального решения. Изменение коэффициентов 1 , 2 передвигает точку оптимальных

решений по границе Г области возможных решений G . В крайних случаях оптимальное решение соответствует точкам А и В. В точке А оптимизация

показатель g2 - максимальное значение g2,max . Напротив, в точке В показатель g1 имеет максимальное значение g1,max , показатель g2 - минимальное значение g2,min . В промежуточной точке С значения показателей имеют промежуточные значения g1,0 , g2,0 .

Граница Г области возможных решений G называется область Парето17, или область неулучшаемых решений. Действительно, решения при планировании операций можно принимать самые разнообразные вплоть до самых неэффективных решений с бесполезной тратой ресурсов. Оптимальные же решения предполагают минимальный расход ресурсов, использование всех имеющихся резервов для достижения цели. Однако оптимальные решения зависят от вида выбранного критерия оптимизации. Решения, оптимальные по одному критерию, не оптимальны по другому критерию и противоречат друг другу. Это хорошо видно на рис. 3.3.2. Улучшение решения в области Парето по одному показателю приводит к ухудшению решения по другому показателю. Лишь для неэффективных решений можно достичь улучшения решения по всем показателям. Для эффективных решений вследствие объективных ограничений это сделать невозможно. Более того, сам выход на противоречия свидетельствует о выходе в область эффективных решений. Это общее правило при планировании операций.

520. Главной задачей при планировании операции является получение эффективного плана операции. Это можно сделать в самых разнообразных постановках задач.

Так эффективное решение в точке С области Парето на рис. 3.3.2 можно получить следующими способами:

- на основе минимизации обобщенного показателя

g0 1,0 g1 2,0 g2 ;

- на основе задач оптимизации при ограничениях:

- на основе наложения ограничений:

17 Парето (Pareto), Вилфредо (1848-1923) – итальянский экономист и политический философ. Впервые выдвинул учение об обществе как о саморегулирующейся и развивающейся по своим законам системе, независимо от воли и контроля человека. Парето выдвинул понятие оптимальности, состоящее в том, что оптимальные экономические условия в обществе – условия, при которых никто не может стать богаче без того, чтобы хотя бы один человек не стал беднее.

207

Далее, можно поставить задачу оптимизации на основе

Совершенно аналогично решается и обратная задача: найти

условный экстремум min g1 (x) , при ограничении типа равенства

(x)

g2 (x) g2,0 . Результат решения согласно (рис. 3.3.2) будет полностью

соответствовать решению предыдущей задачи.

Далее, можно поставить задачу с неравенствами: найти условный

экстремум min g2 (x) , при ограничении типа равенства

(x)

Рекуррентная процедура решения задачи здесь будет иметь вид

В соответствии с (рис. 3.3.2) решение и этой задачи будет совпадать с предыдущими. Здесь также может быть поставлена и противоположная задача. Конечное решение от этого не изменится.

Отметим также, что при условиях:

постановка задачи будет противоречивой и не иметь решения. Здесь интересно отметить, что если применить для подобных задач процедуру автоматического поиска весовых коэффициентов, то коэффициенты для несовместных условий будут бесконечно расти. Если подобные коэффициенты нормировать, то коэффициент при несовместном условии будет стремиться к единице, а все остальные коэффициенты будут стремиться к нулю. Это означает, что для жестко поставленных несовместных ограничений критерий оптимизации трансформируется в единственный критерий достижения несовместного ограничения. Другими

208

словами, происходит смена цели оптимизации, которая становится ориентированной на преодоление критического ограничения. Формально преодолеть данное противоречие невозможно, и оно разрешается на основе изменения условий постановки задачи. Область Парето при этом деформируется так, чтобы включить в область допустимых решений критическое ограничение.

530. Для эффективного решения подобных задач можно использовать схему исследований с выделением контраста противоречий. Подобный подход в принятии решений, который можно назвать методом «крайних точек», состоит в том, что на первом этапе решения выделяются частные решения, которые соответствуют экстремумам частных показателей. Далее, на основе анализа частных решений и выявления причин, по которым частные решения оказались эффективными, делается попытка построить синтетическое решение, объединяющее положительные черты частных решений. Если данная задача увенчается успехом, то будет получено эффективное решение, которое уже выходит за ограничения, налагаемые областью Парето в исходной постановке задачи.

540. Все изложенное допускает естественное обобщение на общий случай, когда задача имеет множество целевых показателей и множество ограничений. В этом случае область Парето определяется в многомерном пространстве показателей и ограничений. Задачей эффективного планирования является выбор эффективного решения из множества неулучшаемых решений. Эта задача решается на основе интерактивных процедур, включающих решение оптимизационных задач, содержательный анализ получаемых решений, коррекцию постановок задач. Эффективное решение выбирается неформально, исходя из баланса всех противоречивых условий задачи.

3.4. Управление

10. С точки зрения общей логики решения целевых задач рассмотренные в предыдущих разделах исследования, исходили из заданной объективной действительности, которая выступала в роли объекта исследования. После принятия решений направление деятельности меняется на противоположное. Возникает дуальная задача (L

s .1) – реализации принятых решений. С системной точки зрения процесс реализации решений должен быть управляемым (Ls .1. s ).

20. Полученные на предыдущей ступени исследований решения отражают идеализированный сценарий, расчетную схему которого можно представить, например, в виде (рис. 3.4.1).

209

zр

( р )

Рис. 3.4.1. Расчетная схема действий на объекте управления

На рис. 3.4.1 представлена расчетная схема действий при реализации решений. Здесь hр - расчетное значение входных воздействий на объект

управления; р - расчетное значение состояния объекта; zр - расчетное значение возмущений, yр - расчетное значение выходных результатов. Сам

объект управления здесь отражается также в виде его расчетного представления Ор.

В реальности же все рассматриваемые характеристики будут отличаться от расчетных. Формально, эти отклонения можно представить в виде

Управление призвано скорректировать объективную ситуацию, чтобы отклонения выходных результатов от расчетных были минимальными при отклонениях прочих характеристик. Формально, цель

значений характеристик.

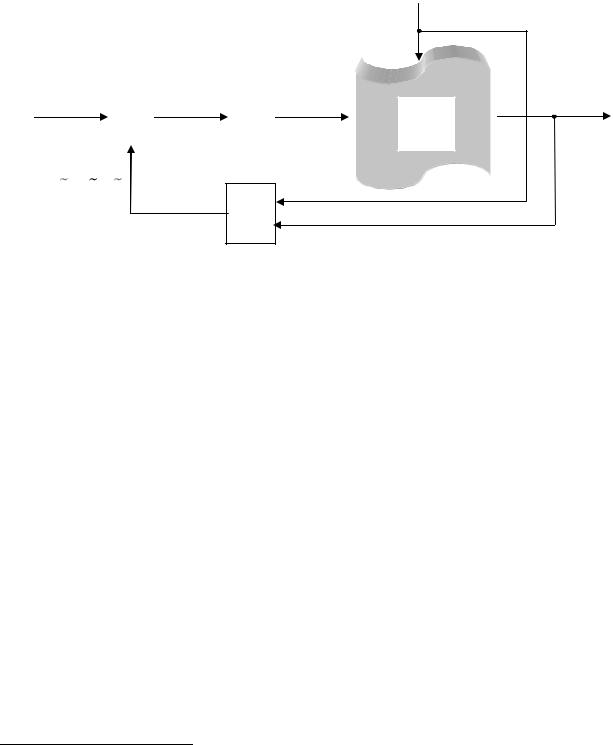
Общая схема системы управления представлена на рис. 3.4.2.

210

z

y, , z

Н

Рис. 3.4.2. Схема управления объективной ситуацией

Здесь Н – наблюдение (контроль, измерение), У – собственно управление, И – исполнение управляющих решений u 18.

Управление состоит в выработке управляющих решений, направленных на достижение целей управления в заданной объективной действительности с помощью механизма исполнения решений. Управляющие решения вырабатываются на основе наблюдения за реальной ситуацией и сравнения расчетных результатов с реальными результатами. Цель управления состоит в максимальном сближении расчетных и реальных результатов.

30. Принятие решений в процессе управления по своей постановке можно отнести к специальному классу задач исследования операций – операций по управлению объектами. Отличие их состоит в том, что процесс принятия решений здесь неразрывно связан с процессом реализации решений. Соответственно, указанный процесс связан с реальными процессами, происходящими в объекте управления и осуществляется в реальном времени.

40. Так, постановка задачи выработки управляющих решений может быть сформулирована, например, как задача модельно-упреждающего

18 Отметим, что приведенные понятия могут обозначаться в различных отраслях знаний иными терминами. Например, в биологии исполнительные органы называются эффекторы, измерительные органы – рецепторы. В англоязычной литературе исполнительный механизм называется actuator, наблюдатель – observer, управление – control.

211

управления19. Задача модельно-упреждающего управления состоит в определении управляющего воздействия на процесс, которое осуществляет его перевод в желаемый режим в рамках заданных ограничений. Управление находится из условия минимума динамической целевой функции как решение соответствующей задачи математического программирования. Решение данной задачи можно получить, например, с использованием методов, изложенных в разделе 2.5 очерка 2. Полученное решение реализуется в следующей стратегии. Задача (2) решается на каждом шаге управления при текущем горизонте планирования. В полученном решении выделяется первый следующий шаг управления и реализуется в объекте управления. При этом оценивается текущее состояние объекта и вносятся соответствующие корректирующие изменения в состояние модели объекта управления. Решение задачи итеративно повторяется на следующем шаге.

Подобная стратегия эффективно реализуется для управления объектами с относительно медленной динамикой, например, для сложных технологических процессов. Время принятия управляющих решений здесь измеряется в минутах, часах, сутках. Для быстродействующих объектов, для которых время принятия решений измеряется в миллисекундах, секундах и минутах эффективно используется иная схема выработки управляющих решений – на основе автомата, понимаемого в обобщенном смысле:

где eky – уклонение текущего значения процесса от желаемой траектории, xk – текущее состояние процесса; uk 1 – управляющее решение; R( , , ) – динамический оператор. Автомат (3) конструируется на

основе инженерных решений, решений оптимизационных задач в том числе задач модельно-упреждающего управления, если удается выразить механизм выработки управляющих решений в форме (3). Соответствующие системы управления называются системами автоматического управления.

50. Для технических объектов управление может быть реализовано в ручном и автоматическом режиме. Для автоматического режима существует следующая классификация систем автоматического управления:

–системы программного управления;

–системы автоматической стабилизации;

–системы автоматического регулирования;

–следящие системы и др.

19 Qin, S.J. A survey of industrial model predictive control technology / S.J.Qin, T.A. Badgwell // Control Engineering Practice. – 2003. – 11. – P. 733-764.

212

Всистемах программного управления используется директивный метод управления без обратной связи. Подобный подход эффективен в основном для объектов управления с детерминированной динамикой. В общем случае при воздействии возмущений используются системы с регулирующей обратной связью.

Для объектов управления, для которых основной технологической задачей является удержание режимных параметров в заданных значениях при воздействии возмущений, используются системы автоматической стабилизации с обратной связью.

Вобщем случае, когда ставится задача не только стабилизации значений режимных параметров, но и перевод технологического объекта управления с одного режима на другой, используются системы автоматического регулирования. При этом качество систем автоматического регулирования оценивается показателями переходного процесса и ошибкой стабилизации режимных параметров объекта при ступенчатом тестовом изменении задающего воздействия. Типовыми показателями качества переходного процесса являются: время регулирования, перерегулирование, наличие и частота колебаний, время запаздывания реакции и др.

Для следящих систем входной задающий сигнал может иметь произвольный вид. Задачей системы является обеспечить слежение с заданной точностью выходной реакции объекта управления за входным

сигналом.

50. Решение задач управления можно осуществлять на основе разнообразных методов. Методы решения задач управления существенно зависят от класса объектов управления. Среди методов, основанных на управлении с отрицательной обратной связью необходимо отметить:

- одноконтурное управление; - многомерное и многосвязное управление; - многоуровневое управление;

- управление в пространстве состояний; - управление с использованием обратных задач динамики; - упреждающее управление; - оперативное управление

- ситуационное управление и др.

Обзорные сведения

3.4.1. Инструктивные схемы управления

60. Правила управляющих действий можно представить лингвистически с использованием инструктивных схем. Например,

213