Т3 Логика решения задач

500. Для стратифицированного представления предмета исследования при интеллектуальном движении на верхние страты растет кругозор понимания предмета в целом. На нижних стратах растет детализация знания предмета, однако падает кругозор его понимания. Переход на верхние страты связан с агрегированием14 информации от нижних страт. В обратном направлении осуществляется дезагрегирование информации. В целом стратифицированное представление позволяет дать описание сложного предмета исследования в обозримом виде.

_____________________________________________

510. В результате предыдущих исследований формируется исходное представление о предмете исследования как о целостном единстве базовых составляющих, обладающем соответствующей структурой и функцией. Однако полученное представление отражает предмет исследования в том виде, в каком он явился исследователю, другими словами – как явление. В нем не выделены необходимые и случайные элементы. Поэтому следующий этап исследований (L1.2.s) состоит в выделении среди

составляющих полученного представления необходимых и случайных элементов, определении существенных системных связей, другими словами – системной сущности.

520. В указанном плане каждая реализация событий, действий и процессов в предметной действительности, каждая связь событий, действий и процессов должна рассматриваться с двух дополнительных друг другу точек зрения – необходимости и случайности. Необходимо то, что имеет свое основание, причину в самом предмете, что необходимо для исполнения функции предмета. Случайно то, что имеет свое основание, причину вне предмета, т.е. в другом, что не является необходимым для выполнения функции предмета. Необходимо то, что определенно должно быть, исходя из системных свойств данного предмета. Случайное же может быть, а может и не быть. В действительности необходимое и

14 Лат. aggregare – собирать в кучу, укрупнять; обратное действие – disaggregare, здесь приводится во французском варианте – désaggréger.

184

случайное связаны между собой. При этом случайное выступает как форма проявления необходимого. Логическое единство необходимого и случайного определяет возможное. Возможное проявляется в действительности в виде множества реализаций.

530. С системной точки зрения, например, при рассмотрении функциональных связей необходимыми являются входной и выходной элементы связи. Формально это можно представить, например, следующей диаграммой

элементов Y0 . При этом a0,i вследствие наличия функциональной связи G0 является достаточным условием реализации b0, j , а b0, j - необходимым следствием реализации a0,i .

В исходном множестве элементов U0 могут быть элементы, которые

не влияют на значения выхода связи. Такие элементы могут быть включены в область определения функциональной связи, а могут быть исключены. Они не являются существенными для определения связи.

Входные и выходные переменные могут представлять случайные процессы. В отличие от детерминированных процессов, реализации которых могут быть точно описаны, случайные процессы описываются обобщенными характеристиками. Например, случайные колебания могут быть описаны математическим ожиданием, дисперсией, энергетическим спектром. При этом фазовые характеристики процессов не являются необходимыми для представления процессов.

540. В сложных системах все элементы соединены между собой цепочками связей, которые могут быть последовательными, разветвляющимися и циклическими. В циклических связях каждый элемент выступает с одной стороны, как исходное значение аргумента функциональной связи, с другой стороны он является необходимым следствием значений аргумента другой связи, соединенной с ним. Таким образом элементы, которые участвуют в циклических связях являются необходимыми и системно обоснованными. При этом разомкнутые связи определяют внешние воздействия на систему, которые в общем случае исходят либо от среды, либо являются результатом активного воздействия

185

со стороны лиц, осуществляющих управление системой. Воздействия среды, как правило, являются случайными.

550. С учетом случайного в действительности реализуются, например, связи следующей структуры

алгебраическая операция сложения, которая, например, для каждого

случайностей, но и от внутреннего состояния предмета. В этом случае системная связь будет иметь вид

где - переменная состояния предмета, – случайная составляющая состояния.

570. В целом системный подход исходит из постулата взаимосвязи всех явлений действительности. Это приводит к рассмотрению многоконтурных связей исследуемых предметов. Как уже отмечалось, системное мышление - это прежде всего контурное мышление, которое исследует прямые и обратные связи действительности. В этом плане любое событие, действие или процесс не просто выступают исходным пунктом, причиной изменений других событий и процессов, связанных с ними. Находясь в контуре обратной связи, они одновременно выступают необходимыми следствиями этих и других событий и процессов, являются обоснованными ими. В этом состоит системное понимание рассматриваемой действительности.

580. Наблюдаемые явления содержат случайные составляющие. Однако за ними стоят системные связи, которые придают явлению необходимые характеристики. В общем случае сами системные связи также могут носить случайный характер и меняться от реализации к реализации. Поэтому необходимо раскрывать существенные связи, которые устойчиво определяют причины происходящих явлений. Совокупность указанных связей образует системную сущность рассматриваемых явлений.

590. Для сложных предметов исследования системная сущность носит многоуровневый характер. В этом случае различается сущность первого порядка, просматриваемая при первом рассмотрении предмета исследования, далее сущности второго и более высокого порядка, отражающие более глубокое изучение событий, процессов и явлений действительности. В этой иерархии сущностей в качестве сущности

186

нулевого порядка можно принять явление, как поверхностное отражение предмета.

Знание системной сущности наблюдаемых событий, действий, процессов и явлений создает основу их системно-аналитического понимания.

___________________________________________

600. Следующей ступенью развития исследований (L1. s ) является системный анализ рассматриваемой предметной действительности. Исходным пунктом (L1. s .1) здесь является построение системных

представлений о предметах исследования на основе систематизации всех ранее полученных знаний.

610. Первым этапом построения системных представлений является составление перечней всех возможных альтернатив развития событий, действий, процессов и явлений рассматриваемой предметной действительности, а также возможных значений их параметров и показателей.

620. Используя язык теории множеств, указанные перечни можно представить в виде следующих множеств:

- множеств i возможных альтернатив внутренних состояний предметов исследования

{ 1, 2 , 3 . . . };

- множеств Ui возможных альтернатив внешних воздействий на предметы исследования

{U1, U2 , U3 . . . };

- множеств Zi возможных альтернатив случайных воздействий

{Z1, Z2 , Z3 . . . };

- множеств Yi возможных альтернатив выходных реакций предметов

исследования

{Y1, Y2 , Y3 . . . }

и др.

630. Перечисленные множества определяют первичную информацию о предметах исследования. Вторичную информацию дают показатели

y Y1 Y2 . . .

Возможные значения показателей, как правило, образуют упорядоченные множества оценок

pi Pi {{ci, j : j Iic }; >},

187

640. На следующем этапе исследования необходимо составить

перечни всех отношений и функций, определяющих системные связи рассматриваемых предметов. На языке теории множеств указанные перечни формализовано представляются в виде следующих множеств:

- предикатов, выражающих отношения,

{R1, R2 , R3 . . . };

- функций, определяющих функциональные связи,

{F1, F2 , F3 . . . }.

Предикаты и функции в общем случае определяются на всех переменных, описывающих предмет исследования

где функции Fi определены неявно.

650. На заключительном этапе приведение в единую систему всех рассмотренных составляющих позволяет получить формализованное

системное представление о предметах исследования

... .

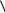660. В общем случае системное представление носит иерархический многоуровневый характер. Такой подход позволяет дать обозримое описание сложных предметов исследования.

________________________________________________

670. Построенные системные представления используются в дальнейшем для решения задач системного анализа. Среди задач системного анализа будем выделять два класса – прямые и обратные задачи.

680. Прямые задачи состоят в вычислении значений предикатов и функций, заданных в явном виде. Здесь значения аргументов предикатов и функций считаются заданными, а соответствующие значения предикатов и функций – неизвестными. Формально это можно представить в следующем виде:

x a, p(x) ? , x a, f (x) ? ,

где p(x) - предикат, f (x) - функция, x - исходный аргумент, в роли которого могут быть использованы самые различные характеристики исследуемого предмета.

Для решения указанных задач необходим метод, который бы за конечное число шагов вычислительных операций, приводил бы к

188

искомому решению, т.е. к вычислению значения предиката p(x) и функции f (x) .

690. Понятие вычисление здесь понимается в предельно общей трактовке, как это принято в математической логике - с включением дедуктивных операций. Действительно, в математической логике разрешающим методом для некоторой формализованной теории Th называется такой метод, с помощью которого для любой данной формулы из Th мы можем за конечное число шагов решить, будет ли она истинной в Th или нет. Очевидно, что данная задача сводится к вычислению истинностного значения формулы, записанной в общем случае в виде предиката.

Сам разрешающий метод в математической логике понимается как некоторый механический метод, который приводит к искомому решению задачи за конечное число шагов на основе элементарных вычислительных операций. Проблема разрешимости для поставленных задач состоит в следующем: найти разрешающий метод для указанных задач, либо доказать, что такого метода не существует.

700. Прямые задачи отражают, как правило, последовательные системные связи предметов исследования. Например, это могут быть задачи прогноза следствий какого-либо явления. Нахождение метода вычисления последовательных системных связей составляет одну из основных задач системного анализа.

710. Для обратных задач – решений уравнений и неравенств, наоборот, значения предикатов и функций заданы. Здесь необходимо определить соответствующие значения аргументов:

В общем случае обратные задачи являются недоопределенными и характеризуются множествами допустимых решений. Поэтому методы решения задач здесь должны вычислять не единичные решения, а множества допустимых решений.

720. Обратные задачи возникают в системном анализе, например, при рассмотрении замкнутых контуров системных связей. Так, типичным уравнением здесь будет уравнение вида

x f (x) .

Его можно привести к стандартному виду

f (x) x 0 .

Обратим внимание также, что системы уравнений, которые описывают системные связи, составленные на основе структуры предмета исследования, как правило, выражаются в неявном виде относительно выходных реакций. Это также приводит к необходимости решения соответствующих обратных задач.

189

730. К обратным задачам приводят также задачи, в которых ставится выяснение причин какого-либо наблюдаемого явления.

740. В общем случае при решении задач системного анализа методы решения представляют собой композицию частных методов решений прямых и обратных задач, отражающую структурные и функциональные свойства системных представлений. Такие методы, как правило, являются итерационными. Важным свойством итерационных методов является их

сходимость.

750. Общую схему итерационных методов можно представить рекуррентной формулой

где k - шаг вычислений.

Рекуррентная формула порождает последовательность x0 , x1 , x2 , ..., xi , ...

Для оценки сходимости данной последовательности, необходимо дать формальное определение расстояния между ними.

760. Например, с этой целью на множестве X значений переменных можно ввести меру расстояния – метрику: ( xi , x j ) , определенную для

любых элементов xi , x j из множества X и удовлетворяющую условиям:

1)( xi , x j ) = 0 тогда и только тогда, когда xi x j ;

2)(аксиома симметрии): ( xi , x j ) = ( x j , xi ) ;

3)(аксиома треугольника): ( xi , xl ) ( xi , x j ) ( x j , xl ) .

При этом пара X , называется метрическим пространством.

770. Рекуррентная последовательность сходится, если выполняется условие

lim (xk , xk 1 ) 0 .

k

Если метрическое пространство полное, то рекуррентная последовательность сходится к элементу xp - решению уравнения

xp (xp ) .

780. В общем случае метод решения представляет собой сложную композицию итерационных процессов.

790. Исследование на данном этапе (L1. s .2) состоит в выборе

подходящих методов для решения поставленных задач системного анализа.

__________________________________________

800. Рассмотренные выше системные представления являются формализованными структурами, выражающими системные знания о предметах исследования. Применение вычислительных операций к

190

указанным структурам, понимаемым в самом общем смысле, включающем аналитические и собственно вычислительные методы, позволяет построить вычислительные модели (L1. s.s ), с помощью которых можно решать

разнообразные задачи системного анализа. Таким образом, вычислительная модель выступает как логическое единство формализованных системных представлений и методов решения задач системного анализа.

810. Прямой задачей системного анализа является задача прогноза следствий. Решение задачи прогноза следствий с использованием вычислительных моделей состоит в задании исходных данных о входных воздействиях на модели исследуемого объекта и последующем вычислении реакций этого объекта и соответствующих показателей качества.

820. Обратной задачей системного анализа является выяснение на вычислительной модели возможных причин наблюдаемых событий, действий, процессов и явлений предметной действительности. Здесь информация о наблюдаемых событиях, действиях, процессах и явлениях выступает в виде исходных данных для решения рассматриваемой задачи. Результатами решения являются данные о возможных причинах указанных событий, действий, процессов и явлений.

830. В целом результаты решения прямых и обратных задач системного анализа формируют системно-аналитическое представление о

предметах исследования или, другими словами, его системноаналитическое понимание. Владение системно-аналитическим пониманием предмета позволяет лицу, проводящему исследование, обосновано отвечать на вопросы по существу рассматриваемого предмета.

3.3 Принятие решений

10. После того, как получены необходимые знания в предметной области, следующей ступенью (L2) развития интеллектуального процесса

достижения генеральной целевой установки является формирование,

анализ и выбор конкретного плана действий. Начальным этапом (L2.1)

решения указанной задачи является анализ целей.

20. Анализ целей осуществляется в рамках категорий «цель– средство». Указанные категории являются двойственными по отношению к категориям «причина–следствие». Разница между ними состоит в том, что категории «причина–следствие» выражают причинно-следственные связи объективной действительности. В то время как категории «цель– средство» выражают целенаправленные связи субъективного процесса

191

деятельности. Для обеспечения эффективности деятельности необходимо, чтобы цели соответствовали объективным следствиям, а средства – объективным причинам. Тогда применение средств в объективной действительности приведет к следствиям, соответствующим целям.

Представляет интерес отметить, что в средневековой философии различались causae efficientes (действующие причины) и causae finales (конечные причины). Конечные причины суть цели, для которых действующие причины суть средства.

30. Основываясь на данных общих положениях, можно утверждать, что владение системно-аналитическими знаниями в предметной области позволяет лицу, проводящему исследования, исходя из целей деятельности, указывать средства их достижения.

Исходным пунктом анализа целей является постановка генеральной цели в соответствии с генеральной целевой установкой. Генеральная цель в общем случае определяет желаемую ситуацию 0 в рассматриваемой

объективной действительности, которую ЛПИ хочет получить. Далее, исходя из генеральной цели, ЛПИ должен указать непосредственные средства, на основе которых может быть достигнута генеральная цель. В общем случае указанные средства могут быть недоступными, поэтому они должны рассматриваться как частные цели 1, 2 , 3 , ... нижнего уровня.

Для каждой частной цели могут быть определены свои средства – далее, процесс развертывания целей и средств итеративно повторяется. Процесс развертывания целей и средств заканчивается на средствах 1, 2 , 3 , ...,

которые доступны для непосредственного применения15. В общем случае частные цели и средства образуют множества альтернативных вариантов.

40. Результат развертывания целей и средств можно представить в виде структуры, приведенной на рис. 3.3.1. Здесь ik - частные цели, принадлежащие l -ому уровню иерархии целей ( i Il , где Il - множество

значений индексов i , принадлежащих l -ому уровню). Индекс k характеризует альтернативные цели, образующие i -ые множества

15 Принцип развертывания целей и средств был сформулирован английским философом Томасом Гоббсом (1588-1679) в знаменитом сочинении «Левиафан» (1651): «От желания возникает мысль о некоторых средствах, при помощи которых мы видим осуществленным нечто подобное тому, к чему мы стремимся, и от этой мысли – мысль о средствах для достижения этих средств и так далее, пока мы не доходим до некоторого начала, находящегося в нашей собственной власти». Интересно отметить, что в указанном сочинении Гоббса центральной мыслью, сделавшей его знаменитым, является утверждение, что человек по своей естественной сути эгоистичен, но подчиняется общественному договору (между людьми) для создания цивилизованного общества. Государство, которое Гоббс уподобляет мифическому библейскому чудовищу Левиафану, - результат договора между людьми, положившему конец естественному состоянию «войны всех против всех».

192

альтернативных целей Hi . Множества альтернативных целей Hi связаны между собой отношениями типа «цель – средство». Аналогичным образом

альтернативных средств i , которые связаны с целями более высокого

уровня отношениями типа «цель–средство». В итоге, структура (рис. 3.3.1) выражает связи «цель–средство» в логических связках «И–ИЛИ (разделительное)».

50. Обратим внимание, что процесс развертывания структуры «цель– средство» представляет собой обратную задачу системного анализа. Указанные задачи в общем случае являются недоопределенными, поэтому характеризуются множествами альтернативных решений. Этим объясняется наличие альтернативных средств в структуре (рис. 3.3.1). Указанное свойство обратных задач является принципиальным при выборе решений. Обратные задачи системного анализа по своей логике имеют множество альтернативных решений. Произвольный выбор в качестве решения одного из допустимых противоречит принципам системного подхода. При решении целевых задач необходимо выявить полное множество всех возможных альтернативных решений, после чего необходимо сделать обоснованный выбор наиболее эффективного решения.

60. Процесс развертывания структуры «цель–средство» аналогичен процессу выдвижения идеи достижения генеральной целевой установки. Отличие состоит в том, что идея выдвигается при более низком уровне знаний в рассматриваемой предметной области и поэтому является более абстрактной. Напротив, развертывание структуры «цель–средство» происходит уже на фоне имеющегося опыта решения соответствующих обратных задач системного анализа и поэтому является более конкретным.

193