Т3 Логика решения задач

Здесь Emp{} - эмпирический базис задачи идентификации, состоящий из множества данных наблюдений (xs , zs , ys ) : s Is ; QI ( ) - интегральный

показатель невязки решения задачи идентификации на множестве данных; QL ( ) - интегральный показатель невязки решения задачи выделения

области компетенции эмпирической зависимости y f (c; x, z) .

130. В результате решения задачи идентификации Id ( ) будут получены значения структурных параметров c0 и d0 ограничений Mod0 ( ) , Loc0 ( ) , что дает возможность поставить задачу Opt0{}. Далее, на основе

решения поставленной оптимизационной задачи (см. раздел 3.3) определяется расчетное значение вектора режимных параметров объекта xp,0 . Полученное значение xp,0 передается как расчетное в систему

управления нижнего уровня (см. раздел 3.4). Если найденное значение вектора режимных параметров xp,0 находится внутри области

компетенции Loc0 ( ) задачи Opt0{}, то xp,0 принимается как оптимальное, и решение поставленной задачи считается законченным. Если xp,0 находится вне области компетенции Loc0 ( ) , то подобное решение xp,0 и сама задача Opt0{} считаются локальными. Для улучшения полученного решения формируется новая область исследований Loc1 ( ) , которая включает в себя как внутреннюю точку значение вектора xp,0 (например, в

качестве центральной точки области). В новой области исследований Loc1 ( ) снова решается задача идентификации Id1 ( ) . В результате будут

получены новые модельные соотношения Mod1 ( ) , для которых указанная область Loc1 ( ) будет уже исполнять роль соответствующей области компетенции. Далее ставится задача Opt1{}, в результате решения которой находится оптимальное решение xp,1 . Процесс решения итеративно

повторяется.

Рассмотренный процесс поиска оптимального решения представляет собой процесс экспериментальной оптимизации. Задача экспериментальной оптимизации состоит из итеративного решения следующих подзадач: идентификации Id ( ) , оптимизации Opt( ) и

реализации решений. При этом на шаге k решения задачи экспериментальной оптимизации сначала решается локальная подзадача идентификации Idk ( ) . В результате решения задачи Idk ( ) определяются

текущие значения структурных параметров ck и dk . Далее решается локальная подзадача оптимизации Optk {}. На ее основе определяется текущее расчетное значение вектора параметров xp,k . В зависимости от

294

того, находится ли расчетное значение xp,k внутри или вне области

компетенции решаемой локальной задачи, оно принимается как оптимальное или локальное. Полученное решение реализуется на практике.

В целом описанная схема поиска оптимального решения представляет собой метод крутого спуска (при использовании функций качества – крутого восхождения).

140. В рассматриваемой задаче процесс поиска оптимального решения можно ускорить, если после нахождения двух локальных решений процесс поиска продолжить в частном перспективном

где - величина шага в частном перспективном направлении поиска.

где x( ) определяется соотношением (1.22).

После нахождения оптимального решения в частном перспективном направлении:

xp,k 1 (1 opt )xp,k 1 opt xp,k , 1, (1.24)

снова решается задача (1.20). В результате будет получено новое решение xp,k 2 . Пара решений xp,k 1 , xp,k 2 образуют новое перспективное

направление поиска решений согласно соотношению (1.22). Процесс поиска решения итеративно продолжается. Если рассматриваемый процесс сойдется, то в результате будет получено оптимальное решение. Рассмотренный метод поиска оптимального решения называется методом наискорейшего спуска (подъема).

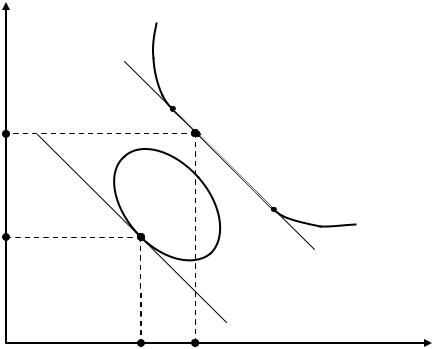
150. В общем случае рассмотренные методы экспериментальной оптимизации позволяют находить лишь локальные экстремумы решаемой экстремальной задачи. Их сходимость обусловлена нахождением в области «притяжения» локального экстремума. Фактически, данные методы осуществляют количественное уточнение качественно полученного исходного решения. Суть проблемы решения многоэкстремальных оптимизационных задач можно проиллюстрировать графически (см.

рис. 3.6.1).

160. На рис. 3.6.1 тонкими линиями обозначены линии уровня целевой функции, нахождение экстремальных значений которой составляет цель решения задачи оптимизации.

x0i

Из рисунка (3.6.1) видно, что для рассматриваемого примера существуют три различных локальных экстремума. Задача состоит в нахождении среди них глобального экстремума, который превосходит остальные по экстремальному значению целевой функции.

Предположим, что процесс поиска экстремальных значений целевой функции основывается на использовании метода наискорейшего спуска, который относится к классу градиентных методов. В этом случае траектория поиска решения ориентируется перпендикулярно линиям уровня целевой функции в направлении ее возрастания или убывания.

На рисунке (3.6.1) представлены различные траектории поиска экстремумов в зависимости от исходных точек процесса решения. Так, при поисковом движении из точки x0 процесс вначале идет по направлению к

точке x1 . Точка x1 представляет собой точку бифуркации поискового

процесса. Здесь влияние двух ближайших экстремумов компенсировано и вследствие случайных флюктуаций процесс поиска может пойти как по направлению к точке x2 , так и по направлению к точке x3 . В результате

будут найдены два различных локальных экстремума. Третий экстремум будет найден, если решающий процесс пойдет из совершенно другой точки - x0i . Таким образом, рассмотренный градиентный метод позволяет

выделить лишь локальные экстремумы.

170. Существует множество методов поиска глобального экстремума. Наиболее простой из них – метод Монте-Карло. Метод Монте-Карло

296

состоит в том, что в заданной области поиска решений случайным образом генерируется множество исходных точек поиска {x0i }. Далее, из каждой

точки x0i осуществляется поиск соответствующей локальной экстремальной точки xm,i . Из всех локальных экстремальных точек {xm,i }

в качестве решения выбирается та, которая обладает наибольшим (наименьшим) экстремальным значением целевой функции. Различные модификации метода Монте-Карло составляют обширный класс алгоритмов случайного поиска решений многоэкстремальных задач.

Недостатком метода Монте-Карло является то, что исходные варианты решений генерируются случайно. Среди них может быть множество вариантов, не имеющих технического смысла. Подобные варианты решений повышают трудоемкость поиска, особенно в задачах экспериментальной оптимизации.

180. В технических задачах варианты решений генерируются либо на основе инженерного опыта и интуиции, либо на основе решения задач исследования операций, либо иными способами. Одним из универсальных подходов к сокращению перебора вариантов здесь является метод ветвей

играниц.

Впростейшем случае метод ветвей и границ исходит из некоторого набора исходных вариантов допустимых решений {x0i }0 . Такой набор

вариантов может быть получен, например, на основе решения задач исследования операций. Для каждого варианта решения определяются, тем или иным образом, оценки ожидаемого экстремального значения целевой

функции {pm,i }. Из всех возможных вариантов выбирается наиболее

перспективный вариант, который имеет наибольшее (наименьшее) значение целевой функции:

Решая задачу оптимизации в перспективном k -ом варианте (с возможной реализацией на практике), можно получить для данного

варианта реально достигнутое значение целевой функции pmr ,k . Зная

достигнутое значение целевой функции (текущий рекорд) pmr ,k , из множества допустимых вариантов решений {x0i }0 отсеиваются те варианты, ожидаемые экстремальные значения целевой функции pm,i для

вариантов поиска решений {x0i }1 . Для полученного набора вариантов {x0i }1 описанная процедура поиска решения итеративно повторяется.

297

Процесс поиска решения заканчивается после получения реальных значений целевой функции по всем перспективным вариантам поиска решений. В качестве оптимального решения в глобальном смысле принимается решение с рекордным значением целевой функции.

В общем случае метод ветвей и границ основывается на многоуровневом представлении вариантов решения экстремальных задач.

Критическим моментом при решении переборных многоэкстремальных задач является генерация и селекция приемлемых вариантов решений. В данном направлении одним из перспективных подходов является использование генетических алгоритмов.

3.6.2. Генетические алгоритмы

190. Генетические алгоритмы моделируют естественные эволюционные процессы и на этой основе имитируются процессы адаптации и селекции в автоматизированных системах. Рассмотрим характерные особенности генетических алгоритмов.

200. Первым шагом в понимании естественных эволюционных алгоритмов явилась работа Чарльза Дарвина «Происхождение видов», написанная в 1859 году. Именно в этой работе четко обозначены три принципа, на которых основываются современные генетические алгоритмы, – наследственность, изменчивость и отбор. Однако, если отбор - процесс отбраковки нежизнестойких видов, был описан, то механизм, который отвечал за сохранение в потомках черт предков и обеспечивал способность к приспособлению под новые условия окружающей среды, был выявлен гораздо позднее. В 1944 году О. Эйвери, К. Маклеод и М. Маккарти опубликовали результаты своих исследований, которые доказывали, что за наследственные процессы ответственна «кислота дезоксирибозного типа». Однако о том, как работает ДНК, было выяснено позднее – 27 апреля 1953 года в номере журнала «Nature» вышла статья Уотсона (Watson J.D. ) и Крика (Crick F.H.), впервые предложивших модель двухцепочечной спирали ДНК.

210. Раскрытие механизмов, отвечающих за создание и работу таких сложных систем, как живые организмы, вдохновило многих исследователей на моделирование этих процессов при помощи компьютеров. В настоящее время существует огромное количество различных алгоритмов, в той или иной степени моделирующих естественные процессы. В качестве основных направлений можно назвать генетические алгоритмы и классификационные системы Голланда

298

(Holland, J.H.)42, опубликованные в начале 60-х годов и получившие всеобщее признание после выхода в свет книги «Адаптация в естественных и искусственных системах», ставшей классикой в этой области. В 70-е годы Л.А. Растригиным в рамках теории случайного поиска был предложен ряд алгоритмов, которые моделировали различные аспекты поведения живых организмов. Дальнейшее развитие эти идеи получили в работах Букатовой И.Л., посвященных эволюционному моделированию. Развивая идеи Цетлина М.Л. о целесообразном и оптимальном поведении стохастических автоматов, Неймарк Ю.И. предложил осуществлять поиск глобального экстремума на основе коллектива независимых автоматов, моделирующих процессы развития и элиминации особей. Большой вклад в развитие эволюционного программирования внесли Л. Фогел (Fogel L.J.) и М. Уолш (Walsh M.J.). При всей разнице в подходах каждая из этих научных школ, взяв за основу ряд принципов, существующих в природе, упростила их до такой степени, чтобы их можно было реализовать на компьютере в виде вычислительной модели.

220. Рассмотрим особенности построения генетических алгоритмов. Генетические алгоритмы (ГА) являются самыми известными на

данный момент представителями эволюционных алгоритмов и по своей сути являются алгоритмами для нахождения глобального экстремума многоэкстремальной функции.

В этой связи рассмотрим целую функцию от многих переменных, у которой необходимо найти глобальный максимум или минимум:

f x1, x2 , x3,..., xn .

Для того чтобы применить ГА, необходимо представить независимые переменные в виде хромосом – цепочек символов, с которыми и работают ГА.

На первом шаге независимые переменные преобразуются в цепочки бит, которые будут содержать всю необходимую информацию о каждой создаваемой особи. Имеется два варианта кодирования параметров:

-в двоичном формате;

-в формате с плавающей запятой.

В случае двоичного кодирования используются N бит для каждого параметра, причем N может быть различным для каждого параметра.

230. В общем случае, генетические алгоритмы·работают следующим образом. В первом поколении задается исходная популяция особей либо все хромосомы генерируются случайно. Определяется их «полезность» на

42 Holland, J. Adaptation in natural and artificial systems / J. Holland. – Cambridge:

MIT Press, MA, 1992.

299

основе некоторой оценочной функции. Начиная с этой точки, ГА может начинать генерировать новую популяцию. Обычно размер популяции постоянен.

Репродукция состоит из двух шагов:

1.Селекции.

2.Генетических операторов (порядок применения не важен), из которых самыми важными и принципиально необходимыми являются:

- кроссовер; - мутация.

240. Кроссовер является наиболее важным генетическим оператором. Он генерирует новую хромосому, объединяя генетический материал двух родительских. Существует несколько вариантов кроссовера. Наиболее простым является одноточечный. В этом варианте просто берутся две хромосомы и перерезаются в случайно выбранной точке. Результирующая хромосома получается из начала одной и конца другой родительских хромосом:

001100101110010|11000 → 00110010111001011100 110101101101000|11100

250. Мутация представляет собой случайное изменение хромосомы (обычно простым изменением состояния одного из битов на противоположное). Данный оператор позволяет более быстро находить локальные экстремумы, так как он дает возможность «перескочить» с одного локального экстремума на другой:

00110010111001011000 → 00110010111001111000

260. Примером дополнительных операторов может служить инверсия. Инверсия изменяет порядок бит в хромосоме путем циклической перестановки (случайное количество раз). Многие модификации ГА обходятся без данного генетического оператора:

00110010111001011000 → 11000001100101110010

270. Представляется интересным вопрос: почему ГА на несколько порядков превосходят по скорости случайный поиск во многих задачах? Дело здесь, видимо, в том, что «большинство систем имеют довольно независимые подсистемы. Вследствие этого при обмене генетическим материалом часто может встретиться ситуация, когда от каждого из родителей берутся гены, соответствующие наиболее удачному варианту определенной подсистемы (неудачные варианты систем постепенно вымирают). Другими словами, ГА позволяют накапливать удачные решения для систем, состоящих из относительно независимых подсистем (какими являются большинство современных сложных технических систем и все известные живые организмы). Соответственно, можно предсказать и когда ГА скорее всего даст сбой (или, по крайней мере, не покажет особых преимуществ перед методом Монте-Карло), – системы,

300

которые сложно разбить на подсистемы (узлы, модули), а также в случае неудачного порядка расположения генов (рядом расположены параметры, относящиеся к различным подсистемам), при котором преимущества обмена генетическим материалом сводятся к нулю».

280. Другим важным моментом, которым отличаются различные генетические алгоритмы, является процесс селекции. Здесь используются и простой допуск к размножению определенного количества лучших объектов, и сложные турнирные схемы, элитизм (дарование жизни самым лучшим особям – элите, и в следующем поколении), разделение популяции на несколько частей с нечастыми обменами генетическим материалом между ними и др.

В целом генетические алгоритмы представляют в настоящее время одно из перспективных направлений исследований процессов самоорганизации в сложных системах управления.

3.6.3. Методы адаптации и самоорганизации на основе решения целевых неравенств

290. Использование целевых неравенств представляет собой одно из перспективных направлений исследований, связанных с процессами адаптации и самоорганизации в автоматизированных системах управления.

Принципиальные идеи, связанные со снятием ограничений в интерактивных процессах оптимизации, развивались академиком В.М. Глушковым43 в виде концепции «системной оптимизации». Данный

проектирования сложных систем управления. Математический аппарат нестационарных процессов математического программирования, ориентированный на решение задач в противоречивой постановке, получил развитие в работах И.И. Еремина и В.Д. Мазурова45.

43Глушков, В.М. О диалоговом методе решения оптимизационных задач / В.М. Глушков // Кибернетика. – 1975. – № 4.

44Михалевич, В.С. Вычислительные методы исследования и проектирования сложных систем / В.С. Михалевич, В.Л. Волкович. – М.: Наука. Главная редакция физико-математической литературы, 1982.

45Еремин, И.И. О несовместных системах линейных неравенств. – ДАН СССР. – 1961. – 138

Мазуров, В.Д. О построении комитета системы выпуклых неравенств / В.Д. Мазуров // Кибернетика. – 1967. – № 2.

Еремин, И.И. Нестационарные процессы математического программирования / И.И. Еремин, В.Д. Мазуров. – М.: Наука. Главная редакция физико-математической литературы, 1979.

301

Применительно к задаче распознания образов здесь следует отметить работы К. Эйблау и Д. Кэйлора46, Л.А. Расстригина, Р.Х. Эренштейна47. Для адаптивных систем управления подход на основе решения рекуррентных целевых неравенств развивался в работах В.А. Якубовича 48. Управлению качеством промышленных изделий на основе распознания образов посвящена работа Л.И. Тягунова, Э.Г. Карапетяна, Р.Г. Мирзоева49 и др.

300. Решение задач адаптации и самоорганизации на основе использования целевых неравенств в дальнейшем будем называть обобщенно как метод целевых ограничений, или сокращенно – метод ограничений. Основную идею метода ограничений можно иллюстрировать следующим образом.

Предположим, ставится задача найти условный минимум показателя

где - неопределенный множитель Лагранжа. Решение находится на основе безусловной минимизации функции Лагранжа. При этом неопределенный множитель Лагранжа определяется из условия удовлетворения решением заданного ограничения. Как было показано ранее (см. раздел 3.3, рис. 3.3.2), искомое решение лежит в области Парето - области неулучшаемых решений. Множитель Лагранжа определяет асимптоту, проведенную к области Парето в точке решения.

В случае сложной конфигурации области Парето рассматриваемая ситуация выбора решения значительно усложняется. В качестве иллюстрации на рис. 3.6.2 представлен пример области Парето сложной конфигурации.

Рассматриваемая область является несвязной и разделена на две

определенное решение. Здесь весь линейный участок A C представляет собой множество оптимальных решений, так как функция Лагранжа на

46 Ablow, C.M. Inconsistent homogeneous linear inequalities / C.M. Ablow, D.J. Kaylor // Bul. Amer. Math. Soc. – 1965. – 71. – № 1.

47Расстригин, Л.А. Метод коллективного распознания / Л.А. Расстригин, Р.Х. Эренштейн. – М.: Энергоиздат, 1981.

48Якубович, В.А. Рекуррентные конечно-сходящиеся алгоритмы решения систем неравенств / В.А. Якубович // Доклады АН СССР. – 1966. – Т. 166. – № 6. – С.

1308-1311.

Якубович, В.А. К теории адаптивных систем / В.А. Якубович // Доклады АН

СССР. – 1968. – Т. 182. – № 3. – С. 518-521.

49Тягунов, Л.И. Управление качеством промышленных изделий / Л.И. Тягунов, Э.Г. Карапетян, Р.Г. Мирзоев. – Л.: Изд-ство Ленингр. ун-та, 1977. – 120 с.

302

этом участке будет постоянной, хотя составляющие ее показатели могут менять свои значения. Решаемая задача имеет множество экстремумов.

p1

p1,D p1,B

Рис. 3.6.2. Выбор решений методом ограничений при сложной конфигурации области Парето

Решение для той же задачи, но на основе метода ограничений, находится путем решения соответствующих целевых неравенств:

- для экстремальной точки B

p1 (x) p1,B , p2 (x) p2,B ;

- для экстремальной точки D

p1 (x) p1,D , p2 (x) p2,D .

Очевидно, что проблем, связанных с локализацией точек решения относительно области Парето, здесь не возникает. Все проблемы перемещаются в решение соответствующих систем целевых неравенств.

310. В этой связи необходимо отметить, что инженерные показатели качества технических систем неслучайно формулируются в виде ограничений – технических условий. Ограничения позволяют точно определить требуемое качество системы, достижение же заданного

303