Т3 Логика решения задач

6 зависимыми согласно соотношениям (4.11). В этом случае в качестве плана эксперимента можно использовать таблицу 3.5.4. Число

где n - общее число переменных, m - число зависимых переменных. Изложенный материал допускает обобщения и на более общие случаи.

270. Обратим внимание, что задача построения эмпирических зависимостей является разрешимой и максимально упрощается при ортогональном плане эксперимента (см. таб. 3.5.4). При этом действующие факторы принимают граничные значения {+, -}. В общем плане интерпретация данного факта состоит в том, что для повышения эффективности процесса познания необходимо рассматривать крайние точки – противоположности, которые в совокупности позволяют выявить с достаточной полнотой свойства объекта исследования и раскрыть их системные связи.

____________________________

280. Рассмотренная выше методика ортогонального планирования эксперимента позволяет выявить линейные влияния факторов на выходной эффект, а также взаимодействие факторов. Однако данная методика не позволяет выявить нелинейные влияния факторов, такие как – квадратичные, кубические и т.п. В этих случаях необходимо использовать более общие подходы к планированию экспериментов, например,

композиционное планирование.

290. В общем случае композиционное планирование осуществляется в два этапа.

На первом этапе осуществляется анализ частных зависимостей, которые входят как составляющие в состав конкретной исследуемой зависимости. Отличие частных зависимостей от искомой состоит в том, что они выделяют лишь определенные аспекты связей объекта исследования. Соответственно частные зависимости определяются, как правило, при вариациях переменных, присущих исследуемому аспекту объекта, и при постоянных значений других переменных. Такой подход значительно упрощает исследование объекта, позволяет представить рассматриваемые зависимости в обозримом виде, а также интерпретировать их в рамках предметных теорий.

Среди частных зависимостей целесообразно выделять базовую зависимость и уточняющие зависимости. Базовая зависимость отражает

264

упрощенную модель объекта исследования в целом и представляет в определенном смысле существенные характеристики процессов, происходящих в объекте исследования. Например, для пиротехнологических процессов такими характеристиками являются характеристики процессов горения. Соответственно, упрощенная модель этих процессов может служить в качестве базовой зависимости. Уточняющие зависимости отражают частные характеристики, представляющие определенные частные аспекты объекта исследования.

Обозримость частных зависимостей позволяет представлять их в наглядном виде, в осмысленных формулах и достаточно просто определять экспериментально. Планирование экспериментов здесь осуществляется, исходя из конкретных особенностей частных зависимостей. Например, частный план исследования квадратичной зависимости y ai i2 имеет вид

кубической зависимости y ai i3

В общем случае частные зависимости могут иметь более сложный характер и содержать несколько переменных. В этом случае планы экспериментов составляются для соответствующих базовых переменных.

300. На втором этапе решения рассматриваемой задачи осуществляется композиция частных зависимостей в одну комплексную зависимость. При этом целесообразно учесть следующие условия:

–частные зависимости должны следовать из комплексной зависимости при фиксации значений коэффициентов при переменных, которые не входят

всостав соответствующей частной зависимости;

–комплексная зависимость в общем случае должна включать дополнительные уточняющие переменные, а также их взаимодействия.

План экспериментов по определению комплексной зависимости определяется на основе композиции следующих планов:

–факторный эксперимент 2n m ;

– планы экспериментов { k } для определения частных зависимостей.

Композиционный план экспериментов в общем случае не является ортогональным. Поэтому решение задачи определения комплексной зависимости выполняется на основе общего подхода, рассмотренного в п. 3.5.2. При этом в качестве регуляризующих используются значения коэффициентов частных зависимостей, полученных на первом этапе исследований.

310. Формально определение комплексной зависимости с использованием метода регуляризации можно представить, как решение экстремальной задачи

где Eс2 (a) – среднеквадратическая ошибка комплексной зависимости на

составе двух этапов: (10) выбор оптимального значения вектора структурных параметров a по критерию минимума среднеквадратической ошибки комплексной зависимости на обучающих данных, (20) выбор оптимального

постановка задачи будет без регуляризации и ее решение в общем случае неустойчивым; при R 1 решение задачи дает известные частные

зависимости, детально рассмотренные на первом этапе исследований. Промежуточные значения параметра регуляризации позволяют учесть в комплексной зависимости результаты исследований частных зависимостей, что является необходимым условием корректной постановки общей задачи

(4.15).

320. Рассмотрение зависимостей выходных эффектов от входных факторов производилось выше в предположении, что входные факторы являются независимыми переменными. В общем случае данное предположение не выполняется и значения входных факторов могут принадлежать сложным областям допустимых значений. Построение границ подобных областей на основе экспериментальных данных может быть выполнено на основе различных подходов. Так, например, подобные задачи формально могут быть сведены к уже рассмотренным задачам построения зависимостей. Другой подход основывается на решении несовместных систем неравенств и методах распознания образов. Указанные методы освещаются в разделе 2.4 очерка 2.

На основе рассмотренных подходов можно решать задачи определения зависимостей выходных эффектов исследуемого объекта от действующих факторов с учетом дополнительной информации о частных аспектах функциональных свойств объекта. В результате будет построена комплексная эмпирическая модель объекта, отражающая его в многообразии аспектов. Построение подобных моделей является искусством, основанным на знании содержательных предметных теорий и формальных методов планирования экспериментов.

3.5.5. Идентификация в противоречивых условиях

266

330. Модели объектов управления служат для прогнозирования их поведения с целью выработки управляющих решений. Для сложных задач управления характерным является неопределенность знаний об управляемых объектах, определяемая ограниченностью располагаемой информацией и динамикой развития как самого объекта, так и процесса его познания. Одним из подходов к решению задачи идентификации в данных условиях является метод самоорганизации моделей на основе решения систем несовместных взвешенных неравенств.

340. Рассмотрим более подробно указанный метод решения задачи. Предположим, что в результате наблюдений за эволюцией объекта либо в

результате процесса его познания можно сформулировать систему несовместных взвешенных неравенств

где {x , y : It } – множество эмпирических наблюдений зависимости F , It – множество значений индекса эмпирических наблюдений на текущий

в противном случае).

Критерий (5.2) достигает максимума на максимально совместной подсистеме системы неравенств (5.1), которая обладает максимальным суммарным весом. Веса неравенств назначаются исходя из предпочтений выполнения того или иного неравенства. В динамическом случае предпочтением обладают более поздние данные по сравнению с более ранними, что отражает процесс «старения» данных. Кроме того, на вес предпочтений может влиять степень достоверности данных и др. Веса должны быть положительно определенными и могут быть нормированными:

Таким образом, величина критерия (5.2) определяет взвешенное число выполненных неравенств и характеризует точность решения задачи аппроксимации исследуемой зависимости.

350. Поставленная задача относится к классу математических задач непрерывно-дискретного программирования. Алгоритм решения задачи

267

состоит из двух частей. Переборная часть алгоритма формирует всевозможные наборы значений характеристических функций , при этом

каждому k-му набору соответствует ожидаемое значение критерия Ckож .

Решающая часть алгоритма осуществляет методом наименьших квадратов решение соответствующего k-го набора неравенств по критерию

R

регуляризации.

В результате решения задачи (5.3) тем или иным методом будут получены зависимости

у F[ak ](x) ,

для которых можно оценить в какой степени выполняются заданные неравенства (5.1). В итоге могут быть вычислены реально достигнутые значения Ckр критерия (5.2). Знание реально достигнутого значения Ckр

позволяет сократить число вариантов решения задачи. Варианты, для которых ожидаемое значение критерия Ckож меньше или равно достигнутому

значению Ckр признаются неперспективными и удаляются из рассмотрения. Перспективные варианты удовлетворяют условию Ckож Сkр . Оптимальное

решение находится в итоге рассмотрения всех перспективных вариантов. Более подробно процедуры решения подобных задач приведены в разделе

2.4 очерка 2.

Полученное решение в общем случае носит локальный характер, так как построенная эмпирическая зависимость будет охватывать с заданной точностью лишь часть эмпирических данных. Поэтому необходимо провести дополнительные исследования. С этой целью распределение весов эмпирических данных в постановке задачи (5.1), (5.2) изменяется таким образом, что данным, которые не были охвачены ранее полученной зависимостью, присваивается максимальный вес, соответственно данным, которые уже были охвачены предыдущей зависимостью, присваивается минимальный вес. Решение задачи с перераспределенными весами позволит получить дополнительную зависимость, которая будет охватывать дополнительную часть данных. Указанную процедуру решения задачи можно продолжить итеративно до тех пор, пока на основе полученных частных решений не будет обеспечен полный охват всех эмпирических данных.

В результате описанной процедуры будет получено множество частных решений Fk , которые носят локальный характер. Локальный характер

частных решений Fk состоит в том, что они справедливы в локальных областях допустимых значений входных параметров k {x }k , которые

268

можно назвать областями компетенции зависимостей Fk . Глобальное

решение может быть получено, например, как объединение всех частных решений: 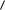{Fk }, { k }: k Ik 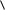. В общем случае логическое объединение

частных решений носит более сложный характер и согласно терминологии, принятой в данной работе, соответствует интеллектуальной операции синтеза конкретного.

360. При построении глобального решения необходимо обратить внимание, что среди эмпирических данных могут быть нерегулярные данные, представляющие собой случайные выбросы, недостоверные данные, ошибки и др. Для подобных данных необходимо либо найти скрытые факторы, которые обусловили соответствующие отклонения, либо удалить их из рассмотрения как статистические выбросы, снижающие точность представления регулярных данных.

3.5.6. Распознание ориентированных отношений

370. Характеристики объекта эмпирических исследований могут иметь такую степень неопределенности, которая не позволяет с заданной точностью построить его функциональную модель. В этих случаях одним из подходов является построение модели в виде ориентированного отношения.

Рассмотрим построение ориентированных отношений на основе эмпирических данных.

Предположим, что характеристики объекта исследования могут быть представлены ориентированным отношением

где x – вектор действующих факторов, y – выходной эффект.

Для выходного эффекта определены разряды качества, которые формально могут быть представлены в виде разбиения множества значений выходного эффекта на подмножества:

(6.2)

Здесь Yi – подмножество значений выходного эффекта, соответствующее

i-ому разряду качества.

Чтобы определить на основе вычислительной процедуры принадлежность конкретных значений вектора действующих факторов x образу i-го качества вводятся решающие правила

380. Методы построения эмпирических зависимостей, рассмотренные выше, основываются на одноуровневой постановке задач. Однако для действительно сложных систем одноуровневые постановки задач исследования являются недостаточными, так как во многих случаях они могут не отражать реальную сложность объекта исследования. Поэтому в настоящее время развиваются методы многоуровневой и более общей - сетевой постановки задач построения эмпирических зависимостей. Перспективными направлениями исследований в данном направлении являются методы группового учета аргументов (МГУА) 32 и искусственных нейронных сетей (НС), которые исторически сначала строились как аналоги биологических нейронных сетей, а в настоящее время представляют собой самостоятельные технические разработки. Рассмотрим последние методы более подробно. Изложение ведется в соответствии с работами 33.

390. Структура нейронных сетей

НС представляет собой «nараллельную, распределенную, адаптивную систему, которая восстанавливает скрытые закономерности и развивает свои способности по обработке информации в результате обучения».

Она обладает следующими отличительными особенностями:

-НС состоит из простых нейропроцессорных элементов (НЭ), или нейроэлементов;

-НЭ связаны между собой направленными информационными каналами (ИК), по которым распространяются информационные сигналы, закодированные в скалярной форме;

-каждый НЭ может быть связан посредством входных ИК с множеством других НЭ;

-каждый НЭ имеет единственный выходной ИК, который впоследствии может разветвляться;

-каждый НЭ может обладать собственной внутренней памятью (в основном в виде весовых параметров соединений) и может осуществлять локальную обработку приходящей к нему информации;

-обработка информации нейроэлементом осуществляется локально: она зависит только от значений, поступающих по входным ИК, и значений, хранящихся в его внутренней памяти.

В противоположность традиционным структурам обработки

32 Ивахненко, А.Г. Долгосрочное прогнозирование и управление сложными системами / А.Г. Ивахненко. – Киев: Техника, 1975.

33 Тимофеев, А.В. Нейросетевое представление неизвестных знаний и закономерностей / А.В. Тимофеев, А.А. Богданов, З.М. Шибзухов // Data Mining: учебный курс / В. Дюк, А. Самойленко. – СПб: Питер, 2001. – С.131–164.

Каллан, Р. Основные концепции нейронных сетей / Р. Каллан. -М.: Издательский дом "Вильямс", 2001.

271

информации, которые развиваются путем прямого программирования, НС развиваются и адаптируются в процессе обучения по примерам. Технология обучения подразделяется на две категории:

-обучение с учителем, при котором имеется множество примеров, для которых требуемый отклик или поведение НС известно;

-обучение без учителя, самообучение или самоорганизация, при котором процесс обучения НС происходит автономно: по мере поступления новой информации НС сама находит некоторые свойства и закономерности в данных.

400. Нейропроцессорные элементы

Каждый НЭ выполняет относительно простую функцию: получает информационные сигналы от других НЭ или внешних источников, формирует выходной информационный сигнал и передает его другим. Нейропроцессорные элементы соединяются между собой в нейронную сеть, имеющую в общем случае многослойный характер (рис. 3.5.3).

Внутри многослойной НС нейропроцессорные элементы подразделяются на три типа:

-входные, которые получают сигналы от внешних источников;

-промежуточные, которые принимают сигналы от одних НЭ, формируют сигналы и передают их другим;

-выходные, которые формируют выходные сигналы.

Промежуточные

сигналы

Рис. 3.5.3. Общая схема многослойной нейронной сети

272

Для описания функционирования НЭ в НС вводится ряд характеристик и правил (рис. 3.5.4).

Рис.3.5.4. Схема преобразования сигналов в НЭ

Особенности схемы (рис. 3.5.4) следующие:

- каждый j-й НЭ характеризуется скалярной величиной a j называемой активацией, которая соответствует уровню его активности;

-передача сигналов от одних НЭ к другим осуществляется посредством взвешенных соединений с настраиваемыми весовыми параметрами;

-каждое k -оe входное соединение характеризуется своей величиной вектора весов w jk ;

-взвешенное дендритное34 преобразование D w jk ; x jk определяет величину частной активации a jk , производимой k -ым соединением по

вектору x jk входных сигналов НЭ, участвующих в его образовании;

-правило суммирования активаций S(..., aik , ...) определяет

величину активации a j для j -го НЭ в зависимости от частных активаций a jk , производимых взвешенными соединениями, где индекс k пробегает

34 Греч. δένδρον - дерево (здесь в смысле древовидной структуры связей).

273