7 Задачі про максимальну течію і

МІНІМАЛЬНИЙ РОЗРІЗ У МЕРЕЖІ

7.1 Мета заняття

Ознайомлення c загальними мережними моделями дослідження задач обміну інформацією у комп’ютерних мережах, при плануванні постачання у транспортних мережах, розподілення матеріальних потоків та ін. Вивчення на практичних прикладах теореми та алгоритму Форда-Фалкерсона, який використовується для знаходження максимальної течії у мережах.

7.2 Методичні вказівки з організації самостійної роботи студентів

Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-8, 10-12] з таких питань: модель зваженого графу, кожній дузі якого приписана течія деякої речовини; задача про максимальну течію; теорема про максимальну течію і мінімальний розріз; теорема Форда-Фалкерсона; алгоритм Форда-Фалкерсона, його реалізація.

Підготовка і виконання практичного заняття проводиться за два етапи.

Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень: зважений граф; мережа; течія; пропускна здатність (місткість) дуги; джерело; стік; проміжний вузол; чиста течія; течія за дугою; переріз; пропускна здатність перерізу.

При виконанні першого етапу практичного заняття студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень.

Другий етап виконання практичного заняття пов’язаний з розв’язанням практичних завдань, які представлені у підрозділі 7.3, на основі запропонованих типових прикладів (див. підрозділ 7.4).

7.3 Контрольні запитання і завдання

7.3.1 Контрольні запитання

1. Який граф називається мережею?

2. Поясніть поняття «пропускна здатність (місткість) дуги графа».

3. Що являє собою течія у мережі?

4. Як можна зобразити течії у неорієнтованих графах?

5. Які вершини називаються джерелом, стоком, проміжними вершинами?

6. Надайте загальну постановку задачі про максимальну течію.

7. Охарактеризуйте використання теореми про максимальну течію і мінімальний розріз.

8. Для розв’язання яких задач використовується алгоритм Форда-Фалкерсона?

7.3.2 Контрольні завдання

Завдання 1. Найти максимальну течію для транспортної мережі , яка зображена на рис. 7.1. Кожній дузі транспортної мережі приписана пропускна здатність дуги.

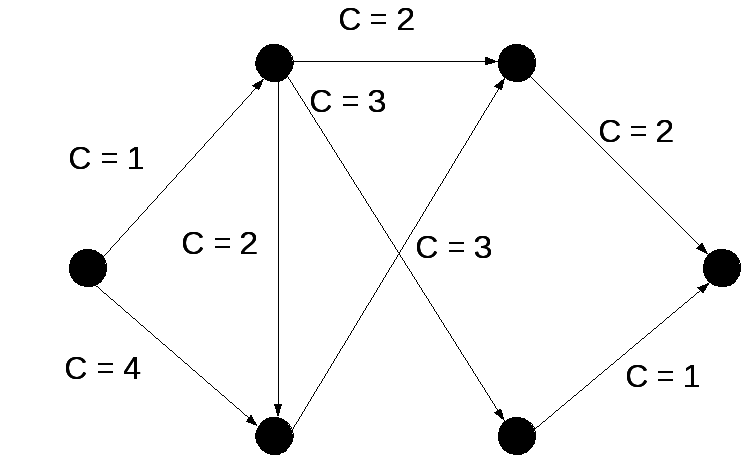
Рисунок 7.1 – Транспортна мережа

Завдання 2. Найти максимальну течію, яка може протікати у мережі (рис 7.2) з вузла у вузол. На рис. 7.2 для кожної дуги задається її пропускназдатність.

Рисунок 7.2 – Транспортна мережа

Завдання 3. Знайти максимальну течію, яка може протікати у мережі (рис 7.2) з вузла у вузол. Для кожної дуги задається така її пропускназдатність: ;;;;;;;.

Завдання 4. Визначити максимальний потік вантажу, який можна пропустити через транспортну мережу (з вузла у вузол) із заданими пропускнимиздатністями дуг (див. рис. 7.3).

Рисунок 7.3 – Транспортна мережа

Завдання 5. Визначити максимальну течію природного газу, який можна пропустити через ділянку магістрального газопроводу (з вузла у вузол), якщо структура ділянки магістрального газопроводу та пропускніздатністі дуг мережі цієї ділянки мають вигляд, який надається на рис. 7.4.

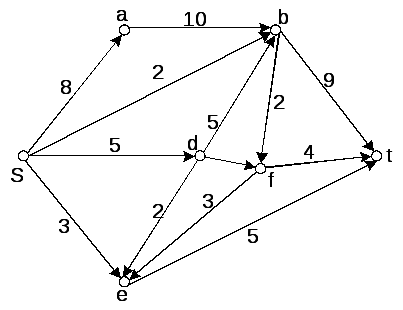
Рисунок 7.4 – Структура ділянки магістрального газопроводу

7.4 Приклади аудиторних і домашніх завдань

Завдання 1. Знайти максимальну течію в транспортній мережі , яка зображена на рис.7.5.

Рисунок 7.5 – Транспортна мережа

Розв’язок. Для знаходження максимальної течії скористаємося алгоритмом Форда-Фалкерсона. Знайдемо сумарну пропускну здатність дуг , що виходять із джерела (вершина 1) і сумарну пропускну здатність дуг, що входять у стік (вершина 14). Вони дорівнюютьі. Виходить, що максимальна течія у цій мережі не може бути більш, ніж 31.

Далі довільним способом розбиваємо мережу на прості непересічні ланцюги (ітерація 1). У цьому випадку зручно зробити це таким чином (див. рис. 7.6): ланцюг 1: (1, 2, 6, 10, 14); ланцюг 2: (1, 3, 7, 11, 14); ланцюг 3: (1, 4, 8, 12, 14); ланцюг 4: (1, 5, 9, 13, 14).

Рисунок 7.6 – Перша ітерація

Для кожного з ланцюгів знаходимо максимальну течію, виходячи із пропускних здатностей дуг. Наприклад, у першому ланцюзі – (1, 2, 6, 10, 14) – мінімальною пропускною здатністю є здатність дуги (2,6). Вона дорівнює 6, тому течія за цією дугою не може перевищувати 6.

На рис. 7.6 показана мережа, у якій позначені прості ланцюги, а поруч із пропускними здатностями дуг позначене значення течії. Дуги, у яких пропускна здатність дорівнює течії, називаються насиченими.

На першій ітерації одержуємо сумарну течію: 6+5+6+4=21.

На наступних ітераціях будемо намагатися збільшити величину течії.

Для цього вибираємо інші ланцюги, у яких немає насичених дуг.

На рис. 7.7–7.9 зображені наступні ітерації. Над дугою поруч із пропускними здатностями дуг через «;» позначаємо нове значення течії.

Розглянемо другу ітерацію (рис. 7.7). Вибираємо ланцюг, за яким можна збільшити течію. Це ланцюг (1, 2, 3, 6, 10, 14). Течію можна збільшити на 1, тому що пропускна здатність дуги (6, 10) дорівнює 7.

На другій ітерації течія збільшилася на 1 і дорівнює 22.

Рисунок 7.7 – Друга ітерація

Розглянемо третю ітерацію (рис. 7.8). Вибираємо ланцюг (1, 3, 8, 7, 10, 14). За цією дугою можна пропустити течію величиною 2, тому що пропускна здатність дуги (3,8) дорівнює 2. Одержуємо сумарну течію, яка дорівнює 22+2=24. На рис. 7.8 зображена мережа з течією, яка дорівнює 24.

Рисунок 7.8 – Третя ітерація

Розглянемо четверту ітерацію (рис. 7.9). Вибираємо ланцюг . За цією дугою можна пропустити течію величиною 1, тому що пропускна здатність дуги (9, 13) дорівнює 5. Одержуємо сумарну течію, яка дорівнює 24+1=25. На рис. 7.9 зображена мережа з течією, яка дорівнює 25.

Максимальна течія в транспортній мережі дорівнює 25.

Рисунок 7.9 – Четверта ітерація

Завдання 2. Нехай задається транспортна мережа , що складається з п’яти вузлів і восьми дуг, в якій розглядається течія з до(рис. 7.10). Кожній дузі приписані два числа: перше – величина течії за дугою, друга – пропускна здатність дуги. Знайти максимальну течію в цій мережі.

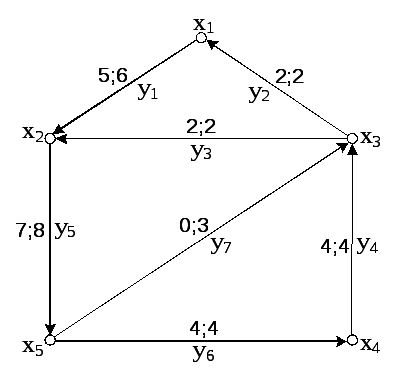
Рисунок 7.10 – Транспортна мережа

Розв’язок.

Визначимо чисту течію з кожної вершини :;;;;.

Течія з довеличини 3 є течія величини –3 здо.

Використаємо алгоритм Форда-Фалкерсона для розрахунку максимальної течії в мережі .

Крок 1. Візьмемо течію, що зображена на рис. 7.10 як початкова припустима течія. Вона має величину 3.

Крок 2. Привласнимо джерелу (вершині ) позначку (). Вершинапозначена, але не переглянута.

Крок 3. Переглянемо вершини, суміжні з вершиною . Вершиніпривласнимо позначку (+, 1), а вершині– позначку (). Течія за дугоюдорівнює, течія за дугою. Вершинапозначена і переглянута, а вершиниіпозначені, але не переглянуті.

Крок 4. Переглянемо вершини, суміжні з вершиною . Із вершин, суміжних з вершиною, не позначені вершиниі. Вершиніпривласнимо позначку (), оскількиі. Вершинуне позначаємо, оскільки.

Крок 5. Переглянемо вершини, суміжні з вершиною . Вершиніпривласнимо позначку (), оскільки. Стік позначений. Переходимо до операції збільшення течії.

Крок 6. Стік має позначку (), тому збільшуємо течію вздовж дугина 1.

Крок 7. Вершина має позначку (), тому збільшуємо течію вздовж дугина 1. Одержуємо нову течію величини 4 (див. рис. 7.11 а)).

а) течія величини 4; б) максимальна течія (величини 6)

Рисунок 7.11

Крок 8. Стираємо всі позначки.

Крок 9. Привласнимо вершині позначку ().

Крок 10. Переглянемо вершини, суміжні з вершиною . Вершиніпривласнимо позначку (). Вершинуне позначаємо, оскільки.

Крок 11. Переглянемо вершини, суміжні з вершиною . Вершиніпривласнимо позначку (), оскільки,і.

Крок 12. Переглянемо вершини, суміжні з вершиною . Вершиніпривласнимо позначку (–), оскільки,і. Стік позначений. Переходимо до операції збільшення течії.

Крок 13. Стік має позначку (–), тому зменшуємо течію вздовж дугина 2.

Крок 14. Вершина має позначку (), тому зменшуємо течію вздовж дугина 2.

Крок 15. Вершина має позначку (), тому зменшуємо течію вздовж дугина 2. Одержуємо нову течію величини 6 (див. рис. 7.11 б)).

Ця течія є максимальною. Це виходить з теореми [1]: для будь-якої мережі максимальна величина течії з (у нашому прикладі) до(у нашому прикладі) дорівнює мінімальній пропускній здатності перерізу, що відокремлюєвід.

Перевіримо це.

Крок 16. Стираємо всі позначки.

Крок 17. Привласнимо вершині позначку ().

Крок 18. Вершини, суміжні вершині , не можна позначити, оскільки дуганасичена –, а через дугутечія не передається. Стік залишився непозначеним. Отже, одержана течія є максимальною. Дугиіутворюють мінімальний переріз. Множина позначених вершин утворює той його бік, який містить джерело. Непозначені вершини утворюють інший бік перерізу, що містить стік.

Побудована течія має вигляд .

ПЕРЕЛІК ПОСИЛАНЬ

1. Бондаренко, М. Ф. Компьютерная дискретная математика [Текст] : учебник для вузов / М. Ф. Бондаренко, Н. В. Белоус, А. Г. Руткас. – Харьков: «Компания СМИТ», 2004. – 480 с.

2. Тевяшев, А. Д. Основы дискретной математики в примерах и задачах [Текст] : учеб. пособие для вузов / А. Д. Тевяшев, И. Г. Гусарова. – Харьков: ХНУРЭ, 2003. – 272 с.

3. Бардачов, Ю. М. Дискретна математика [Текст] : підручник / Ю.М. Бардачов, Н.А. Соколова, В.Є. Ходаков; За ред. В.Є. Ходакова. – К.: Вища шк., 2002. – 287 с.

4. Сигорский, В. П. Математический аппарат инженера [Текст] / В. П. Сигорский. – Киев: Техніка, 1977. – 768 с.

5. Капитонова, Ю. В. Лекции по дискретной математике [Текст] / Ю. В. Капитонова, С. Л. Кривой, А. А. Летичевский, Г. М. Луцкий. – СПб.: БХВ-Петербург, 2004. – 624 с.

6. Андерсон, Дж. А Дискретная математика и комбинаторика [Текст] / Джеймс А Андерсон. – М.: Издательский дом «Вильямс», 2003. – 960 с.

7. Бондаренко, М. Ф. Збірник тестових завдань з дискретної математики [Текст] / М. Ф. Бондаренко, Н. В. Білоус, І. Ю. Шубін. – Харків: ХТУРЕ, 2000. – 156 с.

8. Новиков, Ф. А. Дискретная математика для программистов [Текст] / Ф. А. Новиков. – СПб: Питер, 2001. – 304 с.

9. Виленкин, Н.Я. Комбинаторика [Текст] / Н. Я. Виленкин. – М.: Наука, 1969. – 328 с.

10. Конспект лекцій з дисципліни «Дискретна математика» для студентів усіх форм навчання напряму 6.050101  Комп’ютерні науки [Електронне видання] / Упоряд.: Н.В. Васильцова, Л.Е. Чала  Харків: ХНУРЕ, 2013. – 293 с.

11. Методичні вказівки до практичних робіт з дисципліни «Дискретна математика» (Частина 1) для студентів усіх форм навчання напряму 6.050101 – Комп’ютерні науки / Упоряд. Н. В. Васильцова, Л.Е. Чала – Харків: ХНУРЕ, 2012. – 68 с.

12. Методичні вказівки до самостійної роботи з дисципліни «Дискретна математика» для студентів усіх форм навчання напряму 6.050101  Комп’ютерні науки [Електронне видання] / Упоряд.: Н.В. Васильцова, Л.Е. Чала  Харків: ХНУРЕ, 2013.

Навчальне видання

МЕТОДИЧНІ ВКАЗІВКИ

до практичних занять з дисципліни

«ДИСКРЕТНА МАТЕМАТИКА»

(Частина 2)

для студентів усіх форм навчання напряму 6.050101 – Комп’ютерні науки

Упорядники: ВАСИЛЬЦОВА Наталія Володимирівна

ЧАЛА Лариса Ернестівна

Відповідальний випусковий В.М. Левикін

Редактор

Комп’ютерна верстка

План 2014 (друге півріччя), поз.

Підп. до друку Формат 60х84 1/16 Спосіб друку – ризографія

Умов.друк.арк. Облік.вид.арк. Тираж прим.

Зам. № Ціна договірна

ХНУРЕ. Україна, 61166, Харків просп. Леніна, 14

Віддруковано в навчально-науковому

Видавничо-поліграфічному центрі ХНУРЕ