
- •1 Множини. Алгебра множин
- •2 Відношення та операції над ними
- •3 Функціональні відношення
- •4 Булеві функції та перетворення
- •5 Нормальні форми зображення булевих функцій
- •6 Мінімізація булевих функцій
- •7 Функціональна повнота наборів булевих функцій
- •8 Логіка та обчислення висловлень
- •9 Логіка та обчислення предикатів
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ
МЕТОДИЧНІ ВКАЗІВКИ
до практичних занять з дисципліни
«ДИСКРЕТНА МАТЕМАТИКА»
(Частина 1)
для студентів усіх форм навчання
напряму 6.050101 – Комп’ютерні науки
ЗАТВЕРДЖЕНО
кафедрою Інформаційних управляючих систем.
Протокол № 4 від 10.11.11
Харків 2011
Методичні вказівки до практичних занять з дисципліни «Дискретна математика» (Частина 1) для студентів усіх форм навчання напряму 6.050101 – Комп’ютерні науки / Упоряд.: Н.В. Васильцова, Л.Е. Чала. – Харків: ХНУРЕ, 2011. – 68 с.
Упорядники: Н.В. Васильцова,
Л.Е. Чала
Рецензент В.О. Філатов, д.т.н., проф. кафедри ШІ
зміст
|
ВСТУП……………………………………………………………………….. |
5 |
|
1 МНОЖИНИ. АЛГЕБРА МНОЖИН……………………………………... |
6 |
|
1.1 Мета заняття……………………………………………………………... |
6 |
|
1.2 Методичні вказівки з організації самостійної роботи студентів……... |
6 |
|
1.3 Контрольні запитання і завдання………………………………………. |
7 |
|
1.3.1 Контрольні запитання…………………………………………………. |
7 |
|
1.3.2 Контрольні завдання………………………………………………….. |
8 |
|
1.4 Приклади аудиторних і домашніх задач………………………………. |
9 |
|
2 ВІДНОШЕННЯ ТА ОПЕРАЦІЇ НАД НИМИ…………………………… |
14 |
|
2.1 Мета заняття……………………………………………………………... |
14 |
|
2.2 Методичні вказівки з організації самостійної роботи студентів……... |
14 |
|
2.3 Контрольні запитання і завдання………………………………………. |
15 |
|
2.3.1 Контрольні запитання…………………………………………………. |
15 |
|
2.3.2 Контрольні завдання………………………………………………….. |
16 |
|
2.4 Приклади аудиторних і домашніх задач………………………………. |
19 |
|
3 ФУНКЦІОНАЛЬНІ ВІДНОШЕННЯ ……………………………………. |
23 |
|
3.1 Мета заняття……………………………………………………………... |
23 |
|
3.2 Методичні вказівки з організації самостійної роботи студентів……... |
23 |
|
3.3 Контрольні запитання і завдання………………………………………. |
23 |
|
3.3.1 Контрольні запитання…………………………………………………. |
23 |
|
3.3.2 Контрольні завдання………………………………………………….. |
24 |
|
3.4 Приклади аудиторних і домашніх задач………………………………. |
25 |
|
4 БУЛЕВІ ФУНКЦІЇ ТА ПЕРЕТВОРЕННЯ………………………………. |
26 |
|
4.1 Мета заняття……………………………………………………………... |
26 |
|
4.2 Методичні вказівки з організації самостійної роботи студентів……... |
26 |
|
4.3 Контрольні запитання і завдання………………………………………. |
27 |
|
4.3.1 Контрольні запитання…………………………………………………. |
27 |
|
4.3.2 Контрольні завдання………………………………………………….. |
28 |
|
4.4 Приклади аудиторних і домашніх задач………………………………. |
29 |
|
5 НОРМАЛЬНІ ФОРМИ ЗОБРАЖЕННЯ БУЛЕВИХ ФУНКЦІЙ………. |
34 |
|
5.1 Мета заняття……………………………………………………………... |
34 |
|
5.2 Методичні вказівки з організації самостійної роботи студентів……... |
34 |
|
5.3 Контрольні запитання і завдання………………………………………. |
34 |
|
5.3.1 Контрольні запитання…………………………………………………. |
34 |
|
5.3.2 Контрольні завдання………………………………………………….. |
35 |
|
5.4 Приклади аудиторних і домашніх задач………………………………. |
36 |
|
6 МІНІМІЗАЦІЯ БУЛЕВИХ ФУНКЦІЙ…………………………………... |
40 |
|
6.1 Мета заняття……………………………………………………………... |
40 |
|
6.2 Методичні вказівки з організації самостійної роботи студентів……... |
40 |
|
6.3 Контрольні запитання і завдання………………………………………. |
41 |
|
6.3.1 Контрольні запитання…………………………………………………. |
41 |
|
6.3.2 Контрольні завдання………………………………………………….. |
41 |
|
6.4 Приклади аудиторних і домашніх задач………………………………. |
44 |
|
7 ФУНКЦІОНАЛЬНА ПОВНОТА НАБОРІВ БУЛЕВИХ ФУНКЦІЙ…... |
47 |
|
7.1 Мета заняття……………………………………………………………... |
47 |
|
7.2 Методичні вказівки з організації самостійної роботи студентів……... |
47 |
|
7.3 Контрольні запитання і завдання………………………………………. |
48 |
|
7.3.1 Контрольні запитання…………………………………………………. |
48 |
|
7.3.2 Контрольні завдання………………………………………………….. |
48 |
|
7.4 Приклади аудиторних і домашніх задач………………………………. |
49 |
|
8 ЛОГІКА ТА ОБЧИСЛЕННЯ ВИСЛОВЛЕНЬ…………………………… |
53 |
|
8.1 Мета заняття……………………………………………………………... |
53 |
|
8.2 Методичні вказівки з організації самостійної роботи студентів……... |
53 |
|
8.3 Контрольні запитання і завдання………………………………………. |
54 |
|
8.3.1 Контрольні запитання…………………………………………………. |
54 |
|
8.3.2 Контрольні завдання………………………………………………….. |
55 |
|
8.4 Приклади аудиторних і домашніх задач………………………………. |
57 |
|
9 ЛОГІКА ТА ОБЧИСЛЕННЯ ПРЕДИКАТІВ……………………………. |
61 |
|
9.1 Мета заняття……………………………………………………………... |
61 |
|
9.2 Методичні вказівки з організації самостійної роботи студентів……... |
61 |
|
9.3 Контрольні запитання і завдання………………………………………. |
62 |
|
9.3.1 Контрольні запитання…………………………………………………. |
62 |
|
9.3.2 Контрольні завдання………………………………………………….. |
62 |
|
9.4 Приклади аудиторних і домашніх задач………………………………. |
64 |
|
ПЕРЕЛІК ПОСИЛАНЬ……………………………………………………… |
67 |
ВСТУП
Дисципліна «Дискретна математика» входить до складу дисциплін циклу природничо-наукової підготовки бакалаврів з напряму 6.050101 – «Комп’ютерні науки» і є однією з базових математичних дисциплін цього циклу.
Матеріал, який пропонується для вивчення першої частини дисципліни, складається з таких розділів: «Основи теорії множин»; «Відношення та їх властивості»; «Булева алгебра»; «Елементи математичної логіки («Логіка та обчислення висловлень», «Логіка та обчислення предикатів)».
Добір і викладення практичного матеріалу цих розділів дисципліни виконано з урахуванням вимог фундаментальної освіти з комп’ютерних наук, інформаційних технологій, сучасних інженерних і соціально-економічних напрямків з високим рівнем автоматизації та комп’ютеризації.
Методичні вказівки призначені для студентів молодших курсів, які спеціалізуються в області комп’ютерних наук і зобов’язані використовувати отримані практичні знання і навички при проектуванні та упровадженні інформаційно-управляючих систем і систем штучного інтелекту. Однак практичний матеріал з дисципліни «Дискретна математика» буде також корисним для тих, хто намагається підвищити кваліфікацію в напрямках (розділах дисципліни), що перелічені вище.
Для вивчення першої частини дисципліни «Дискретна математика» студент повинен мати знання математики в обсязі середньої школи і деякі основні поняття з розділів дисципліни з вищої математики.
У методичні вказівки з дисципліни «Дискретная математика» входить перелік литератури (підручники, навчальні посібники і монографії), яку можна використовувати для уточнювання матералу або, за бажанням, для більш глибокого вивчення деяких теоретичних положень і практичних прикладів.
1 Множини. Алгебра множин
1.1 Мета заняття
Ознайомлення на практичних прикладах з основними поняттями теорії множин. Вивчення способів задання множин і способів визначення множин за допомогою операцій над деякими іншими множинами. Вивчення інструментів наочного подання відношень між множинами. Аналіз формул і тотожностей, які виражають властивості операцій алгебри множин. Вивчення і використання методів доведення тотожностей алгебри множин.
1.2 Методичні вказівки з організації самостійної роботи студентів
Під час підготовки до практичного заняття необхідно повторити лекційний матеріал, розділи літератури [1-10] з таких питань: інтуїтивне поняття множини (кантеровська теорія множин, її парадокси); скінченні й нескінченні множини; універсальна і порожня множини; способи задання множин; множина і підмножини, булеан множини; геометрична інтерпретація множин (круги Ейлера і діаграми Венна); операції на множинах; загальне визначення алгебри, поняття алгебри множин; аксіоми алгебри множин; тотожні перетворення формул алгебри множин.
Підготовка і виконання практичного заняття проводиться у два етапи. Перший етап пов’язаний з вивченням на практичних прикладах наступних основних понять і визначень теорії множин: множина, елемент множини, клас (сімейство), мультимножина, упорядкована множина, кортеж, довжина (розмірність) кортежу, скінченні, нескінченні, зчисленні множини, порожня множина, універсальна множина (універсум), способи задання множин, потужність множини, рівнопотужні множини, рекурсивно задана множина, підмножина, відношення приналежності і включення, властива і невластива підмножини, булеан множини, (множина-степень), теоретико-множинні операції на множинах, об’єднання множин, перетин множин, розбиття множини, різниця множин, доповнення (заперечення) множини, диз’юнктивна сума (симетрична різниця), геометричне подання множин і операцій над ними, загальне поняття алгебри, носій алгебри, сигнатура, бінарна та унарна операції, алгебра множин, закони алгебри множин, двоїсті символи.
При виконанні першого етапу студент повинен запропонувати і записати індивідуальний приклад для кожного з розглянутих вище понять і визначень.
Другий етап виконання практичного заняття пов’язаний з вирішенням практичних завдань, представлених у підрозділі 1.3, на основі запропонованих типових прикладів (див. підрозділ 1.4).
1.3 Контрольні запитання і завдання
1.3.1 Контрольні запитання
Що таке множина? Наведіть приклади різних множин.
Які способи задання множин Ви знаєте?
Що таке порожня множина? Обґрунтуйте необхідність використання порожньої множини.
Що таке універсальна множина? Наведіть приклади універсальних множин.
Дайте визначення скінченної і нескінченної множини.
Дайте визначення счисленної множини.
Що таке потужність множини?
Дайте визначення підмножини. Наведіть приклади підмножин.
Яке відношення між множинами називають строгим включенням, а яке нестрогим включенням?
Чим відрізняється поняття включення (
 або
або )
від поняття приналежності (
)
від поняття приналежності ( )?
)?У яких випадках можна говорити, що множини
 ,
, і
і рівні?
рівні?Які операції над множинами дозволяють будувати нові множини, використовуючи вже існуючі?
Яка пріоритетність виконання операцій над множинами?
Які способи графічної ілюстрації операцій над множинами Ви знаєте?
Поясніть узагальнене поняття алгебри. Наведіть приклади алгебр.
Що таке алгебра множин?
Яка операція над множинами називається бінарною?
Яка операція над множинами називається унарною?
Назвіть основні аксіоми (закони) алгебри множин.
Які властивості має порожня множина та універсальна множина?
Опишіть принцип двоїстості в алгебрі множин, наведіть приклади двоїстих символів.
Поясніть способи перетворення формул алгебри множин.
1.3.2 Контрольні завдання
Завдання 1.
Опишіть словами кожне із множин: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Завдання 2.
Перелічить елементи множини
![]() .
.
Завдання 3. Перелічить елементи множини
![]() .
.
Завдання 4.
Опишіть множину
![]() за допомогою характеристичної властивості.
за допомогою характеристичної властивості.
Завдання 5.
Перелічить підмножини множини
![]() .
.
Завдання 6.
Перелічить підмножини множини
![]() .
.
Завдання 7. Визначите кількість елементів у кожній множині:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г);
;
г);![]() ;
д)
;
д)![]() .
.
Завдання 8.
Нехай множина перших 20 натуральних
чисел
це універсум. Запишіть такі її підмножини:
![]() –
підмножина парних чисел;
–
підмножина парних чисел;![]() – підмножина непарних чисел;
– підмножина непарних чисел;![]() – підмножина квадратів чисел;
– підмножина квадратів чисел;![]() –
підмножина простих чисел.
–
підмножина простих чисел.
Завдання 9.
Чи рівні між собою множини
![]() і
і![]() (якщо ні, то чому?):
(якщо ні, то чому?):
а)
![]() ,
,![]() ;
;
б)
![]() ,
,![]() ;
;
в)
![]() ,
,![]() ;
;
г)
![]() ,
,![]() ;
;
д)
![]() ,
,![]() .
.
Завдання 10.
Доведіть, що
 ,
де
,
де![]() і
і![]() – множини.
– множини.
Завдання 11.
Нехай
![]() ,
,![]() ,
,![]() ,
а
,
а![]() .
Визначити множини: 1)
.
Визначити множини: 1)![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() ;
8)
;
8)![]() .
.
Завдання 12.
Чи існують такі множини
![]() ,
,![]() ,
,![]() ,
що
,
що![]() ,
,![]() ,
,![]() ?
?
Завдання 13.
Доведіть наступну рівність
![]() .
.
Завдання 14.
Доведіть рівність
![]() .
.
Завдання 15.
Доведіть за допомогою тотожних перетворень
співвідношення:
 ;
; .
Результат перевірте за допомогою діаграм
Ейлера-Венна.
.
Результат перевірте за допомогою діаграм
Ейлера-Венна.
Завдання 16.
У якому відношенні перебувають множини
![]() і
і![]() ,
якщо
,
якщо![]() ?
?
Завдання 17.
Покажіть справедливість тотожностей:
а)
![]() ;
б)
;
б)![]() .
.
Завдання 18.
Виходячи з відношення приналежності,
доведіть справедливість наступних
виразів: а)
 ;
б)
;
б) ;
в)
;
в) ; г)
; г) .
.
Завдання 19.
Використовуючи діаграми Эйлера-Венна,
покажіть рівность двох множин
![]() .
.
Завдання 20.
Для кожної з наведених нижче множин
використовуйте діаграму Ейлера-Венна
і заштрихуйте ті її частини, які зображують
задані множини: 1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)![]() ;
5)
;
5)![]() ;
6)
;
6)![]() ;
7)
;
7)![]() .
.
Завдання 21.
Знайдіть наступні множини: а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
1.4 Приклади аудиторних і домашніх завдань
Завдання 1.
Пояснити,
чому
![]() ,
а
,
а![]() .
.
Розв’язок.
Множина
![]() складається із чотирьох елементів,
одним із яких є 3, тому приналежність
даного елемента множині записується
як
складається із чотирьох елементів,
одним із яких є 3, тому приналежність
даного елемента множині записується
як![]() .
.
Множина
![]() складається із чотирьох елементів:
множини
складається із чотирьох елементів:
множини![]() ,
множини
,
множини![]() ,
об’єкта (елемента множини) 1 і об’єкта
(елемента множини) 2. У складі цих елементів
не існує множини
,
об’єкта (елемента множини) 1 і об’єкта
(елемента множини) 2. У складі цих елементів
не існує множини![]() ,
отже, співвідношення записується як
,
отже, співвідношення записується як![]() .
.
Завдання 2. Нехай
задана множина
![]() .
Описати цю множину за допомогою
характеристичної властивості.
.
Описати цю множину за допомогою
характеристичної властивості.
Розв’язок.
Множина
![]() за допомогою характеристичної властивості
записується так:
за допомогою характеристичної властивості
записується так:![]() .
.
Завдання 3.
Довести, що множини
![]() і
і![]() рівні між собою.
рівні між собою.
Доведення.
Дві множини
![]() і
і![]() рівні (тотожні) тоді й тільки тоді, коли
кожний елемент
рівні (тотожні) тоді й тільки тоді, коли
кожний елемент![]() є елементом
є елементом![]() і навпаки. Для даних множин ця умова
виконується, отже, вони рівні між собою,
тобто
і навпаки. Для даних множин ця умова
виконується, отже, вони рівні між собою,
тобто![]() .
.
Завдання 4. Довести, що порожня множина є підмножиною будь-якої множини.
Доведення.
Припустимо, що
існує множина
![]() така, що
така, що![]() .
Це означає, що в
.
Це означає, що в![]() є деякий елемент
є деякий елемент![]() ,
що не міститься в
,
що не міститься в![]() .
Але це неможливо, тому що
.
Але це неможливо, тому що![]() не містить жодного елемента.
не містить жодного елемента.
Завдання 5.
Нехай
![]() ,
,![]() .
Знайти
.
Знайти![]() ,
,![]() ,
,![]() ,
,![]() .
.
Розв’язок.
![]() ,
,
![]() ,
,![]() ,
,![]() .
.
Завдання 6.
Нехай
![]() ,
,![]() .
Довести, що
.
Довести, що![]() .
.
Розв’язок.
Крок 1. Покажемо,
що
![]() .
.
![]()
Крок 2. Покажемо,
що
![]() .
.
![]()
За результатами
виконання кроків 1 і 2 робимо висновок,
що
![]() .
.
Завдання 7.
Довести, що
 ,
де
,
де![]() і
і![]() множини.
множини.
Розв’язок.
Крок 1. Покажемо,
що
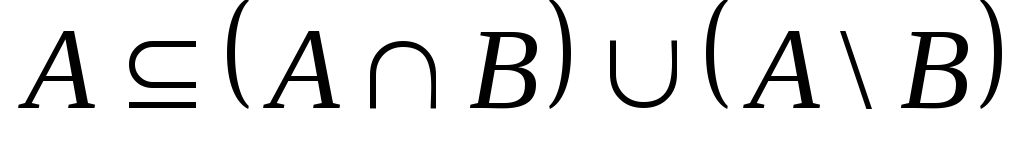
![]()

Крок 2. Покажемо,
що
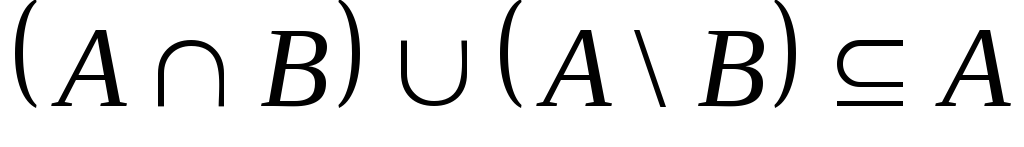
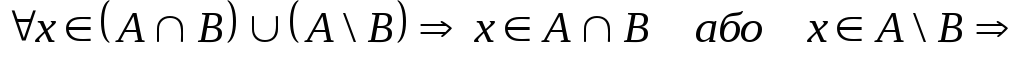
![]()

За результатами
виконання кроків 1 і 2 робимо висновок,
що
 .
.
Завдання 8.
Довести справедливість тотожності
![]() .
.
Доведення.
Нехай
![]() ,
тоді
,
тоді![]() або
або![]() .
Якщо
.
Якщо![]() ,
то
,
то![]() належить об’єднанню
належить об’єднанню![]() з будь-якою множиною, тобто
з будь-якою множиною, тобто![]() і
і![]() ,
отже,
,
отже,![]() є елементом перетину множин
є елементом перетину множин![]() і
і![]() ,
тобто
,
тобто![]() .
.
Якщо
![]() ,
то
,
то![]() і
і![]() ,
отже,
,
отже,![]() і
і![]() ,
тобто і у цьому випадку
,
тобто і у цьому випадку![]() є елементом перетину тих же множин.
є елементом перетину тих же множин.
Таким чином,
доведено
![]() .
Аналогічно доводиться і співвідношення
.
Аналогічно доводиться і співвідношення![]() .
Відповідно до визначення рівності
множин приходимо до необхідної тотожності
.
Відповідно до визначення рівності
множин приходимо до необхідної тотожності![]() .
.
Завдання 9.
Довести справедливість співвідношення
![]() .
.
Доведення.
Співвідношення
![]() доводиться наступними перетвореннями
з використанням тотожностей алгебри
множин:
доводиться наступними перетвореннями
з використанням тотожностей алгебри
множин:
![]() .
.
Завдання 10.
Указати всі
підмножини множини
![]() .
.
Розв’язок.
Кількість підмножин
обчислюється за формулою
![]() ,
де
,
де![]()
кількість елементів множини
кількість елементів множини
![]() ,
отже,
,
отже,![]() .
.
Перелічимо
підмножини множини
![]() :
:
![]() .
.
Завдання 11.
Зобразити
результат виконання операції
![]() ,
використовуючи діаграми Эйлера-Венна.
,
використовуючи діаграми Эйлера-Венна.
Розв’язок.
а) виконаємо
операцію
![]() і зобразимо її результат
і зобразимо її результат![]() на наступній
діаграмі (рис. 1.1).
на наступній
діаграмі (рис. 1.1).
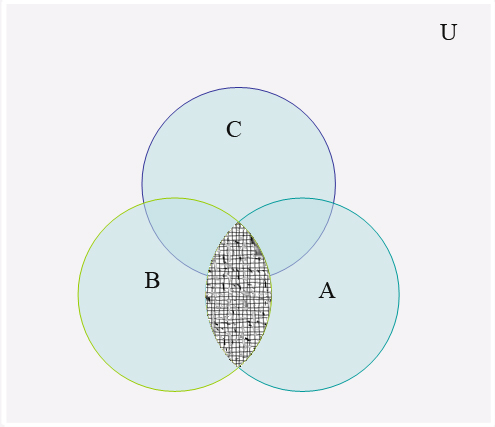
Рисунок 1.1
Операція
![]()
Множині
![]() буде відповідати зафарбована область
діаграми.
буде відповідати зафарбована область
діаграми.
б) виконаємо
операцію
![]() і зобразимо її результат
і зобразимо її результат![]() на наступній діаграмі (рис. 1.2).
на наступній діаграмі (рис. 1.2).
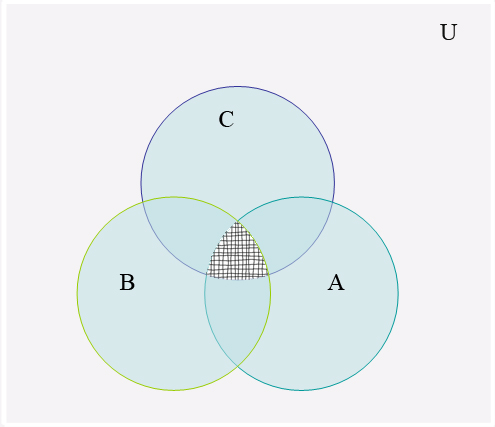
Рисунок 1.2
Операція
![]()
Множині
![]() буде відповідати зафарбована область
на даній діаграмі, що і є результатом
виконання операції
буде відповідати зафарбована область
на даній діаграмі, що і є результатом
виконання операції![]() .
.
Завдання 12.
Показати за
допомогою діаграм Эйлера-Венна, що
![]() .
.
Розв’язок.
Множина
![]() є доповненням множини
є доповненням множини![]() ,
яка представлена на рис. 1.3, тому
,
яка представлена на рис. 1.3, тому![]() зобразимо зафарбованою областю, показаною
на рис. 1.4.
зобразимо зафарбованою областю, показаною
на рис. 1.4.

Рисунок 1.3
Операція
![]()
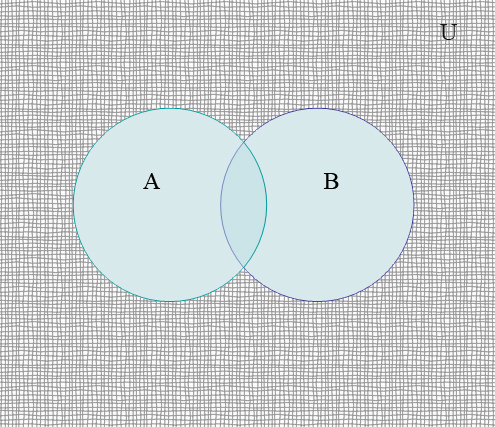
Рисунок 1.4
Операція
![]()
Множині
![]() і множині
і множині![]() відповідають зафарбовані області
діаграм Эйлера-Венна на рис. 1.5.
відповідають зафарбовані області
діаграм Эйлера-Венна на рис. 1.5.


а) операція
![]() б) операція
б) операція![]()
Рисунок 1.5
Операції
![]() і
і![]()
Множині
![]() відповідають ті частини, які зафарбовані
на обох попередніх діаграмах Эйлера-Венна,
тому на рис. 1.6 вона може бути зображена
таким чином:
відповідають ті частини, які зафарбовані
на обох попередніх діаграмах Эйлера-Венна,
тому на рис. 1.6 вона може бути зображена
таким чином:
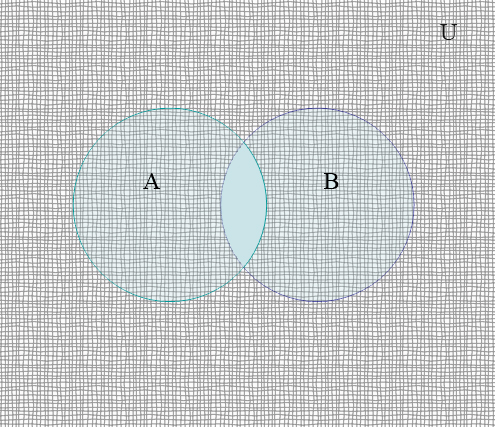
Рисунок 1.11
Операція
![]()
Показали, що і
множина
![]() ,
і множина
,
і множина![]() однаково зображуються на діаграмі
Эйлера-Венна, тому ці множини рівні,
тобто
однаково зображуються на діаграмі
Эйлера-Венна, тому ці множини рівні,
тобто![]() .
.
